Синус и косинус суммы и разности аргументов

1.

Синус и косинус суммы и разности
аргументов

2.

Повторение

3.

Алгоритм
1) Надо поставить знак, который имела бы первоначальная
функция (при условии, что t принадлежит первой четверти)
2) Выяснить, меняется ли функция на «кофункцию»
(“лошадиное правило”).
Основная ошибка: неправильно
поставленный знак. Поэтому лучше
начинать именно с него.
назад

4.

Вычислить с помощью формул приведения
Пример №1 cos 3300
cos 270
0
60
У
sin 60 0
0
Название
функции
меняем
Х
0
Ответ: cos 330
правило
3
2
270 0
+

5.

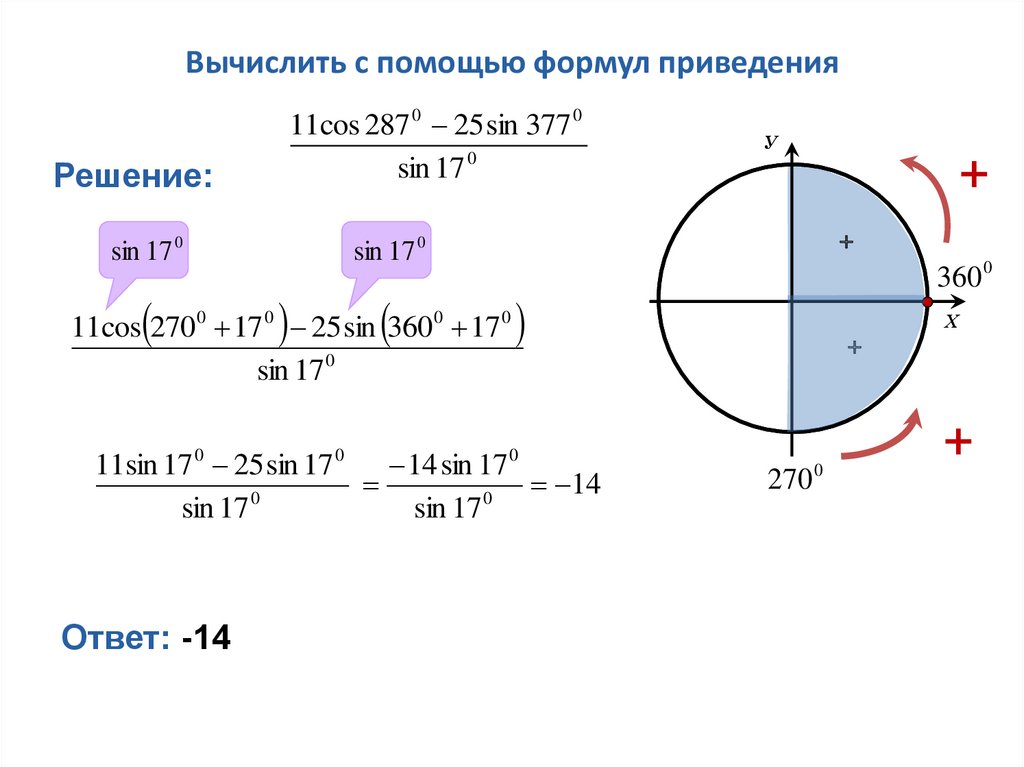
Вычислить с помощью формул приведения
11cos 287 0 25 sin 377 0
sin 17 0
Решение:
sin 17 0
У
sin 17 0
11cos 270 0 17 0 25 sin 3600 17 0
sin 17 0
Ответ: -14
0
360 0
11sin 17 25 sin 17
14 sin 17
14
0
0
sin 17
sin 17
0
+
0
270 0
Х
+

6.

синус и косинус суммы
аргументов
sin x y sin x cos y cos x sin y
cos x y cos x cos y sin x sin y
С их помощью можно вывести практически все
основные формулы тригонометрии

7.

синус и косинус разности
аргументов
Воспользуемся тем, что х – у = х + ( - у)
cos( y ) cos y
sin( y ) sin y
sin x ( y) sin x cos( y) cos x sin( y)
sin x y sin x cos y cos x sin y
cos( y ) cos y
sin( y ) sin y
cos x y cos x cos( y) +
sin x sin( y)
cos x y cos x cos y sin x sin y

8.

sin x y sin x cos y cos x sin y
Вычислить
sin 1050 sin( 600 450 ) sin 600 cos 450 cos 600 sin 450
3 2 1 2
2 2 2 2
6
2
4
4
6 2
4
cos x y cos x cos y sin x sin y
cos15 0 cos 450 300 cos 450 cos 300 sin 450 cos 300
6
2
3 2 1 2
4
4
2 2 2 2
6 2
4

9.

Формулы можно применять как слева направо, так и
справа налево
cos x y = cos x cos y sin x sin y
=
назад

10.

14
3
14
3
cos
sin
sin
Вычислить cos
15
5
15
5
Решение:
вспомним формулу
14 3
14
3
14
3
cos
cos
sin
sin
cos
5
15
15
5
15
5
14 9
5
1
cos
cos cos
15 15
15
3 2

11.

Вычислить
cos1250 cos 50 sin 550 cos 850
Заметим, что
1250 550 1800
и
125 180 55
0
cos 55
0
0
50 850 900
850 900 50
sin 50
0
cos(1800 550 ) cos 50 sin 550 cos(900 50 )
cos 550 cos 50 sin 550 sin 50
cos x cos y sin x sin y cos x y
(cos 550 cos 50 sin 550 sin 50 ) cos(550 50 )
1
cos 60
2
0