Similar presentations:
Тангенс суммы и разности аргументов
1. 1)Продолжите формулы:
a)b)
c)
d)
sin(x+y)=
cos(x-y)=
cos(x-y)=
sin(x-y)=
2. Проверь себя!
a)b)
c)
d)
sin(x+y)=sinx·cosy+cosy·sinx
cos(x-y)=cosx·cosy+sinx·siny
cos(x-y)=cosx·cosy+sinx·siny
sin(x-y)=sinx·cosy-cos·ysinx
1б
1б
1б
1б
3. Упростите:
а)cos a cos 3a-sin a sin Заб) sin 2а cos а + cos 2а sin а
в)sin а cos За + cos а sin За
г)cos а cos 2а + sin а sin 2а
4. Ответы:
a)cos 4а;Б)sin За;
в) sin 4а;
г) cos а.
1б
1б
1б
1б
5. Упростите:
а) sin 37° cos 8° + cos 37° sin 8°sin 30° cos 15° + sin 15° cos 30°
б) cos 20° cos 65° + sin 20° sin 65°
sin 75° cos 30° - sin 30° cos 75°
6. Проверь себя!
а) sin 37° cos 8° + cos 37° sin 8° = 1sin 30° cos 15° + sin 15° cos 30°
б) cos 20° cos 65° + sin 20° sin 65° =1
sin 75° cos 30° - sin 30° cos 75°
1б
1б
7. Тангенс суммы и разности аргументов
8. Цели
• Изучить формулы тангенса суммы иразности аргументов.
• Рассмотреть практическое
применение данных формул.
9.
Повторим1)Что такое тангенс?
2)Как он связан с синусом и
косинусом?
3)Можно ли вывести формулы
тангес суммы и разности
аргументов, зная формулы
суммы и разности аргументов
синуса и косинуса?
10.
Выведем формулу тангенса суммыдвух аргументов
tg x y
По определению тангенс есть отношение синуса
к косинусу одного и того же аргумента
sin x y
tg x y
cos x y
По изученным формулам синуса и
косинуса суммы, получим
11.
sin x ytg x y
cos x y
sin x cos y cos x sin y
,
cos x cos y sin x sin y
Разделим числитель и знаменатель
последней дроби на cos x cos y
cos x cos y 0
При всех допустимых значениях х и у
12.
sin x cos y cos x sin ycos x cos y sin x sin y
sin x cos y cos x sin y
cos x cos y cos x cos y
cos x cos y sin x sin y
cos x cos y cos x cos y
tgx tgy
.
1 tgx tgy
13.
Получили:tgx tgy
tg x y
1 tgx tgy
Аналогично можно доказать, что
tg(x-y)=
14.
Проверьте!tgx tgy
tg x y
1 tgx tgy
15.
Пример 1.Вычислить:
tg 75
0
Решение.
tg 45 tg30
tg75 tg 45 30
0
0
1 tg 45 tg30
3
1
3 3
3
3 3 3
1 1
3
0
0
0
0
0
16.
Пример 2.Вычислить:
0
tg15
Решение.
tg 45 tg30
tg15 tg 45 30
0
0
1 tg 45 tg30
3
1
3 3
3
3 3 3
1 1
3
0
0
0
0
0
17.
Пример 3.Вычислить:
Решение.
tg 27 tg18
0
0
1 tg 27 tg18
0
tg 27 tg18
0
0
tg 27 18
0
0
1 tg 27 tg18
0
0
tg 45 1
0
0










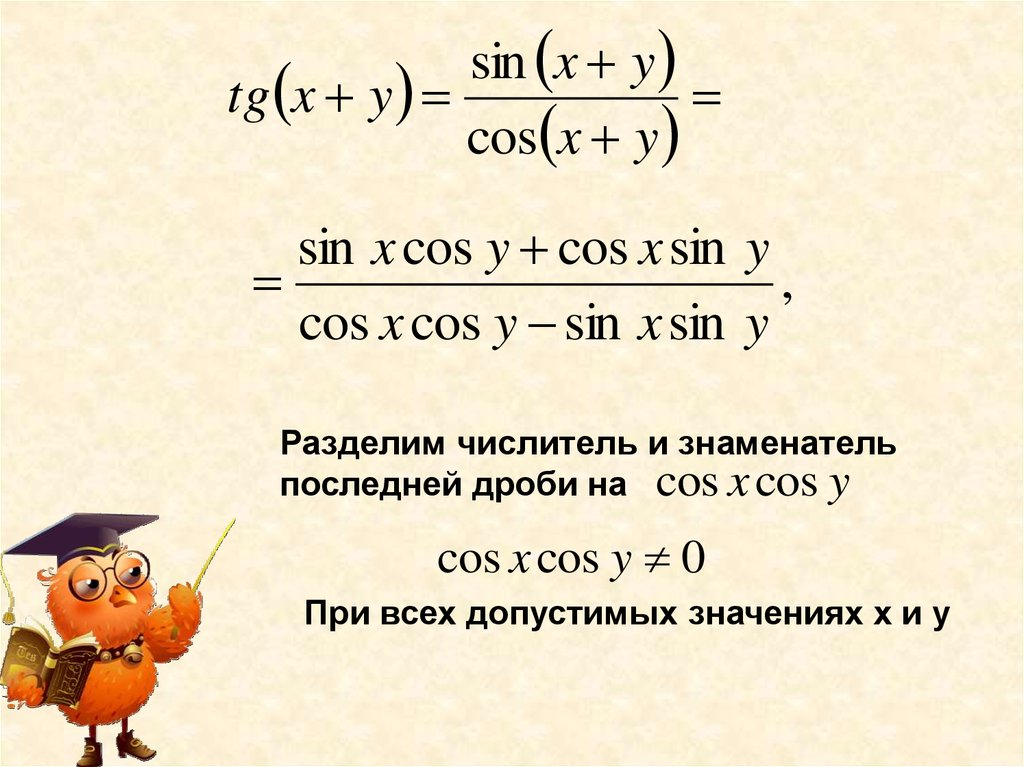
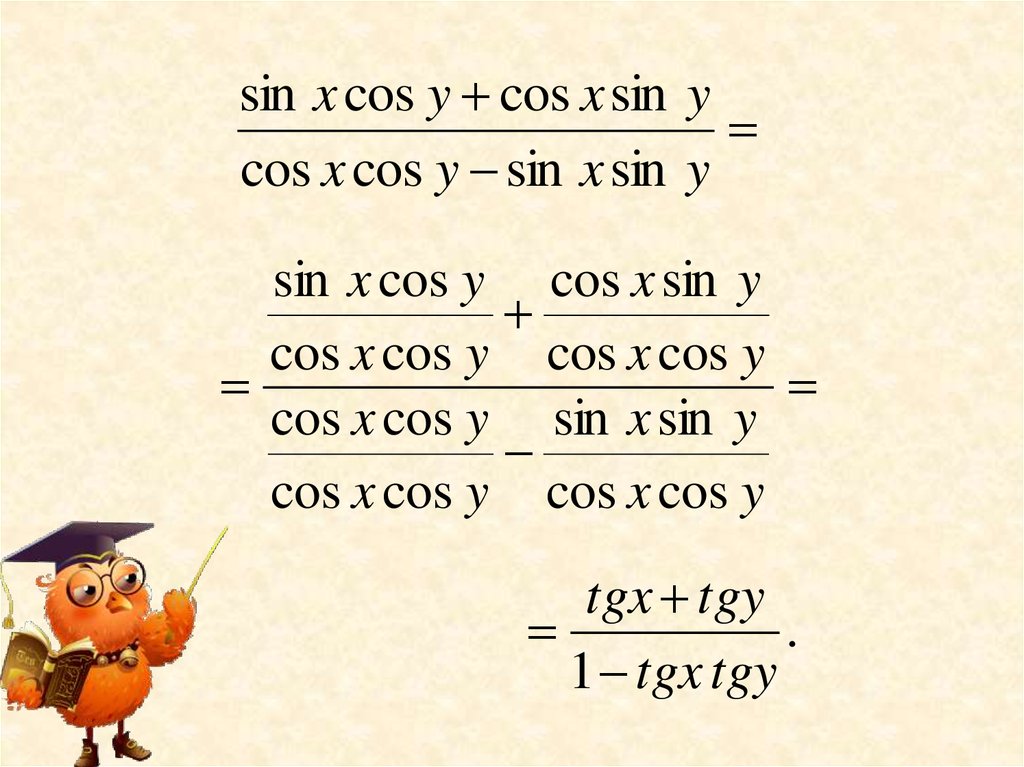

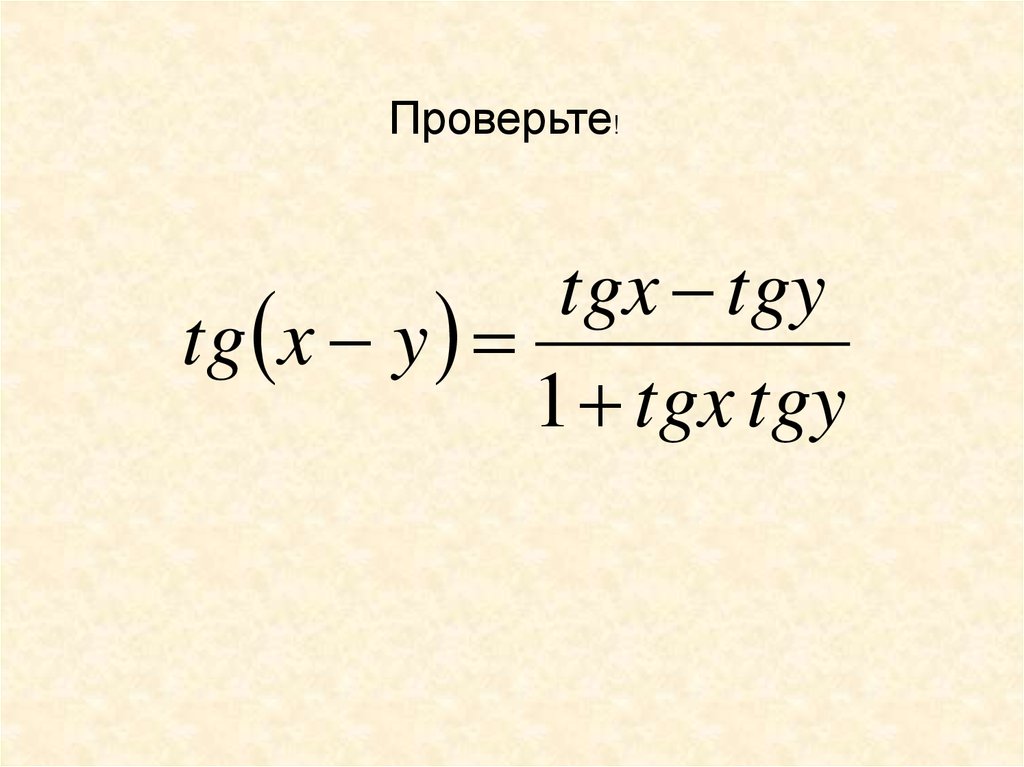
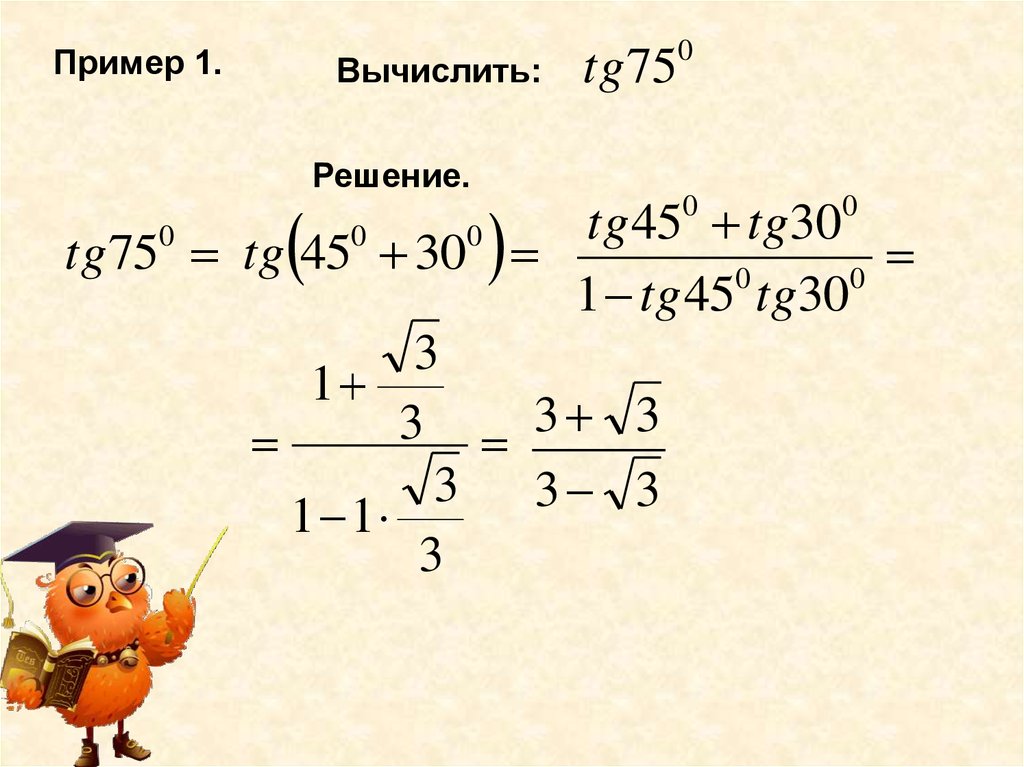
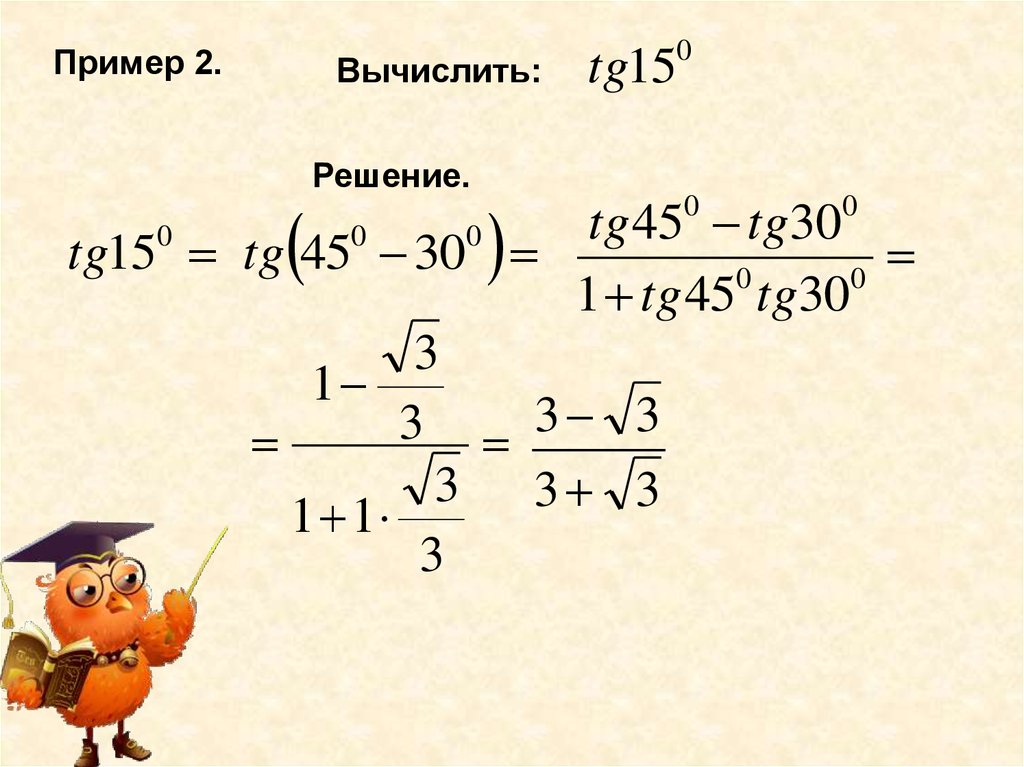

 mathematics
mathematics








