Similar presentations:
Применение формулы Пика для решения геометрических задач
1.
Исследовательская работапо математике
«Применение формулы Пика для
решения геометрических задач»
Выполнил: Загидуллин Риналь, ученик 9 класса
Руководитель: Ганеева А.М., учитель математики
2.
Задачи исследования:Подобрать и изучить соответствующую литературу;
рассмотреть вывод формулы Пика;
подобрать
класс задач, которые можно решить с помощью
формулы Пика и решить их;
проверить
целесообразность и эффективность применения
формулы Пика;
расширение кругозора;
сделать сравнительный анализ: какой из способов
наиболее
эффективный (традиционный или с помощью формулы?);
углубленное изучение школьного курса геометрии.
3.
Георг Алекса́ндр Пик австрийский математик.Родился в еврейской семье
10 августа 1859
Умер 26 июля 1942 года.
Мать — Йозефа Шляйзингер ,
отец — Адольф Йозеф Пик
4. СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ
1) Подсчет количества клеток;2) Применение формул планиметрии;
3) Разбиение фигуры на более простые
фигуры;
4) Достроение фигуры до прямоугольника;
5) Формула Пика.
5.
6.
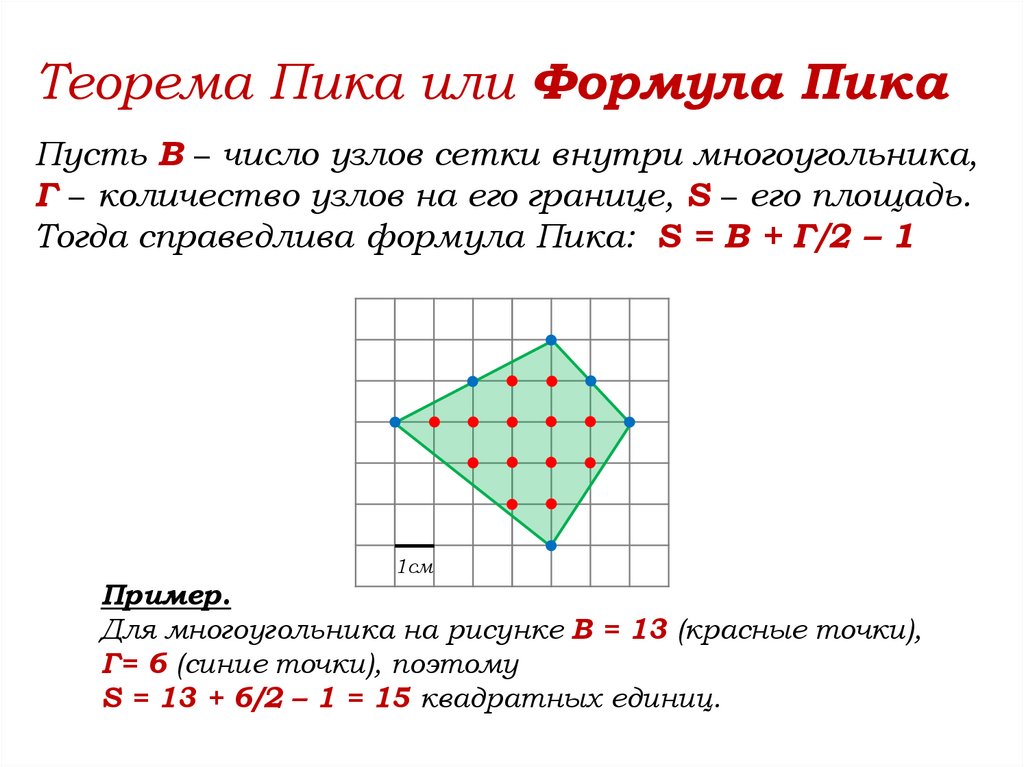
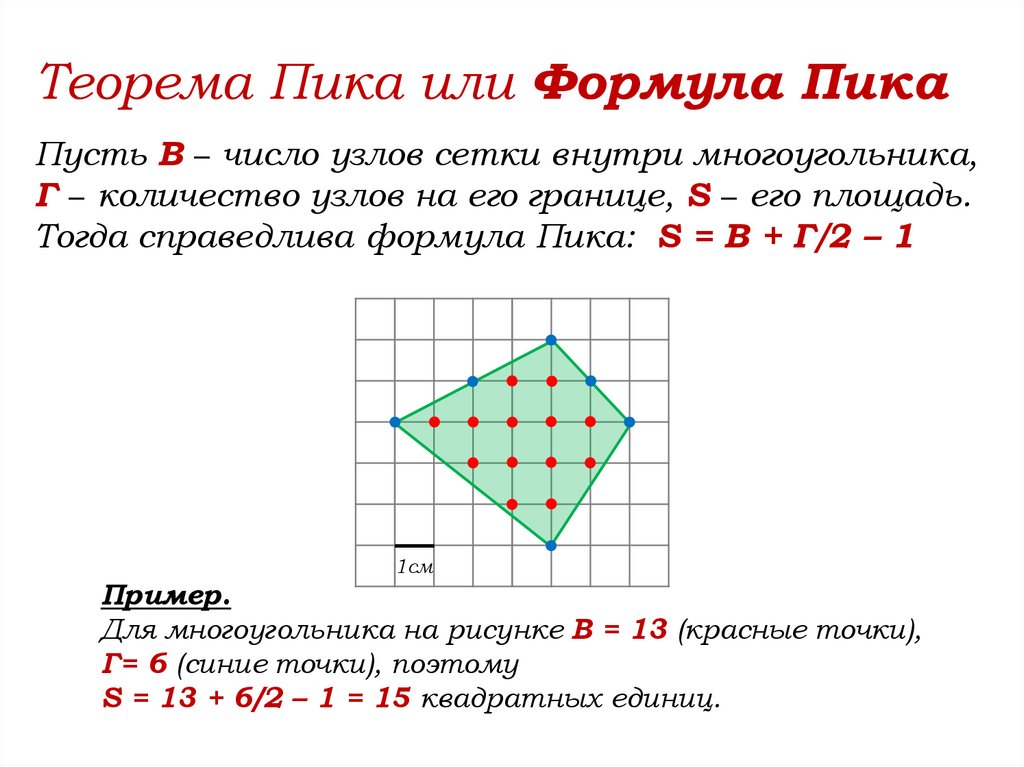
Теорема Пика или Формула ПикаПусть В − число узлов сетки внутри многоугольника,
Г − количество узлов на его границе, S − его площадь.
Тогда справедлива формула Пика: S = В + Г/2 – 1
1см
Пример.
Для многоугольника на рисунке В = 13 (красные точки),
Г= 6 (синие точки), поэтому
S = 13 + 6/2 – 1 = 15 квадратных единиц.
7. Найдём площадь многоугольника
Искать её можно по-разному.8. Способы, применяемые для вычисления площади данной фигуры
1способ: Подсчетколичества клеток (для
данной фигуры
приближенный).
2 способ: Попробовать
разрезать многоугольник
на достаточно простые
фигуры (рис.2), найти их
площади и сложить.
9.
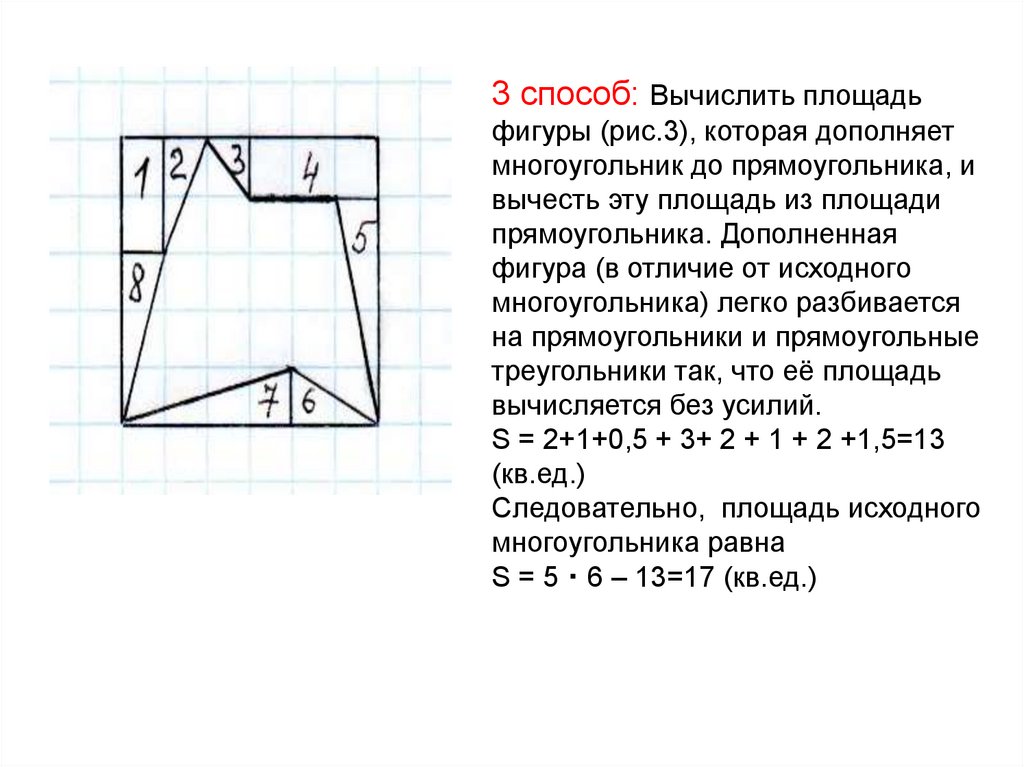
3 способ: Вычислить площадьфигуры (рис.3), которая дополняет
многоугольник до прямоугольника, и
вычесть эту площадь из площади
прямоугольника. Дополненная
фигура (в отличие от исходного
многоугольника) легко разбивается
на прямоугольники и прямоугольные
треугольники так, что её площадь
вычисляется без усилий.
S = 2+1+0,5 + 3+ 2 + 1 + 2 +1,5=13
(кв.ед.)
Следовательно, площадь исходного
многоугольника равна
S = 5・6 – 13=17 (кв.ед.)
10.
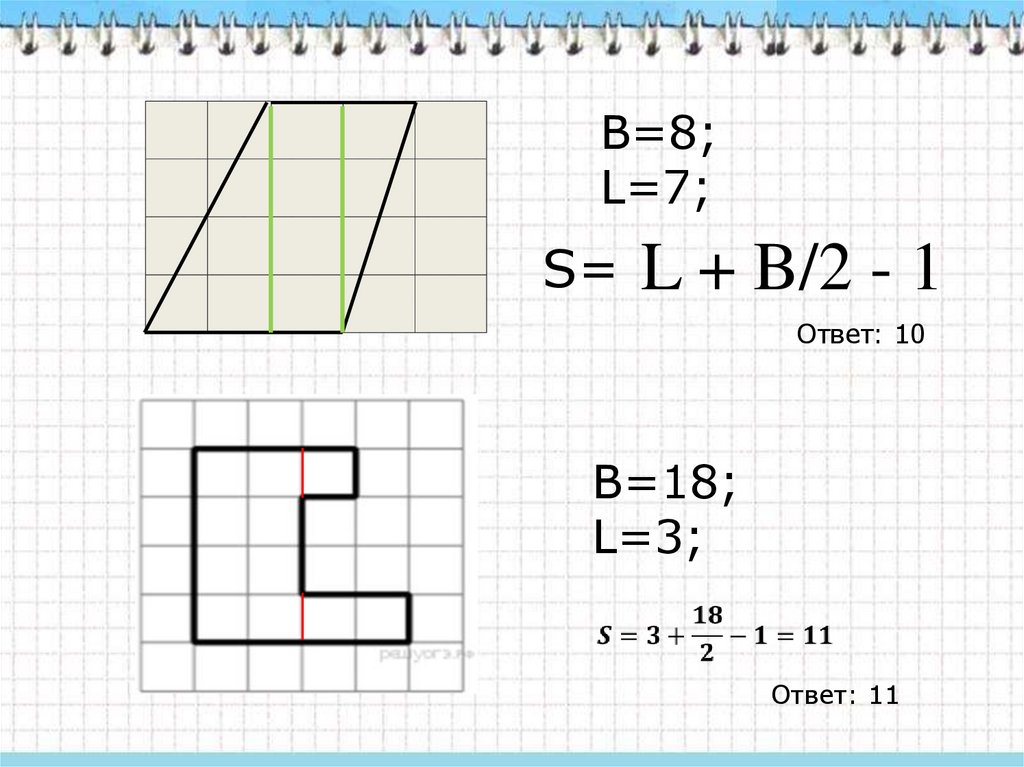
В=8;L=7;
S= L + B/2 - 1
Ответ: 10
В=18;
L=3;
Ответ: 11
11.
Теорема Пика или Формула ПикаПусть В − число узлов сетки внутри многоугольника,
Г − количество узлов на его границе, S − его площадь.
Тогда справедлива формула Пика: S = В + Г/2 – 1
1см
Пример.
Для многоугольника на рисунке В = 13 (красные точки),
Г= 6 (синие точки), поэтому
S = 13 + 6/2 – 1 = 15 квадратных единиц.
12.
Спасибо завнимание!







 mathematics
mathematics