Similar presentations:
Решение задач с помощью графов
1.
2.
Между девятью планетами солнечной системы установлено космическоесообщение. Рейсовые ракеты летают по следующим маршрутам: Земля –
Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий –
Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и
Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?
• Решение.
• Нарисуем схему: планетами будут
соответствовать точки, а соединяющим их
маршрутам – не пересекающиеся между
собой линии.
• Теперь видно, что долететь от Земли до
Марса нельзя.
• Ответ. Нельзя.
3.
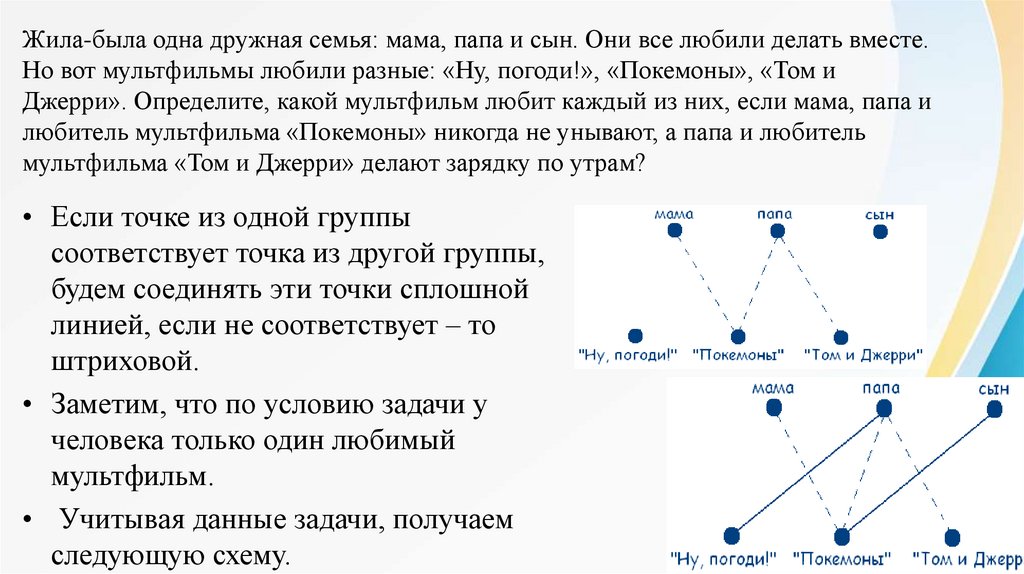
Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе.Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и
Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и
любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель
мультфильма «Том и Джерри» делают зарядку по утрам?
• Если точке из одной группы
соответствует точка из другой группы,
будем соединять эти точки сплошной
линией, если не соответствует – то
штриховой.
• Заметим, что по условию задачи у
человека только один любимый
мультфильм.
• Учитывая данные задачи, получаем
следующую схему.
4.
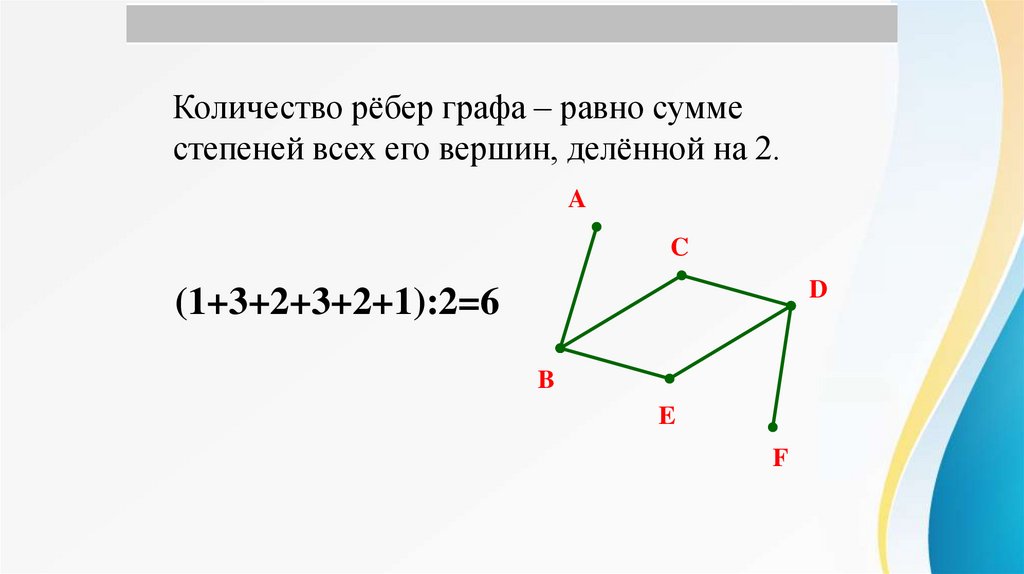
Количество рёбер графа – равно сумместепеней всех его вершин, делённой на 2.
A
C
D
(1+3+2+3+2+1):2=6
B
E
F
5.
Решение логических задач с помощью графов№1
В государстве 100 городов, а из каждого города выходит 4
дороги. Сколько всего дорог в государстве?
Решение:
Воспользуемся формулой: количество рёбер в графе равно
сумме степеней его вершин, делённой на 2.
(100 ∙ 4) : 2 = 200 .
6.
Решение логических задач с помощью графов№ 2
Может ли в государстве, в котором из каждого города
выходит 3 дороги, быть ровно 100 дорог?
Решение:
Воспользуемся формулой: количество рёбер в графе
равно сумме степеней его вершин, делённой на 2.
Нет, не может, так как
если X- число городов
x 3 : 2 100
x 200 : 3
7.
Решение логических задач с помощью графов№ 3
Аркадий, Борис, Владимир, Григорий и Дмитрий
при встрече обменялись рукопожатиями (каждый
пожал руку каждому по одному разу).
Сколько всего рукопожатий было сделано?
8.
Решение логических задач с помощью графовРешение:
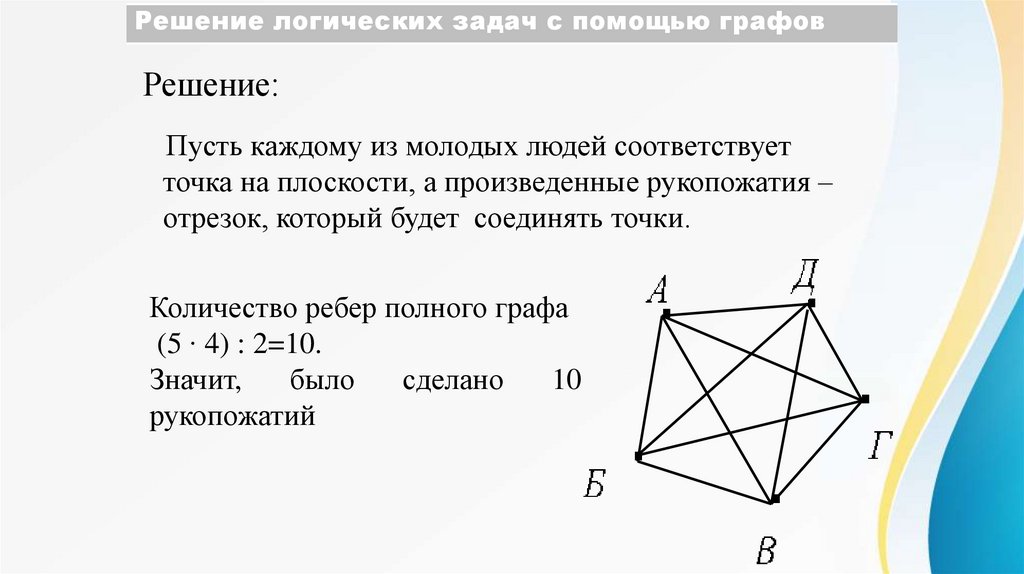
Пусть каждому из молодых людей соответствует
точка на плоскости, а произведенные рукопожатия –
отрезок, который будет соединять точки.
Количество ребер полного графа
(5 ∙ 4) : 2=10.
Значит,
было
сделано
10
рукопожатий
9.
Решение логических задач с помощью графов№ 4
• Алексей, Борис, Виталий и Геннадий – друзья.
• Один из них –врач, другой – журналист, третий – тренер
спортивной школы, четвертый – строитель.
• Журналист написал статьи об Алексее и Геннадие.
• Тренер и журналист вместе с Борисом ходили в поход.
• Алексей и Борис были на приеме у врача.
• У кого какая профессия?
10.
Решение логических задач с помощью графовАлексей, Борис, Виталий и Геннадий – друзья.
Один из них –врач, другой – журналист, третий – тренер спортивной школы,
четвертый – строитель.
Журналист написал статьи об Алексее и Геннадии.
Тренер и журналист вместе с Борисом ходили в поход.
Алексей и Борис были на приеме у врача.
У кого какая профессия?
Алексей
строитель
Борис
тренер
Виталий
журналист
Геннадий
врач
Изобразим все данные условия на рисунке с помощью графов
и ответ станет очевидным
11.
Домашнее задание• Задача
1.Семеро ученых, участвовавших в научной
конференции, обменялись рукопожатиями.
Сколько всего было сделано рукопожатий?
2. Н а рисунке - схема дорог, связывающих
города А, Б, В, Г, Д, Е, Ж.
По каждой дороге можно
двигаться только в одном
направлении, указанном
стрелкой. Сколько существует
различных путей из города А в город Ж?








 programming
programming