Графы как средства усиления межпредметных связей в курсе математики в средней школе

1.

ФГБОУ ВО «МЕЛИТОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Факультет естественных наук
Кафедра «Высшая математика, физика и методика преподавания физикоматематических дисциплин»
ТЕМА МАГИСТЕРСКОЙ РАБОТЫ
«Графы как средства усиления межпредметных
связей в курсе математики в средней школе »
Работу выполнила:
Студент(ка) Павлюк Дарья Андреевна 21 М ПМИ группы
Специальность
Инновационные технологии подготовки учителя в образовательной области
«Математика и информатика»
Руководитель проекта:
Халанчук Лариса Викторовна, к.ф.- м.н., доцент
Мелитополь, 2024

2.

Актуальность темы
Теория графов в настоящее время является интенсивно развивающимся разделом
математики. Это объясняется тем, что в виде графовых моделей описываются
различные объекты и ситуации, например планирование производства, составление
расписания транспорта с целью минимизации расходов или времени, проводится
финансовый анализ деятельности организации, что является важным для
нормального ежедневного функционирования общественной жизни.
Теория графов позволяет ученикам понять красоту математики, а это, в свою
очередь, несет воспитательный и мотивационный характер.
Обучающихся необходимо познакомить с теорией графов на факультативных
занятиях, научить оперировать терминами теории графов, использовать и применять
ее при решении задач.
Ведь графы способствуют развитию математического мышления. Применение
графов, не вызывая особых затруднений у школьников, может способствовать
наглядности обучения, при которой реальные объекты заменяются их знаковым
изображением.
Все вышесказанное определяет актуальность исследования.

3.

Объектом исследования данной выпускной квалификационной работы
является процесс обучения элементам теории графов на факультативных
занятиях в общеобразовательной школе.
Предметом исследования является методика преподавания основ теории графов
в общеобразовательной школе.
Цель исследования методическая разработка курса «Элементы теории графов в
средней школе» для обучающихся общеобразовательной школы.
Задачи исследования
Изучить элементы теории графов.
Разобрать решения различных видов задач.
Узнать о применении графов в науке и в различных сферах.
Изучить роль факультативных занятий как формы обучения математике.

4.

Гипотеза исследования проведение факультативных занятий по теории графов
способствует развитию у обучающихся математического мышления.
Методы исследования
1) Работа с различными источниками информации.
2) Описание, сбор, систематизация материала.
3) Наблюдение, анализ и сравнение.
4) Составление задач.
Научная новизна исследования
Практическая значимость исследования данной работы определяется тем, что
результаты могут быть использованы на информатике, математике, геометрии,
черчении и классных часах, а также для широкого круга читателей,
заинтересованных данной темой. Исследовательская работа имеет выраженную
практическую направленность, так как в работе представлены многочисленные
примеры применения графов во многих областях знаний, составлены свои
задачи. Данный материал можно использовать на факультативных занятиях по
математике.

5.

Одной из актуальных проблем последнего времени является проблема введения в
школьный курс математики теории графов. Эта теория находит свое применение
практически во всех областях знания, являясь одним из средств реализации
интеграционных связей математики, поэтому методически целесообразно не только
познакомить школьников с понятиями данной теории на уроках математики, но и
рассмотреть примеры ее использования в других науках: информатике, химии,
биологии, экономике.
Часто ли учителя математики и информатики
используют элементы теории графов на своих
уроках? Знают ли учащиеся о теории графов?
Понимают ли они, что графы — мощное средство
моделирования? Что же мешает учителю ввести в
факультативный курс теорию графов и показать, как
ее средствами можно легко решать нестандартные
задачи? Для ответа на эти вопросы был проведен
опрос среди учителей математики и учащихся.

6.

Исследования проходил на базе Мелитопольского государственного университета на кафедре высшей
математики, физики и методики преподавания физико-математических дисциплин. Был проведен опрос
среди учителей Запорожской области и Херсонской области и студентов 1 курсов. Целью исследования
было узнать их отношения к теории графов. Было опрошено 65 учителей математики и информатики и 50
студентов 1 курсов.
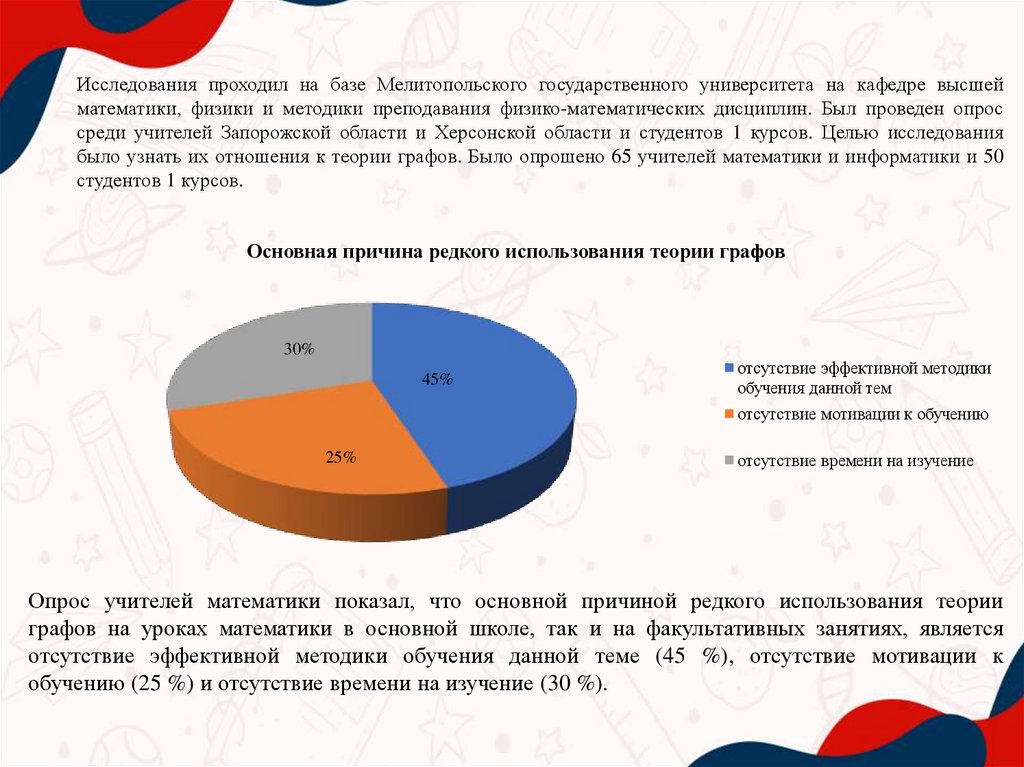
Основная причина редкого использования теории графов
30%
45%
отсутствие эффективной методики
обучения данной тем
отсутствие мотивации к обучению
25%
отсутствие времени на изучение
Опрос учителей математики показал, что основной причиной редкого использования теории
графов на уроках математики в основной школе, так и на факультативных занятиях, является
отсутствие эффективной методики обучения данной теме (45 %), отсутствие мотивации к
обучению (25 %) и отсутствие времени на изучение (30 %).

7.

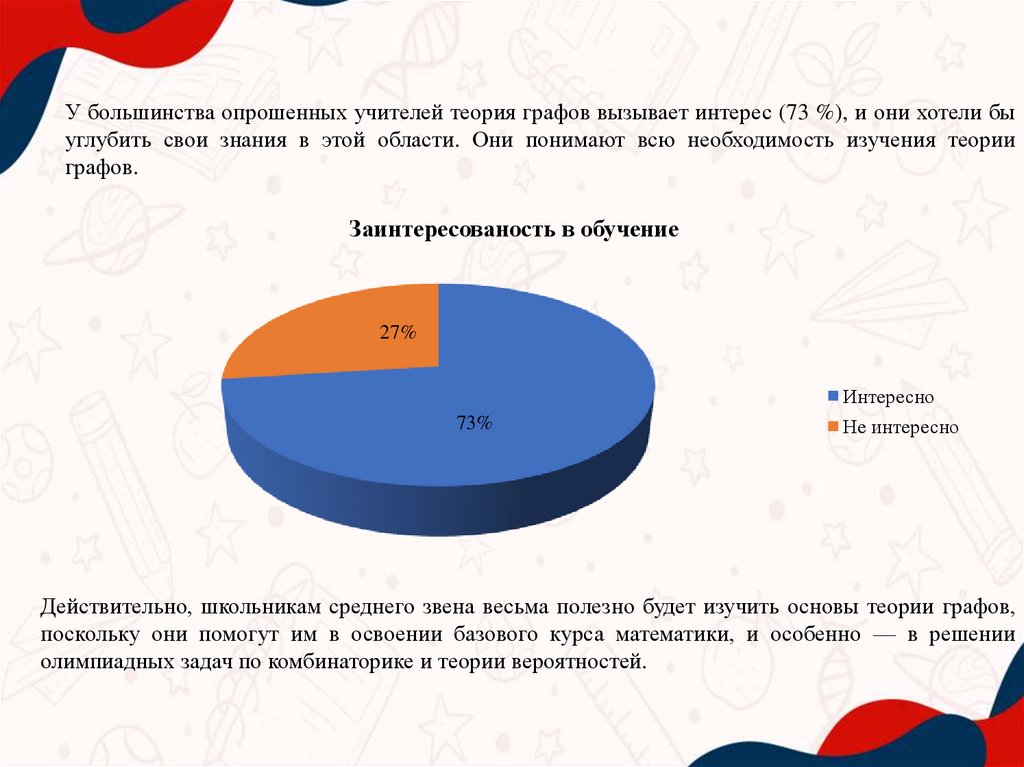
У большинства опрошенных учителей теория графов вызывает интерес (73 %), и они хотели бы
углубить свои знания в этой области. Они понимают всю необходимость изучения теории
графов.
Заинтересованость в обучение
27%
Интересно
73%
Не интересно
Действительно, школьникам среднего звена весьма полезно будет изучить основы теории графов,
поскольку они помогут им в освоении базового курса математики, и особенно — в решении
олимпиадных задач по комбинаторике и теории вероятностей.

8.

Использование межпредметных связей одна из наиболее сложных методических
задач учителя математики.
Она требует знаний содержания
программ и учебников по другим
предметам.
Реализация межпредметных связей в
практике
обучения
предполагает
сотрудничество учителя с учителями
химии, физики, посещения открытых
уроков, совместного планирования уроков
и т.д.

9.

Вопрос межпредметных связей в обучении является существенным и важным. Ведь, если
история «работает» на математику, математика – на информатику и на физику, физика –
на географию, география – на историю, то в голове человека возникает не мозаика
знаний, а полноценная мировоззренческая картина мира.

10.

Решая задачи, учащиеся совершают сложные познавательные и расчетные действия:
осознание сущности межпредметной задачи
понимание необходимости применения знаний из других предметов
отбор и актуализация нужных знаний из других предметов
их перенос в новую ситуацию
сопоставление знаний из смежных предметов
синтез знаний
установление совместимости понятий
единиц измерения
расчетных действий, их выполнение, получение результата, обобщение в выводах,
закрепление понятий.

11.

Использование
графов
имеет
естественную тенденцию к развитию.
Применение графов помогает развитию
абстрактного и творческого мышления,
способствует умению наглядно мыслить.
«Учитель
должен
так
организовать учебный процесс,
чтобы заинтересовать ученика,
привить ему интерес к предмету».
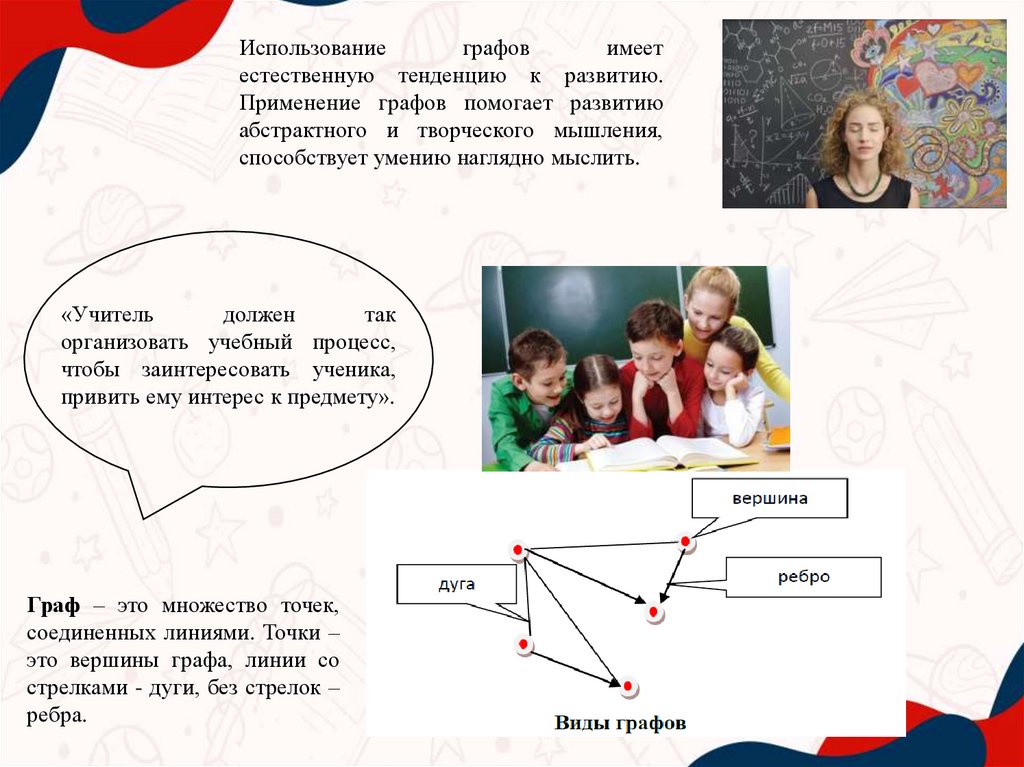
Граф – это множество точек,
соединенных линиями. Точки –
это вершины графа, линии со
стрелками - дуги, без стрелок –
ребра.

12.

13.

Связность графа
Граф называется связным, если любая пара его вершин связана. Связными
компонентами графа называются подграфы данного графа, вершины
которых связаны.
Деревья
Дерево — это связный граф без циклов. Деревья особенно часто возникают на практике при
изображении различных иерархий. Например, популярны генеалогические деревья.
Граф без цикла называется лесом. Вершины степени 1 в дереве называются
листьями. Деревья - очень удобный инструмент представления информации самого
разного вида. Деревья отличаются от простых графов тем, что при обходе дерева
невозможны циклы. Это делает графы очень удобной формой организации данных
для различных алгоритмов. Таким образом, понятия дерева активно используется в
информатике и программировании.

14.

Таблица сравнения типов графов
Тип графа
Определение
Ориентированный граф
Граф, в котором каждое ребро имеет направление
Неориентированный граф
Граф, в котором ребра не имеют направления
Взвешенный граф
Граф, в котором каждому ребру присвоено числовое
значение (вес)
Невзвешенный граф
Граф, в котором ребра не имеют числовых значений
(весов)
Связный граф
Граф, в котором есть путь между любыми двумя
вершинами
Несвязный граф
Граф, в котором есть вершины, между которыми нет
пути

15.

Язык графов отличается простотой и понятностью, он
очень естественный. Мы часто используем графы, но
не догадываемся или не задумываемся над этим. Графы
могут выступать отличным средством для знакомства
школьников с построением моделей. Еще до того, как
ученики познакомятся с понятием модели, их можно
учить строить простейшие модели с помощью графов.
Графовые задачи помогают улучшить логическое
мышление. Представляя объекты в наглядной
форме, графы помогают лучше запоминать и
усваивать новые знания, а так же устанавливать
связь между ними.
Применение
графов
в
решении
задач
способствует
повышению
внимания,
т.к.
мыслительная
деятельность
сопровождается
соответствующей моторной деятельностью, а
объекты,
которыми
мы
оперируем,
воспринимаются зрительно

16.

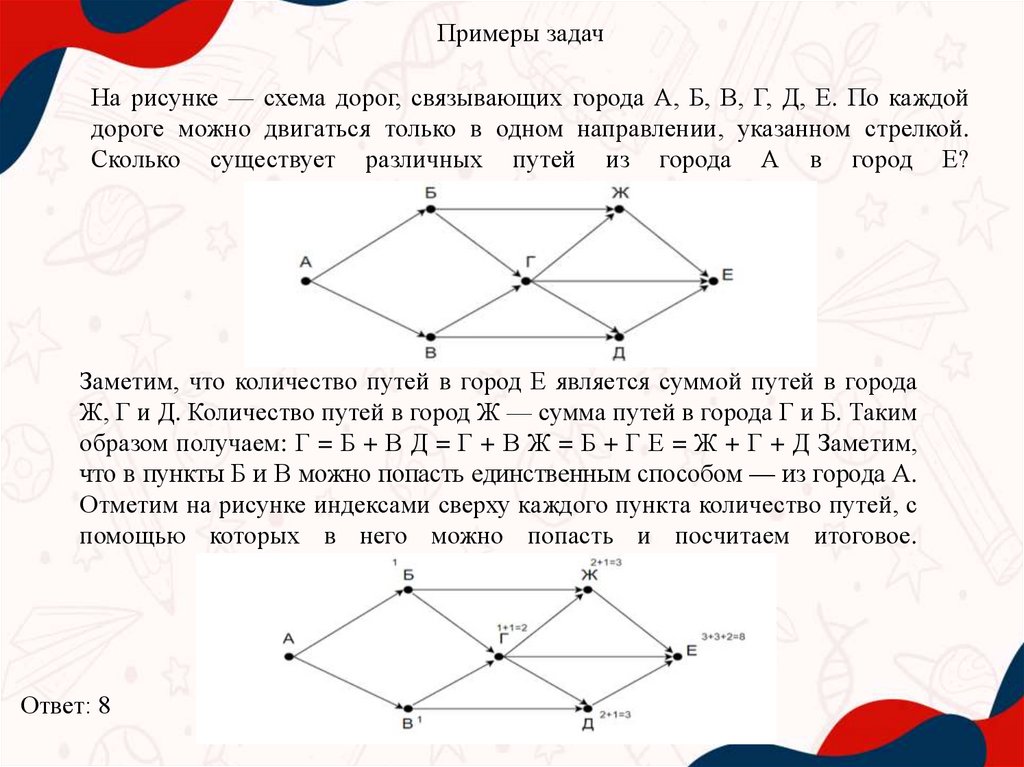
Примеры задач
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой
дороге можно двигаться только в одном направлении, указанном стрелкой.
Сколько существует различных путей из города А в город Е?
Заметим, что количество путей в город Е является суммой путей в города
Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким
образом получаем: Г = Б + В Д = Г + В Ж = Б + Г Е = Ж + Г + Д Заметим,
что в пункты Б и В можно попасть единственным способом — из города А.
Отметим на рисунке индексами сверху каждого пункта количество путей, с
помощью которых в него можно попасть и посчитаем итоговое.
Ответ: 8

17.

Геральт спешит выручить Цири из плена Кагыра. В таблице указана протяжённость
дорог между пунктами, через которые он может пройти. Укажите длину самого
короткого участка кратчайшего пути от Геральта до Цири (от точки И до точки М).
Передвигаться
можно
только
по
дорогам,
указанным
в
таблице:
Найдём все варианты маршрутов из И в М и выберем самый короткий. Из пункта И
можно попасть в пункты А, Б, Г, М. Из пункта Г можно попасть в пункты И, М. Из
пункта В можно попасть в пункты А, Б. Из пункта Б можно попасть в пункты В, И, М.
И—А—В—Б—М: длина маршрута 7 км. И—Б—М: длина маршрута 4 км. И—Г—М:
длина маршрута 7 км. И—М: длина маршрута 8 км. Самый короткий путь: И—Б—М.
Длина маршрута 4 км. Самый короткий участок этого пути равен 1 км.
Ответ: 1

18.

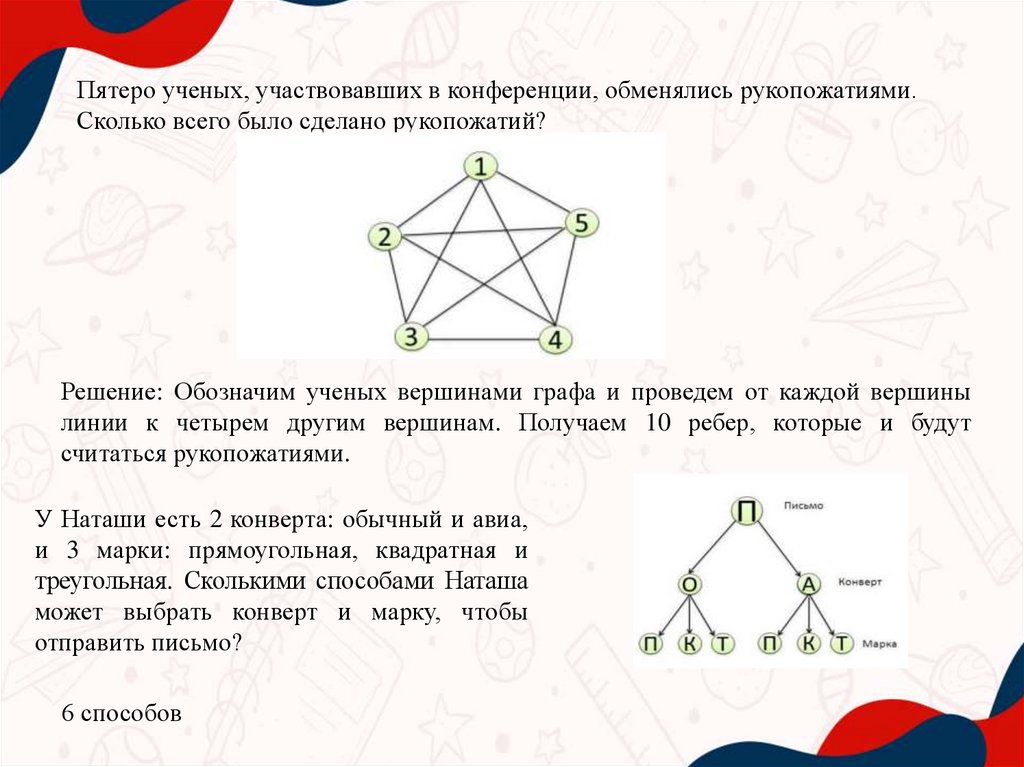
Пятеро ученых, участвовавших в конференции, обменялись рукопожатиями.
Сколько всего было сделано рукопожатий?
Решение: Обозначим ученых вершинами графа и проведем от каждой вершины
линии к четырем другим вершинам. Получаем 10 ребер, которые и будут
считаться рукопожатиями.
У Наташи есть 2 конверта: обычный и авиа,
и 3 марки: прямоугольная, квадратная и
треугольная. Сколькими способами Наташа
может выбрать конверт и марку, чтобы
отправить письмо?
6 способов

19.

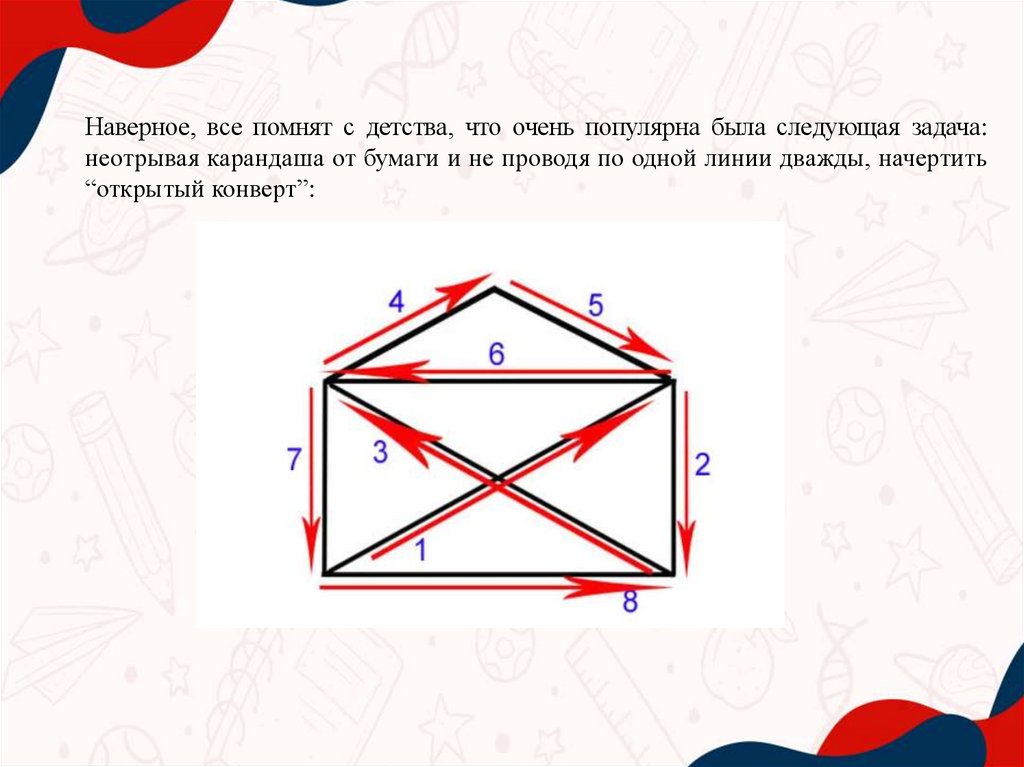
Наверное, все помнят с детства, что очень популярна была следующая задача:
неотрывая карандаша от бумаги и не проводя по одной линии дважды, начертить
“открытый конверт”:

20.

На уроках не всегда есть возможность строить графы.
Как правило из за отсутствия достаточного количества
времени. Однако эта деятельность остается полезной и
может быть реализована как дома, так и на внеклассных
занятиях, факультативном курсе.
Для того чтобы у обучающихся сформировалось
положительное представление о теории графов,
отдельные вопросы из этого раздела, стоит вводить на
факультативных занятиях, начиная с 5-го класса. Задачи
по теории графов следует рассматривать и на некоторых
уроках математики, как задачи, развивающие логическое
мышление. Вводить их нужно постепенно, начиная с
элементарных заданий. При первом знакомстве с такими
задачами учителю не следует объявлять ученикам, что их
нужно решать, используя теорию графов.

21.

Мне неизвестно как
решать такие задачи
Новый неизвестный термин может психологически испугать обучающихся: «мне неизвестно
как решать такие задачи», хотя зачастую решение может быть быстрым и простым. Когда
учащиеся будут уверены в своих силах, следует сообщить, что эти задания выделяют в особый
раздел математики — теорию графов. Детальное рассмотрение темы стоит вынести в
содержание факультативного курса. Первостепенной задачей является раскрытие возможности
графов как средств обучения учащихся решению задач. Затем следует разработать содержание
факультативных занятий, отражающих основные положения теории графов. Сведения о них
нужно углублять по мере изучения темы. Таким образом, к выпускным экзаменам у
обучающихся должно сформироваться представление об изучении теории графов в школе.

22.

Включение данного факультативного курса в
систему предпрофильной подготовки дополнит
базовую программу, не нарушая её целостности, и
будет способствовать развитию математического
мышления. Важным аспектом курса является
использование полученных знаний и умений для
решения практических задач в повседневной
жизни.
Цель факультативного курса: углубление и
расширение
математических
знаний
обучающихся, развитие их математической
культуры, интереса к изучению математики,
математического
мышления,
внимания,
наблюдательности
и
их
творческих
способностей.

23.

Настоящий факультативный курс направлен на решение следующих задач:
формирование у обучающихся системы знаний и умений по теме «Элементы теории
графов в средней школе»;
развитие умения видеть и использовать приобретённые знания и умения в
практической деятельности и повседневной жизни;
формирование умений и навыков исследовательской деятельности;
развитие умения анализировать, синтезировать, обобщать;
воспитание усидчивости, настойчивости в достижении цели;
развитие навыков личностного характера, таких как коммуникативность, умение
работать в команде, взаимопомощь, развитие лидерских и организаторских качеств,
умение отстаивать свою точку зрения;
развитие математического мышления;
формирование понимания значимости математики среди других наук.

24.

Немаловажным аспектом эффективности учебно-воспитательного процесса является подбор
разнообразных форм учебной деятельности, таких как урок-практикум, урок-беседа, урок
обобщающей задачи, работа в группах, защита творческих работ.
В результате изучения курса обучающиеся должны знать:
основные понятия и утверждения теории графов;
определение эйлерова и гамильтонового графов и их элементов;
определение лабиринта и правила решения задач на лабиринты
определение графов с цветными рёбрами и их свойства.

25.

В результате изучения данного факультативного курса развиваются следующие
общеучебные и профильные умения и. навыки:
- учебно-организаторские;
- учебно-интеллектуальные;
- учебно-коммуникативные;
- учебно-информационные.
Факультативный курс «Элементы теории графов в средней школе» рассчитан на 16
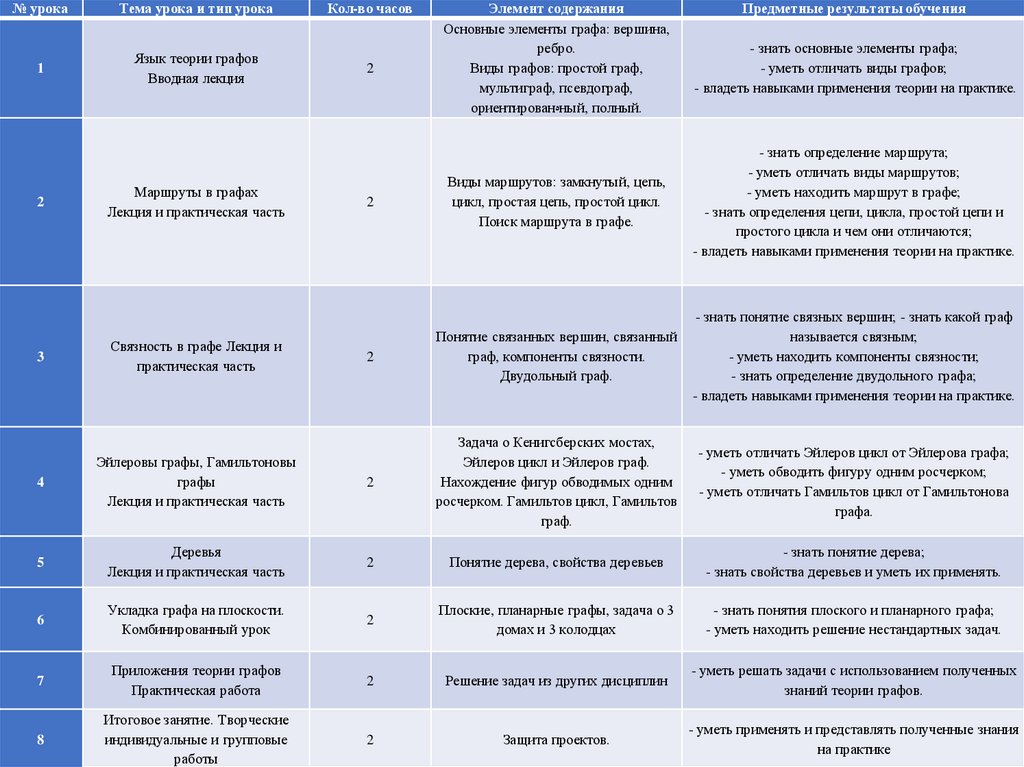
часов и включает в себя 8 тем (таблица 2.1).
Результатом усвоения материала факультативного курса является написание и защита
обучающимися творческих работ к итоговому занятию по одной из предложенных
тем. Знания, полученные после прохождения факультативного курса «Элементы
теории графов в средней школе» возможно, практически реализовать в средней школе
при решении олимпиадных задач, в области математики и информатики. Все задачи
для практической части занятий факультативного курса и темы докладов вынесены в
Приложение 1 к выпускной квалификационной работе.

26.

№ урока
Тема урока и тип урока
1
Язык теории графов
Вводная лекция
Кол-во часов
2
Элемент содержания
Основные элементы графа: вершина,
ребро.
Виды графов: простой граф,
мультиграф, псевдограф,
ориентирован‫ہ‬ный, полный.
Предметные результаты обучения
- знать основные элементы графа;
- уметь отличать виды графов;
- владеть навыками применения теории на практике.
Виды маршрутов: замкнутый, цепь,
цикл, простая цепь, простой цикл.
Поиск маршрута в графе.
- знать определение маршрута;
- уметь отличать виды маршрутов;
- уметь находить маршрут в графе;
- знать определения цепи, цикла, простой цепи и
простого цикла и чем они отличаются;
- владеть навыками применения теории на практике.
2
Понятие связанных вершин, связанный
граф, компоненты связности.
Двудольный граф.
- знать понятие связных вершин; - знать какой граф
называется связным;
- уметь находить компоненты связности;
- знать определение двудольного графа;
- владеть навыками применения теории на практике.
4
Эйлеровы графы, Гамильтоновы
графы
Лекция и практическая часть
2
Задача о Кенигсберских мостах,
Эйлеров цикл и Эйлеров граф.
Нахождение фигур обводимых одним
росчерком. Гамильтов цикл, Гамильтов
граф.
- уметь отличать Эйлеров цикл от Эйлерова графа;
- уметь обводить фигуру одним росчерком;
- уметь отличать Гамильтов цикл от Гамильтонова
графа.
5
Деревья
Лекция и практическая часть
2
Понятие дерева, свойства деревьев
- знать понятие дерева;
- знать свойства деревьев и уметь их применять.
6
Укладка графа на плоскости.
Комбинированный урок
2
Плоские, планарные графы, задача о 3
домах и 3 колодцах
- знать понятия плоского и планарного графа;
- уметь находить решение нестандартных задач.
7
Приложения теории графов
Практическая работа
2
Решение задач из других дисциплин
- уметь решать задачи с использованием полученных
знаний теории графов.
8
Итоговое занятие. Творческие
индивидуальные и групповые
работы
2
Защита проектов.
- уметь применять и представлять полученные знания
на практике
2
3
Маршруты в графах
Лекция и практическая часть
Связность в графе Лекция и
практическая часть
2

27.

СПАСИБО ЗА ВНИМАНИЕ !