Применение теории графов к решению логических задач

1. Секция: ПРОГРАММИРОВАНИЕ ПРИМЕНЕНЕИЕ ТЕОРИИ ГРАФОВ К РЕШЕНИЕЮ ЛОГИЧЕСКИХ ЗАДАЧ

Городская проектная неделя
«Обучение, вдохновение, творчество»
Секция: ПРОГРАММИРОВАНИЕ
ПРИМЕНЕНЕИЕ ТЕОРИИ ГРАФОВ
К РЕШЕНИЕЮ ЛОГИЧЕСКИХ
ЗАДАЧ
Моисеенко Александр, Васильев Алексей
МОУ «Средняя общеобразовательная школа №9»
г. Канаш, 11 класс
Канаш
Научный руководитель:
Кузьмин Вячеслав Алексеевич,
учитель информатики
СОШ № 9 г. Канаш

2.

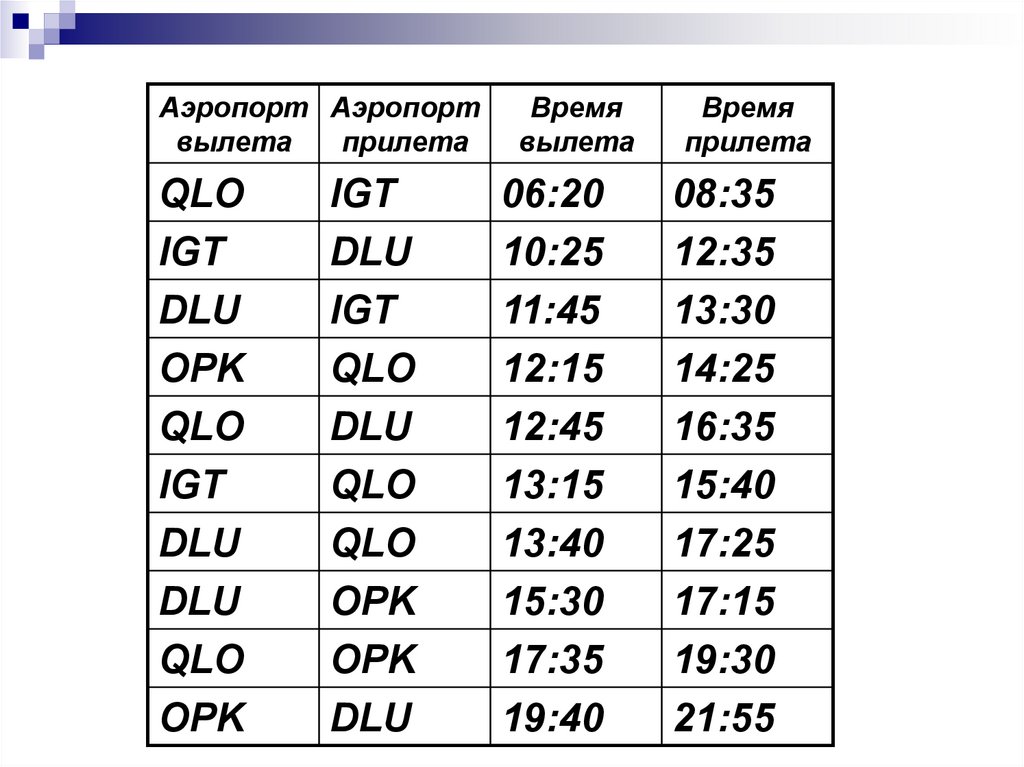
Аэропорт Аэропорт
вылета
прилета
QLO
IGT
DLU
OPK
QLO
IGT
DLU
DLU
QLO
OPK
IGT
DLU
IGT
QLO
DLU
QLO
QLO
OPK
OPK
DLU
Время
вылета
06:20
10:25
11:45
12:15
12:45
13:15
13:40
15:30
17:35
19:40
Время
прилета
08:35
12:35
13:30
14:25
16:35
15:40
17:25
17:15
19:30
21:55

3. Результаты опроса учащихся 11 класса

Знакомо ли вам понятие "граф"?
Количество учащихся
35
30
27
29
25
20
Ряд1
15
10
5
2
0
Математическое
понятие
Титул
Математическое
понятие и как
титул

4.

ЦЕЛЬ И ЗАДАЧИ ИССЛЕДОВАНИЯ
Цель исследования: применить графовый
аппарат для решения логических задач.
Гипотеза: На наш взгляд, решение многих
логических задач будет менее трудоемким,
если мы будем использовать для этого теорию
графов.
Задачи исследования:
рассмотреть решение задач при помощи
графов;
научиться переводить задачи на язык графов;
сравнить традиционные методы решения
задач с методами теории графов.

5. Основные ПОНЯТИЯ ТЕОРИИ ГРАФОВ

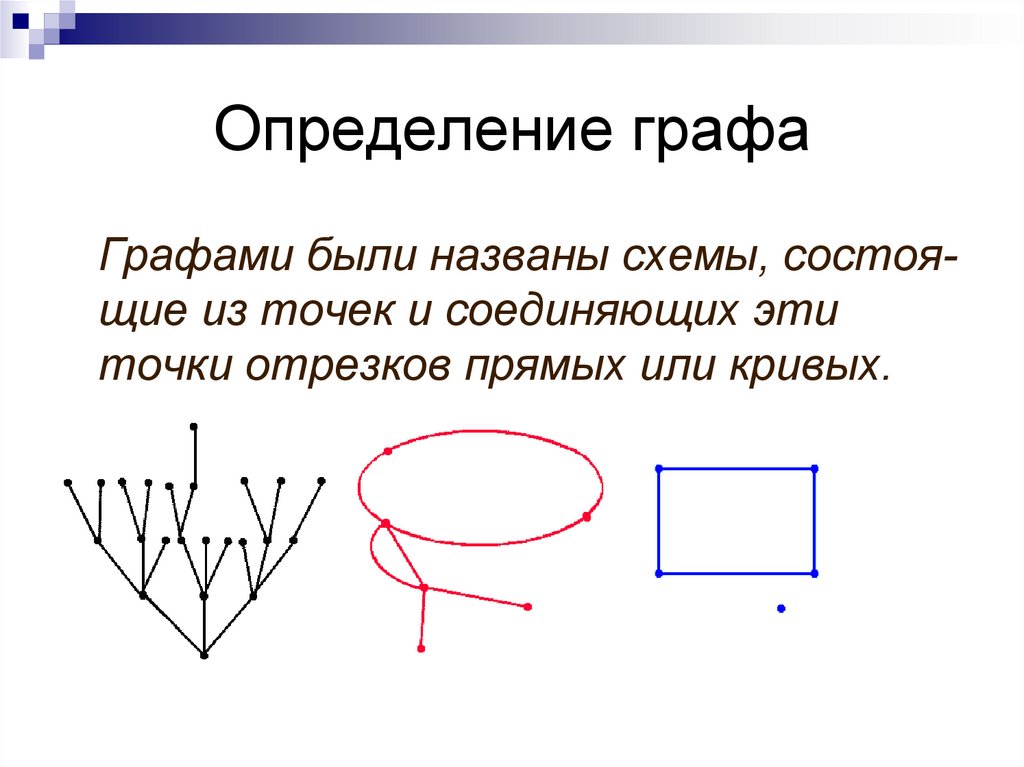
6. Определение графа

Графами были названы схемы, состоящие из точек и соединяющих эти
точки отрезков прямых или кривых.

7. Кенигсбергские мосты

Самая известная задача,связанная с теорией графов – о
кенигсбергских мостах.
К XVIII веку через реку, на которой стоял город Кенигсберг
(ныне Калининград), было построено 7 мостов, которые
связывали с берегами и друг с другом два острова,
расположенные в пределах города (см.рисунок)

8. Решение Леонарда Эйлера

Прохождение по всем мостам при
условии, что нужно на каждом
побывать один раз и вернуться в
точку начала путешествия, на
языке теории графов выглядит
как задача изображения «одним
росчерком» графа,
представленного на рисунке. Но,
поскольку граф на этом рисунке
имеет четыре нечетные
вершины, то, согласно
закономерности 7. такой граф
начертить «одним росчерком»
невозможно. Значит, и пройти по
кенигсбергским мостам, соблюдая
заданные условия, нельзя.

9. Следующим типом задач являются задачи нахождения наилучших вариантов развозки товаров по магазинам, материалов по стройкам,

т.е. нахождения оптимального
маршрута.
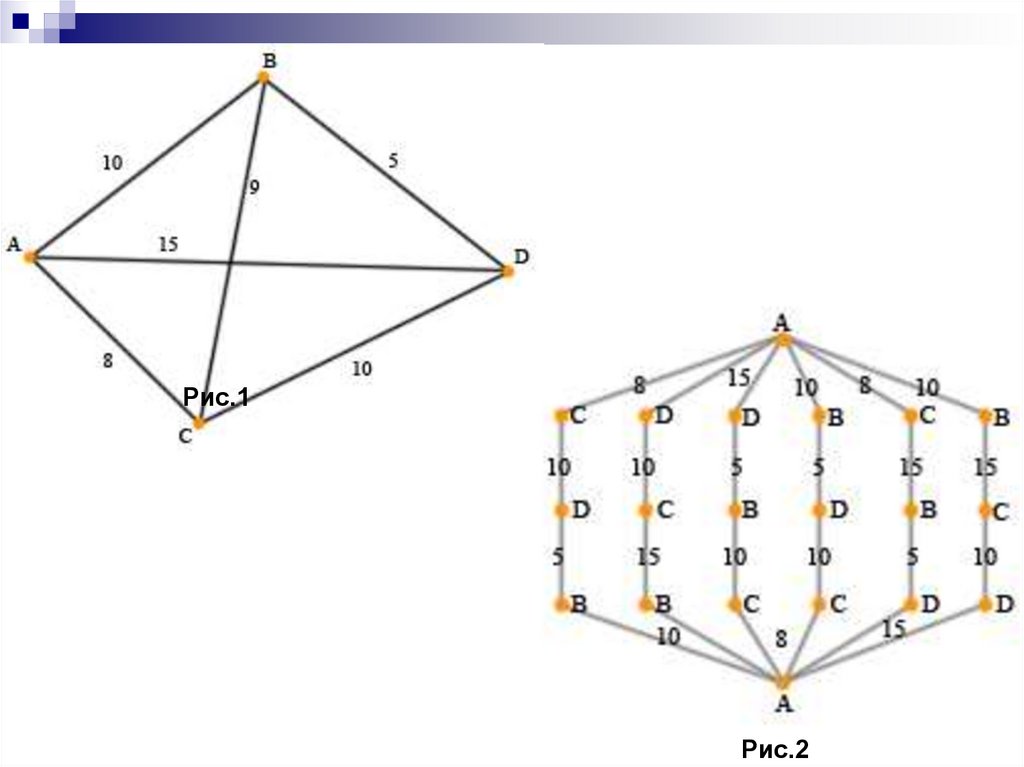
Например, имеется 4 города,
расстояния между которыми
известны. Необходимо найти
кратчайший маршрут между этими
городами.

10.

Рис.1
Рис.2

11. Применение элементов теории графов к решению задач в заданиях единого государственного экзамена по информатике

Задание А10 из демоверсии ЕГЭ по информатике.
Между четырьмя крупными аэропортами,
обозначенными кодами DLU, IGT, OPK и
QLO, ежедневно выполняются авиарейсы.
Приведён фрагмент расписания перелётов
между этими аэропортами:

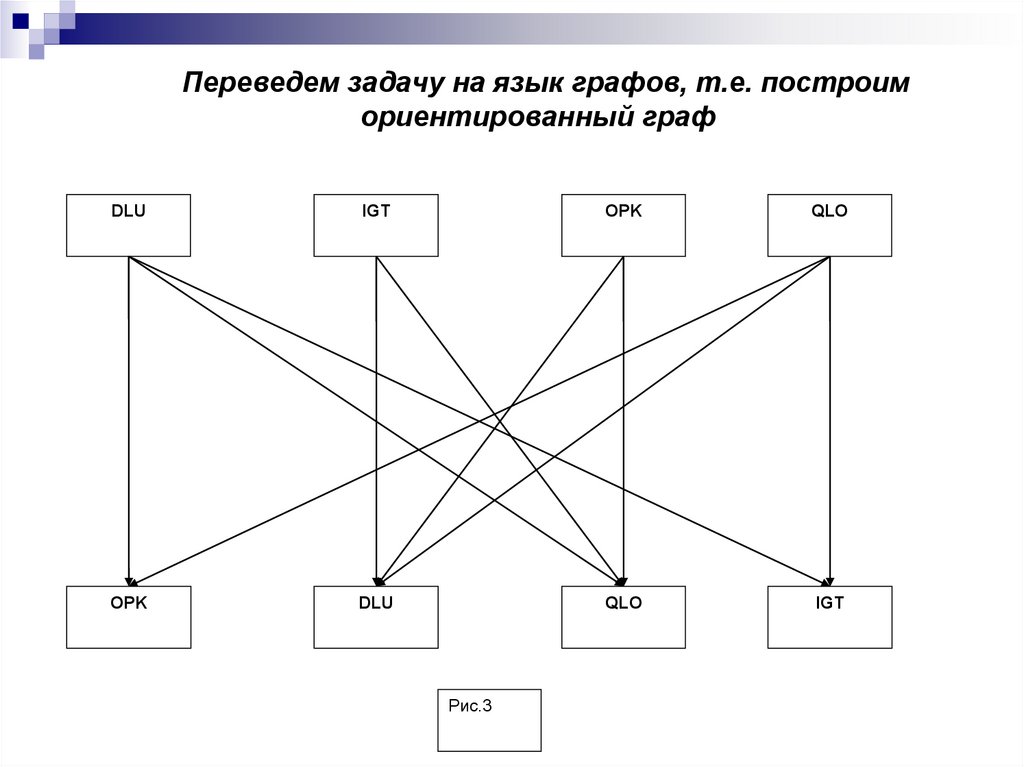
12. 13. Переведем задачу на язык графов, т.е. построим ориентированный граф

DLU
IGT
OPK
QLO
OPK
DLU
QLO
IGT
Рис.3

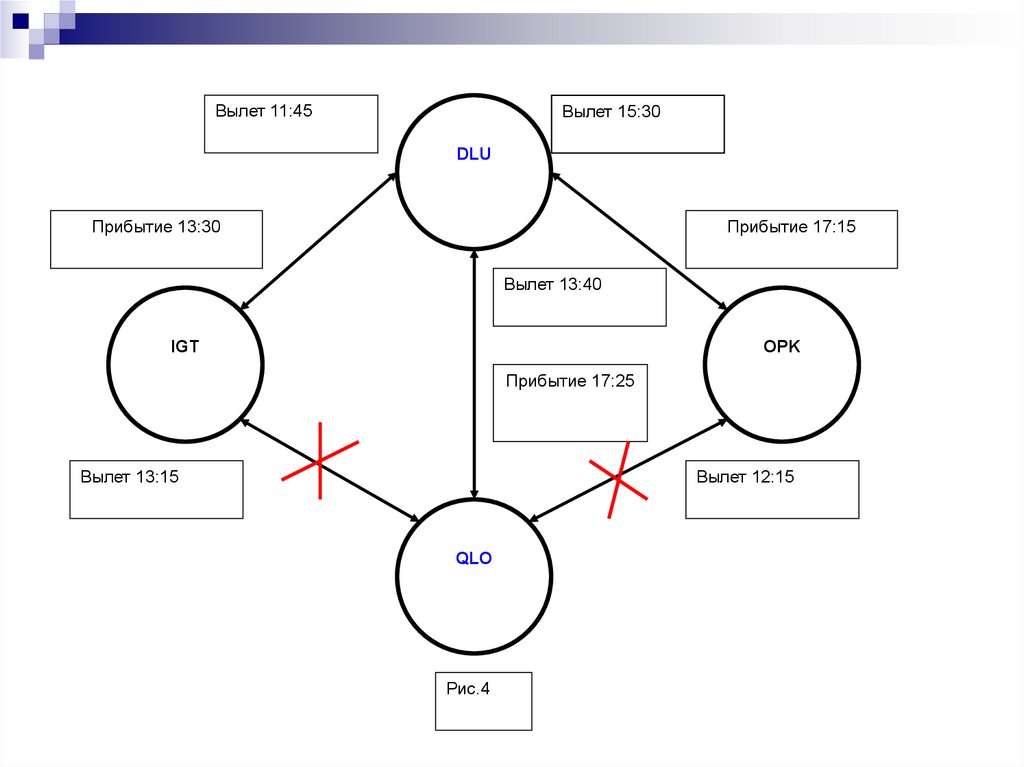
14.

Вылет 11:45
Вылет 15:30
DLU
Прибытие 13:30
Прибытие 17:15
Вылет 13:40
IGT
OPK
Прибытие 17:25
Вылет 13:15
Вылет 12:15
QLO
Рис.4

15. Заключение

При решении логических задач обычно бывает достаточно
трудно держать в памяти многочисленные факты, данные в
условии, устанавливать связь между ними, высказывать
гипотезы, делать частные выводы и пользоваться ими.
На помощь приходят графы. Выделяя из словесных
рассуждений главное — объекты и отношения между ними,
графы представляют изучаемые факты в наглядной форме и
помогают проследить все логические возможности изучаемой
ситуации. Благодаря своей обозримости, позволяют тут же, в
ходе решения задачи, классифицировать логические
возможности, отбрасывать неподходящие случаи, не доводя до
полного перебора всех случаев. Что подтверждает нашу
гипотезу.

English Русский Rules