Similar presentations:
Цифровая обработка сигналов. Случайные процессы, белый шум
1.
Цифровая обработка сигналовЛекция 4
Тема: Случайные процессы, белый шум
2.
СигналыВ предыдущих частях мы узнали, что сигнал - это физический процесс, параметры
которого изменяются в соответствии с передаваемым сообщением.
бывают – случайные и детерминированные.
Сигналы
Случайным сигналом называют функцию времени, значения которой заранее
неизвестны и могут быть предсказаны лишь с некоторой
вероятностью. К основным характеристикам случайных сигналов относятся:
закон распределения (относительное время пребывания значения сигнала в
определенном интервале),
спектральное распределение мощности.
Случайные сигналы делятся на два класса:
1) шумы - беспорядочные колебания, состоящие из набора разных частот и
амплитуд,
2) сигналы, несущие информацию, для обработки которых требуется прибегать к
вероятностным методам.
3.
Сигналы• Случайные
сигналы
характеризуются
плотностью
распределения
вероятностей.
• Плотность вероятности это один из способов задания распределения случайных
величин. Плотность вероятности - неотрицательная функция при любых
значениях дискретного сигнала.
• Для аналоговых случайных сигналов интеграл от функции сигнала во всем
диапазоне значений стремится к единице.
• Для дискретных случайных величин не существует функции плотности
распределения вероятностей, т.к. дискретная случайная величина не является
непрерывной функцией. Однако, математический аппарат позволяет вычислять
приближенные значения функции.
Простые примеры дискретных случайных величин:
количество выпавших орлов и количество выпавших решек при броске монеты
счетное число N раз,
число попаданий в мишень при ограниченном числе выстрелов.
погрешности измерений приборов
4.
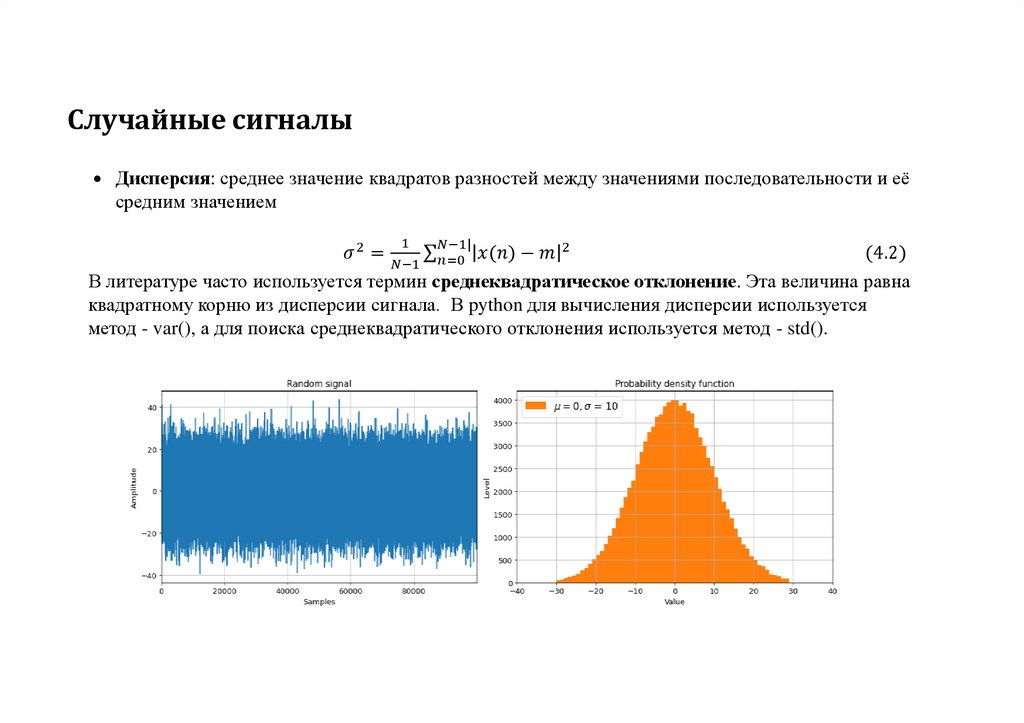
Случайные сигналыПлотность вероятности случайного сигнала позволяет определить математические
моменты разного порядка:
Математическое ожидание: среднее значение последовательности случайных
величин








 physics
physics








