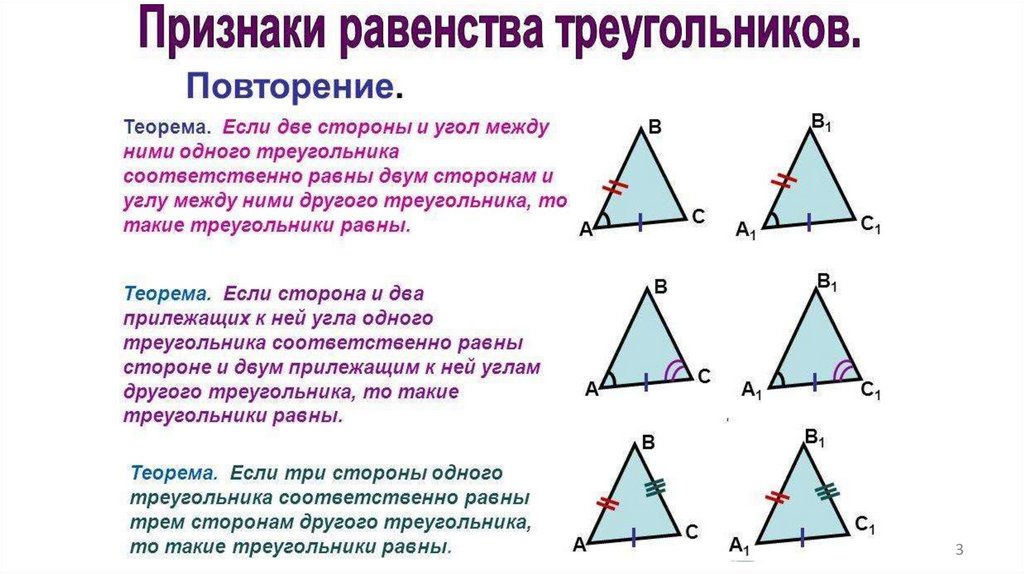
Параллелограмм. Диагонали параллелограмма

1.

Параллелограмм
1

2.

2

3.

3

4.

4

5.

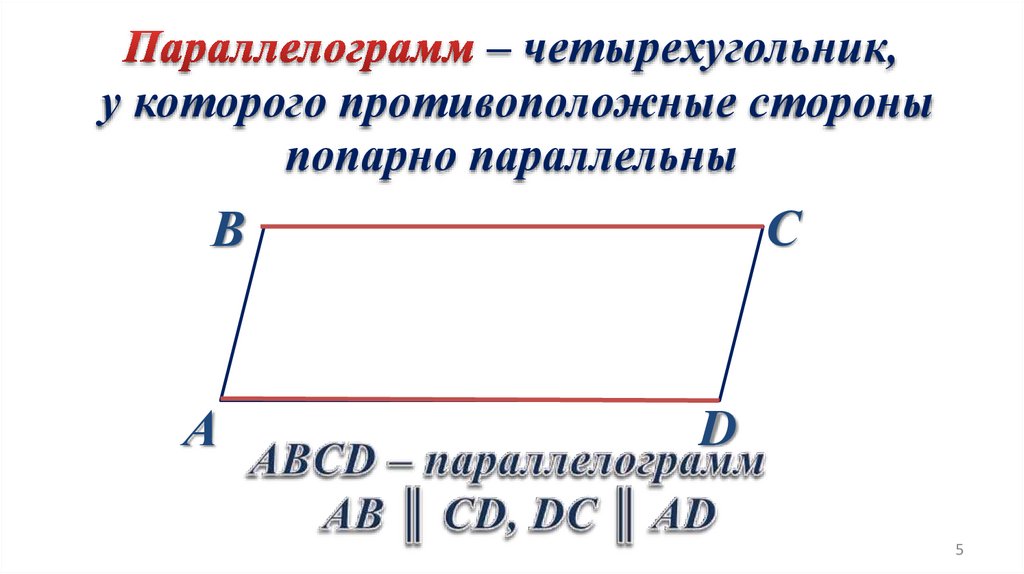
– четырехугольник,
у которого противоположные стороны
попарно параллельны
С
В
А
D
5

6.

С
В
1
А
D
В параллелограмме противоположные стороны
равны и противоположные углы равны.
6

7.

В
2
С
О
А
D
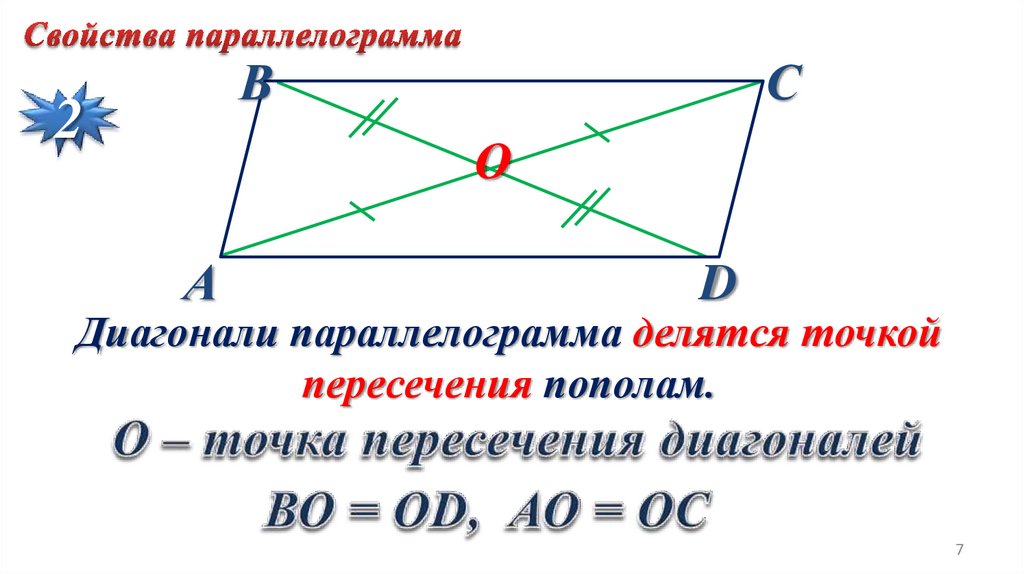
Диагонали параллелограмма делятся точкой
пересечения пополам.
7

8.

1
Признаки параллелограмма
Если в четырехугольнике две стороны равны и параллельны,
то этот четырехугольник параллелограмм
В
С
А
D
Дано:
Доказать:
АВСD – четырехугольник,
АВ = CD, АВ ∥ CD
АВСD – параллелограмм
8

9.

1
В
1
А
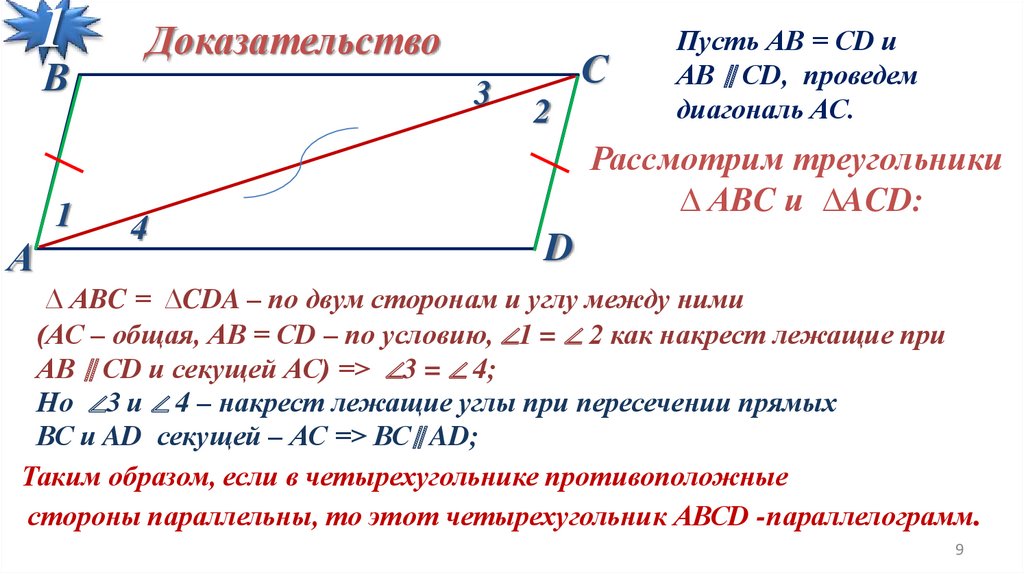
Доказательство
3
4
С
2
Пусть АВ = СD и
АВ ∥ СD, проведем
диагональ АС.
Рассмотрим треугольники
∆ АBC и ∆ACD:
D
∆ АBC = ∆CDA – по двум сторонам и углу между ними
(АС – общая, АВ = СD – по условию, ∠1 = ∠ 2 как накрест лежащие при
АВ ∥ СD и секущей АС) => ∠3 = ∠ 4;
Но ∠3 и ∠ 4 – накрест лежащие углы при пересечении прямых
ВС и AD секущей – АС => ВС∥ AD;
Таким образом, если в четырехугольнике противоположные
стороны параллельны, то этот четырехугольник АВСD -параллелограмм.
9

10.

2
Признаки параллелограмма
Если в четырехугольнике противоположные стороны попарно
равны, то этот четырехугольник - параллелограмм.
В
С
А
D
Дано:
Доказать:
АВСD – четырехугольник,
АВ = CD, ВС = АD
АВСD – параллелограмм
10

11.

2
Доказательство
В
1
А
3
2
САВСD- четырехугольник,
D
Рассмотрим треугольники
∆ АBC и ∆ACD:
4
АВ = CD, ВС = АD.
Проведем диагональ АС.
∆ АBC = ∆ CDA – по трем сторонам
(АС – общая, АВ = СD, ВС = АD – по условию);
Из равенства треугольников:∠1 = ∠ 2, а это накрест лежащие при секущей
АС => АВ ∥ СD;
Так как АВ ∥ СD и АВ = СD, то четырехугольник АВСD – параллелограмм
(если в четырехугольнике две стороны равны и параллельны, то этот
четырехугольник параллелограмм).
11

12.

3
Признаки параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой
пересечения делятся пополам, то этот четырехугольник
параллелограмм.
В
С
О
D
Дано:
Доказать:
АВСD – четырехугольник,
ВО = ОD, АО = ОС
АВСD – параллелограмм
А
12

13.

3
Доказательство
В
С
2
4
D
АВСD –
четырехугольник,
ВО = ОD, АО = ОС.
3
О
Проведем диагонали АС и BD.
1
А
Рассмотрим треугольники
∆ АОB и ∆CОD:
∆ АОB = ∆CОD – по первому признаку равенства треугольников
(ВО = ОD, АО = ОС – по условию, ∠ АОB = ∠ CОD – как вертикальные);
Из равенства треугольников АВ=СD и ∠1 = ∠2 ,
а это накрест лежащие углы =>АВ ∥ CD;
Так как в четырехугольнике АВСD стороны АВ = CD и АВ ∥ CD,
то АВСD – параллелограмм (если в четырехугольнике две стороны
равны и параллельны, то этот четырехугольник параллелограмм).
13

14.

1
Задача
Дано:
Доказать:
В
А
АВСD – четырехугольник,
∠BАC = ∠ACD, ∠CAD =∠BCA
АВСD – параллелограмм.
С
Доказательство
D
14

15.

Рассмотрим треугольники ∆ АBC
и ∆ACD:
В
С
1. ∠BАC = ∠ACD, ∠CAD =∠BCA – по
условию, АС – общая;
следовательно ∆ АBC = ∆CDА– по А
стороне и двум прилежащим углам;
поэтому ВС = AD.
D
2.Так как ∠BАC = ∠ACD – накрест лежащие углы при
параллельных прямых ВС, AD и секущей - АС, то ВС ∥ AD.
3.Так как ВС = AD и ВС ∥ AD, то по 1-му признаку
параллелограмма АВСD – параллелограмм, что и требовалось
доказать.
15

16.

Особое свойство ромба
Диагонали ромба взаимно перпендикулярны
В
и делят его углы пополам.
12
BD перпендикулярно AC, ∠1 = ∠ 2
А
О
D
С
Доказательство:
Рассмотрим ∆АВС: АВ=ВС (по определению ромба)
=> ∆АВС – равнобедренный.
Точка О – точка пересечения диагоналей
параллелограмма, значит, т. О середина АС =>
ВО – медиана, биссектриса и высота ∆АВС =>
∠1 = ∠ 2 и BО ꓕ AC (значит, BD ꓕ AC).

17.

Квадрат
это ромб, у которого
все углы прямые
90°
90°
это параллелограмм, у
которого все стороны равны
и все углы равны
90°
90°
это прямоугольник, у
которого все стороны
равны

18.

В
А
О
D
С
Так как квадрат это параллелограмм,
прямоугольник и ромб, то для него
справедливы все свойства этих фигур:
1. В квадрате противоположные стороны
равны и противоположные углы равны;
2. Диагонали квадрата делятся точкой
пересечения пополам;
3. Диагонали квадрата равны;
4. Диагонали квадрата взаимно
перпендикулярны и делят углы пополам.

19.

Задача 1.
В выпуклом
четырехугольнике АВСD
В
AB=BC и AD=CD, ∠В=60°,
∠D=110°.
С
D
А
Найдите ∠А.

20.

Решение задачи 1.
1. Проведем диагональ АС
2. ∆ ADC - равнобедренный => ∠DCA=
∠CAD=(180° - ∠D) : 2 = (180° - 110°) : 2 = 35°
С
60°
D
110°
35°
60°
А
3. ∆ ABC - равнобедренный =>
В ∠DCA= ∠DAС= (180° - ∠B) : 2 =
= (180° - 60°) : 2 = 60°
4. ∠DAB= ∠CAB + ∠DAC = 35° + 60° = 95°
Ответ: 95°

21.

Задача 2.
В
А
65°
Диагональ BD параллелограмма ABCD
образует с его сторонами углы, равные
65° и 50°. Найдите меньший угол
параллелограмма.
С
50°
D

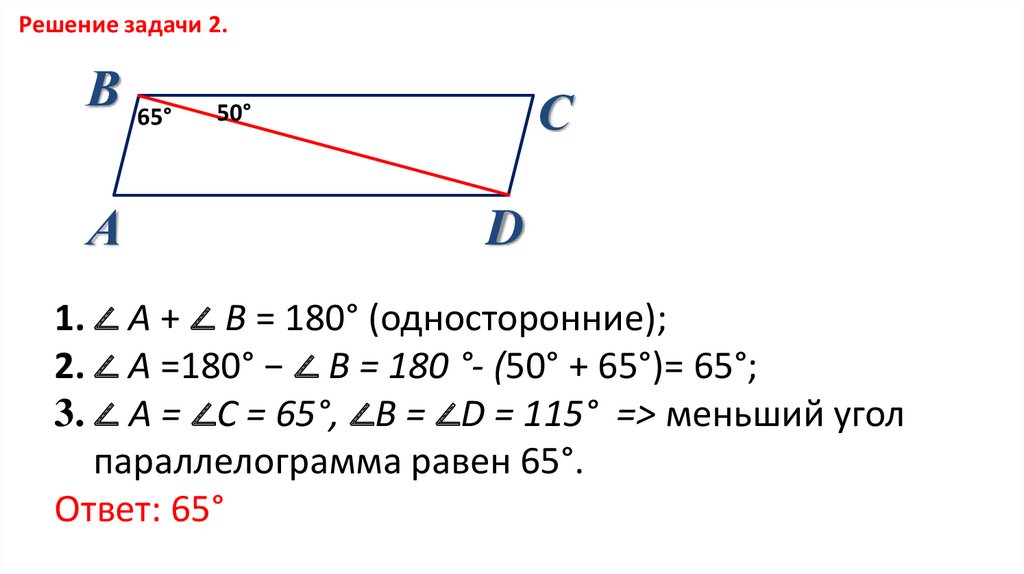
22.

Решение задачи 2.
В
А
65°
С
50°
D
1. ∠ А + ∠ В = 180° (односторонние);
2. ∠ А =180° − ∠ В = 180 °- (50° + 65°)= 65°;
3. ∠ А = ∠С = 65°, ∠В = ∠D = 115° => меньший угол
параллелограмма равен 65°.
Ответ: 65°

23.

Задача 3.
Разность углов, прилежащих к одной
стороне параллелограмма, равна 40°.
Найдите больший угол параллелограмма.
В
А
С
D

24.

Решение задачи 3.
В
С
х
А
D
1. Пусть ∠ А = х, тогда ∠ В = х + 40°
2. ∠ А + ∠ В = 180° (односторонние углы) =>
х + (х + 40°) = 180 ° => 2х = 140° => х = 70°,
то есть ∠ А= ∠С = 70°, а ∠ В= ∠ D = 110°.
Ответ: 110°

25.

Задача 4.
А
D
Найдите меньший угол равнобедренной
трапеции, если два ее угла
относятся как 1:2.
В
С

26.

Решение задачи 4.
D
А
х
2х
В
С
1. Пусть ∠ D = х, тогда ∠ А = 2х;
2. ∠ А + ∠ D = 180° (односторонние углы) =>
х + 2х = 180 ° => 3х = 180° => х = 60°,
то есть ∠ А= ∠B = 120°, а ∠ C= ∠D = 60°
(в равнобедренной трапеции углы при основании равны).
Ответ: 60°

27.

Задача 5.
Сторона ромба равна 34 см, а острый
угол равен 60° . Высота ромба,
опущенная из вершины тупого угла,
делит сторону на два отрезка.
Каковы длины этих отрезков?
В
А
С
D

28.

Решение задачи 5.
В
Н
А
D
С
1. Пусть ∠ А - тупой, тогда ∠В – острый и
∠В = 60°, АН – высота ромба;
2. ∆ АВН - прямоугольный и ∠В = 60° =>
∠ВАН = 30° => ВН = ⅟2 АВ (катет, лежащий
напротив угла в 30°, равен половине гипотенузы) =>
ВН = 17 см, НС = ВС – ВН = 34 – 17= 17 см.
Ответ: 17 см и 17 см

29.

Задача 6.
Биссектриса угла A прямоугольника
ABCD пересекает сторону DC в точке K.
Найдите периметр параллелограмма,
если DK = 6, CK = 8.
А
В
D
С
K

30.

Решение задачи 6.
1. ∠КАВ = ∠DAK, так как АК – биссектриса;
2. DC=AВ=6 + 8 = 14 см;
3. ∠ВАК= ∠АКD как накрест лежащие углы при AB ║ DC и секущей АК;
4. ∆ ADK – равнобедренный по признаку, так как ∠АКD = ∠DAK =>
DA=DK=6 см, но DA=BC => ВС = 6 см;
5. Р = AD + DC + CB + AB = 6 + 14 + 6 + 14 = 40 см
14
А
В
6
6
D
6
K
8
С
Ответ: 40 см