Similar presentations:
Признаки параллелограмма
1.
Уж реже солнышко блистало,Короче становился день,
Лесов таинственная сень
С печальным шумом обнажалась.
Ложился на поля туман,
Гусей крикливых караван
Тянулся к югу: приближалась
Довольно скучная пора;
(А.С. Пушкин)
Скажите о каком времени года идет речь? Почему
вы так решили?
В стихотворении А.С. Пушкина перечисляются
признаки осени или указывается о признаках
осени.
• Как вы считаете, а признаки бывают только у
времени года? Или другие объекты или явления
тоже имеют признаки?
2.
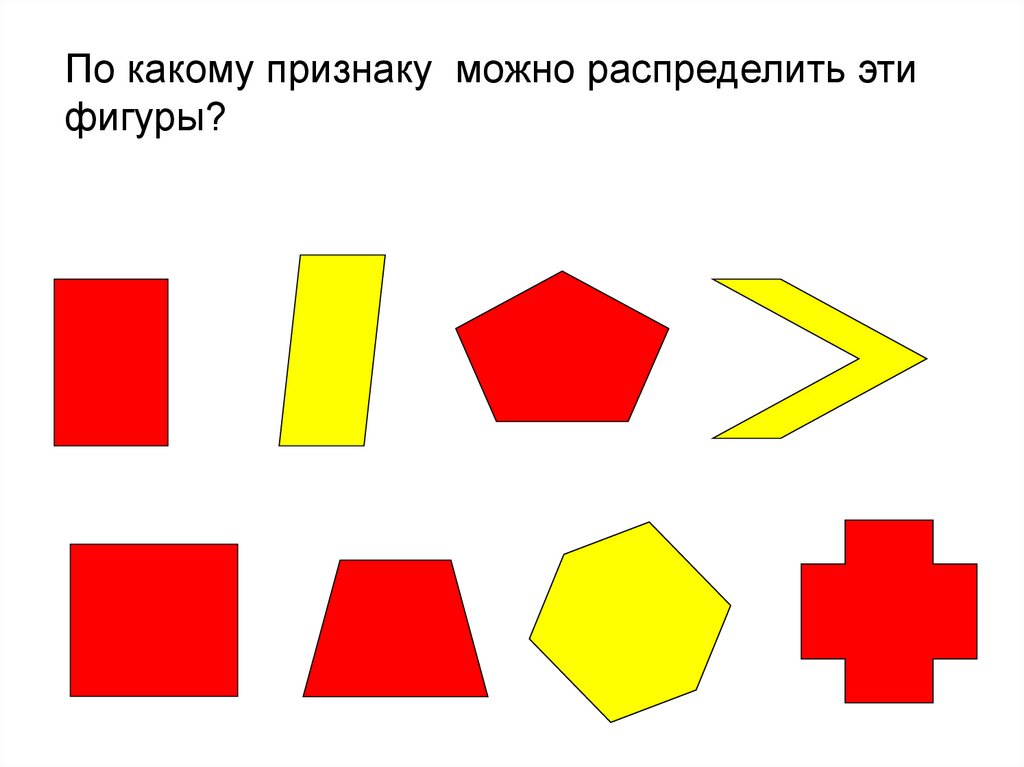
По какому признаку можно распределить этифигуры?
3.
Признакипараллелограмма
4.
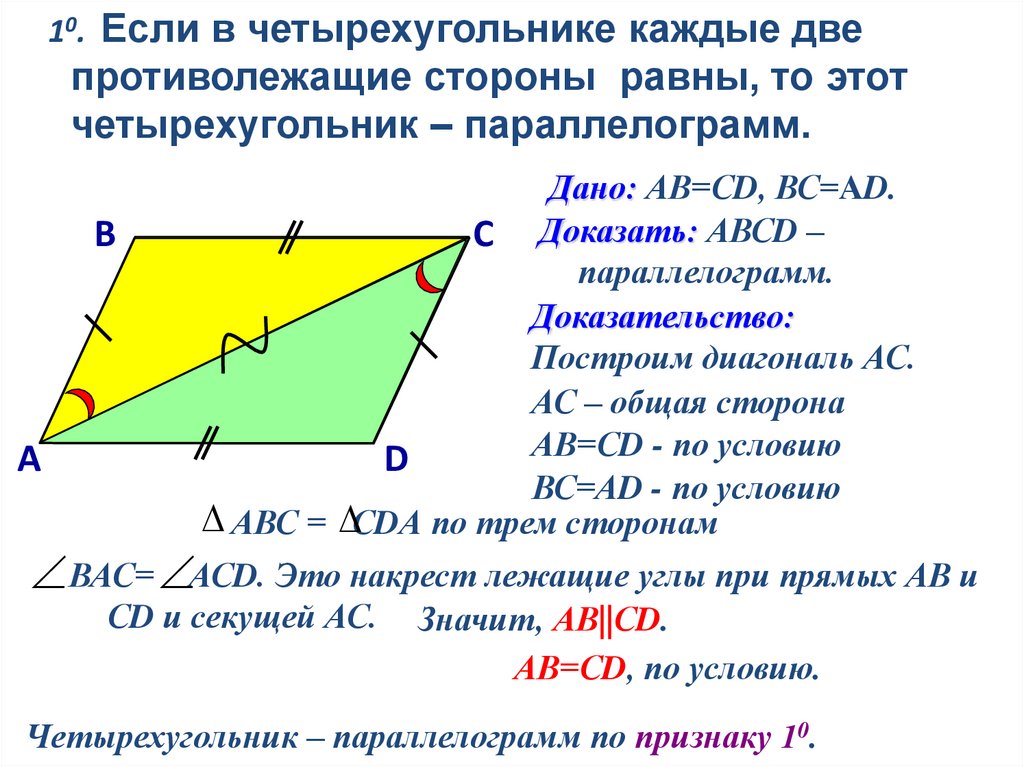
10. Если в четырехугольнике каждые двепротиволежащие стороны равны, то этот
четырехугольник – параллелограмм.
В
А
Дано: АВ=СD, ВС=АD.
С Доказать: АВСD –
параллелограмм.
Доказательство:
Построим диагональ АС.
АС – общая сторона
АВ=СD - по условию
D
ВС=АD - по условию
АВС = СDА по трем сторонам
ВАС= АСD. Это накрест лежащие углы при прямых АВ и
СD и секущей АС.
Значит, АВ||СD.
АВ=СD, по условию.
Четырехугольник – параллелограмм по признаку 10.
5.
20. Если в четырехугольнике двепротиволежащие стороны равны и параллельны,
то этот четырехугольник – параллелограмм.
Дано: АBCD - четырёхуг.
В
С АВ=СD, АВ || CD.
Доказать: АВСD –
параллелограмм.
Доказательство:
Построим диагональ АС.
АС – общая сторона
А
D
АВ=СD - по условию
ВАС= АСD как накрест лежащие углы
АВС = СDА по 2 сторонам и углу между ними.
Следовательно,
ВСА= САD. Это накрест лежащие углы при прямых ВС и
АD и секущей АС.Значит, ВС||AD.
Четырехугольник – параллелограмм по определению.
6.
30. Если в четырехугольнике диагонали точкойпересечения делятся пополам, то этот
четырехугольник – параллелограмм.
Дано:
В
А
АС ВD О, О середина АС и ВD.
Доказать: АВСD –
параллелограмм.
О
Доказательство:
АО=ОС - по условию
ВО=ОD- по условию
АОВ= СОD, как
D
вертикальные
АОВ = СОD по первому признаку
С
Отсюда, АВ=СD
ВАО= ОСD. Это накрест лежащие углы при прямых АВ и
СD и секущей АС. Значит, АВ||СD.
Четырехугольник – параллелограмм по признаку 10.
7.
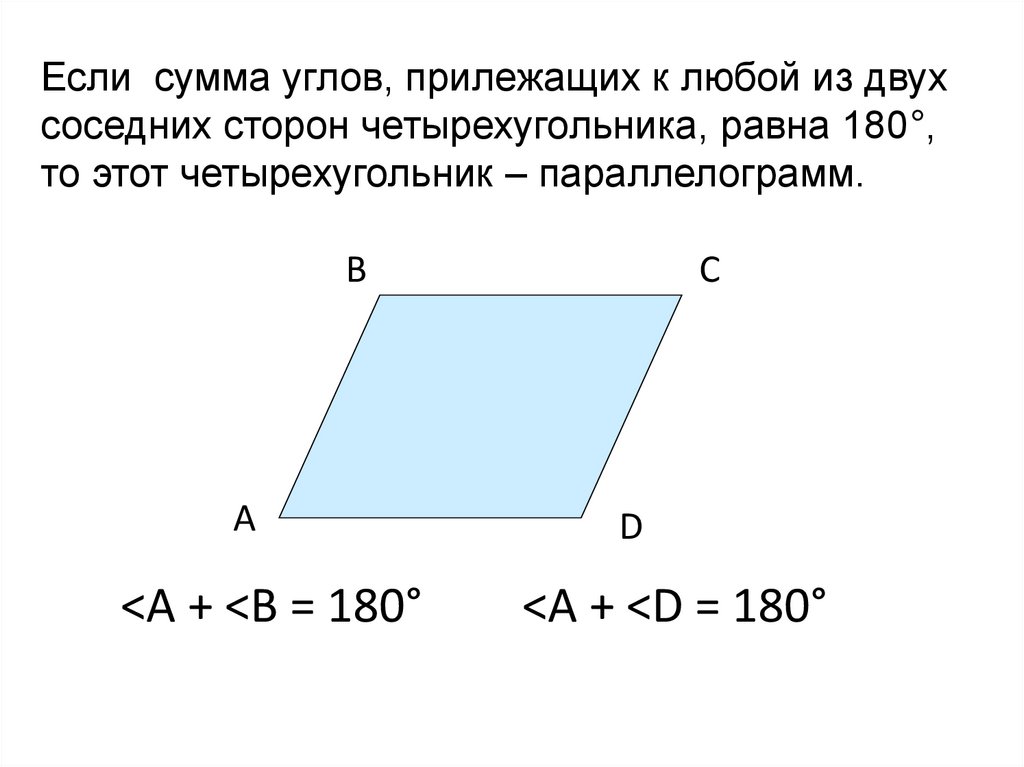
Если сумма углов, прилежащих к любой из двухсоседних сторон четырехугольника, равна 180°,
то этот четырехугольник – параллелограмм.
В
А
<A + <B = 180°
С
D
<A + <D = 180°




 mathematics
mathematics








