Грани. Вершины. Ребра

1.

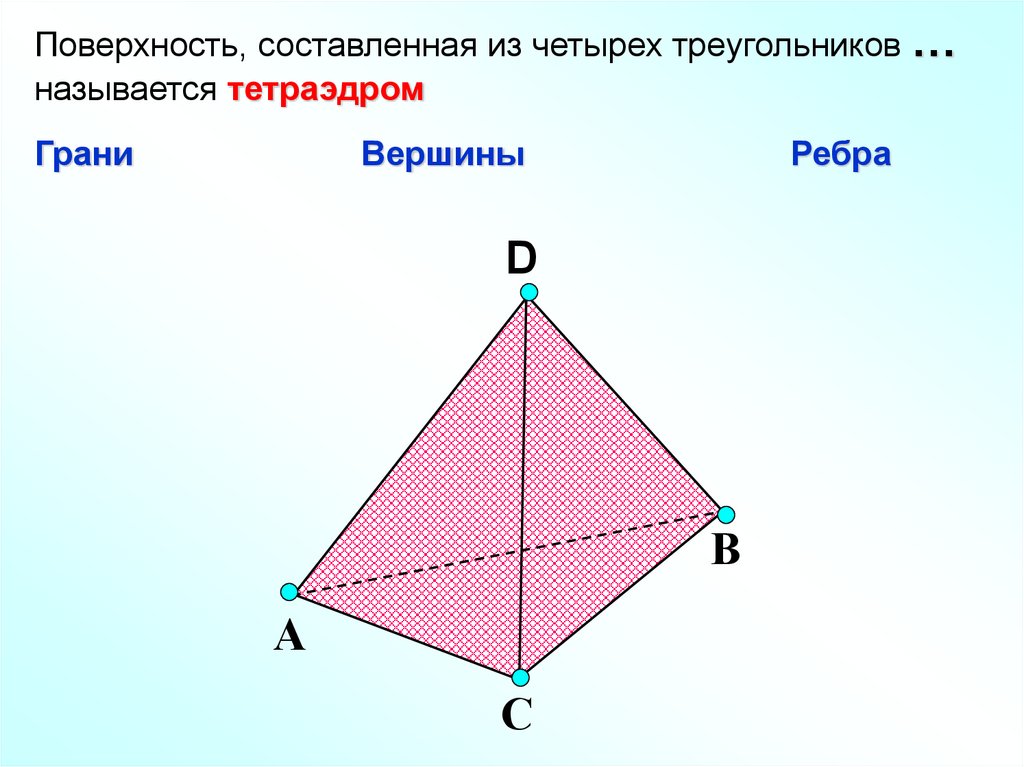
Поверхность, составленная из четырех треугольников …
называется тетраэдром
Грани
Вершины
Ребра
D
В
А
С

2.

Тетраэдр.
Слово составлено из греческих
«четыре»
и
- «основание».
,/
Буквальное значение – «четырехгранник».
По-видимому, термин впервые
S
S
употреблен Евклидом.
После Платона чаще
встречается «пирамида»
В
А
С

3.

Противоположные ребра
D
D
В
В
А
А
С
основание
С

4.

Тетраэдр – поверхность,
составленная из четырех
треугольников.
SS
В
А
С
Поверхность, составленную из многоугольников и
ограничивающую некоторое геометрическое тело, будем
называть многогранной поверхностью или многогранником.

5.

Параллелепипед –
поверхность, составленная из
шести параллелограммов.

6.

Параллелепипед АВСDA1B1C1D1 – поверхность,
составленная из двух равных параллелограммов АВСD и
A1B1C1D1 и четырех параллелограммов АВВ1А1, ADD1A1,
CDD1C1 и ВСС1В1
A1
D
1
B1
С1
D
А
В
С

7.

Параллелепипед АВСDA1B1C1D1
Грани
Противоположные грани
Вершины
A1
Ребра
D1
B1
С1
D
А
В
С

8.

Параллелепипед.
Слово составлено из греческих
,
«плоскость»
«поверхность».
,
Слово встречалось у Эвклида
и Герона, но его еще
не было у Архимеда.

9.

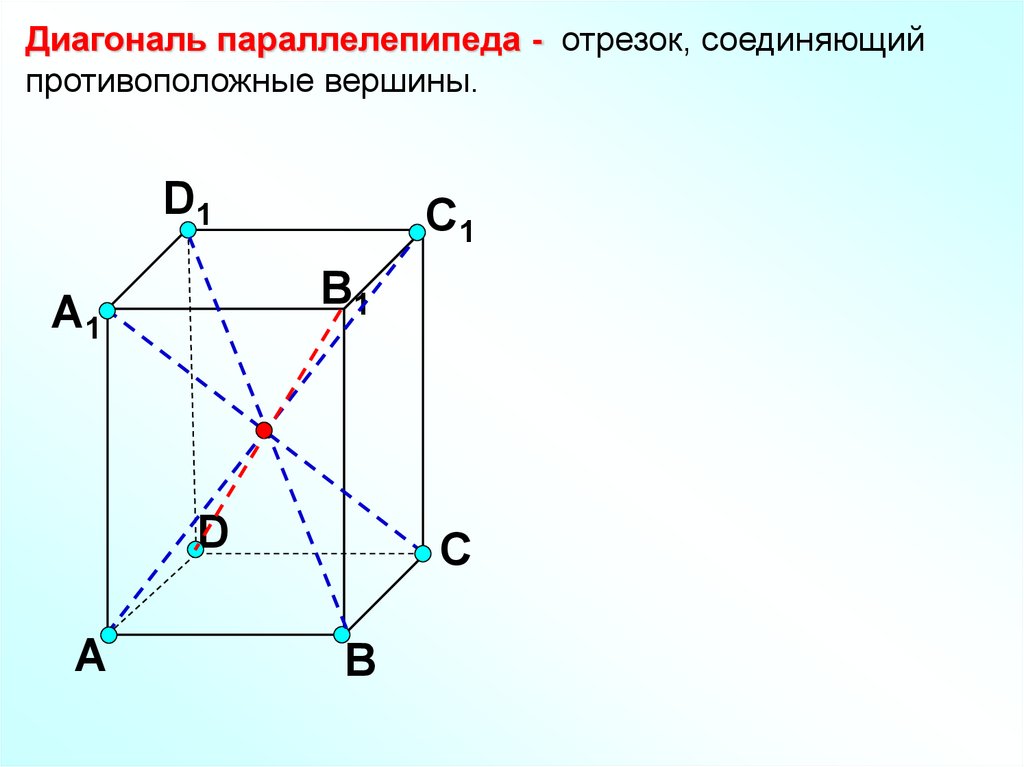
Диагональ параллелепипеда - отрезок, соединяющий
противоположные вершины.
D1
С1
B1
А1
D
А
С
В

10.

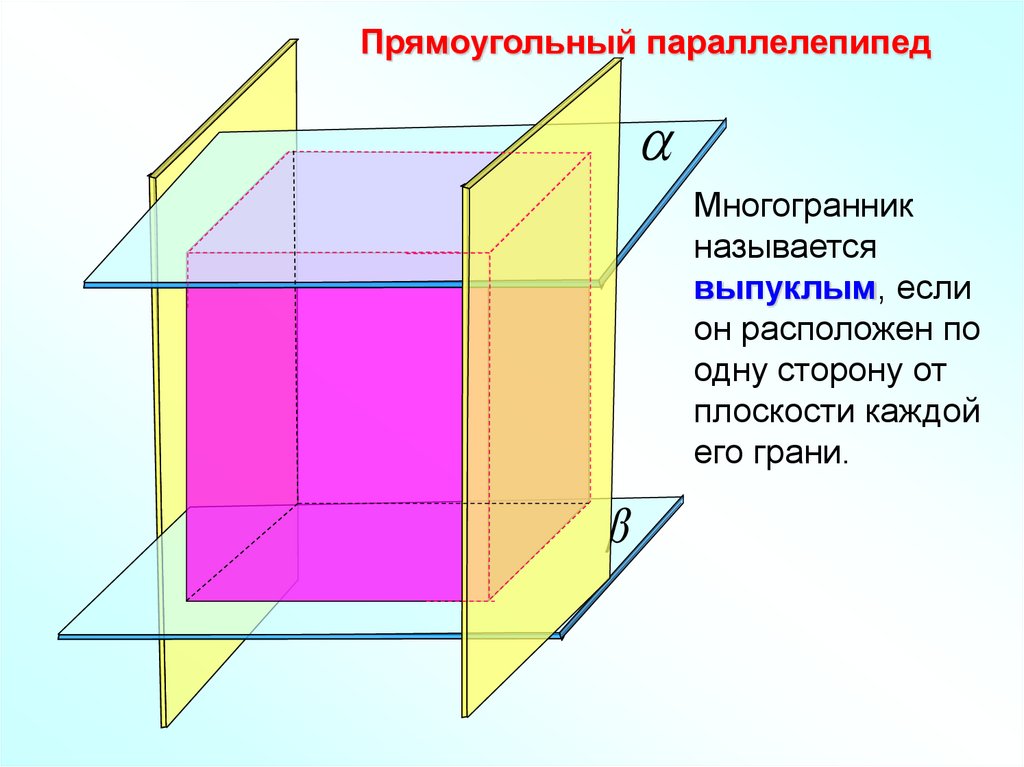
Прямоугольный параллелепипед
Многогранник
называется
выпуклым, если
он расположен по
одну сторону от
плоскости каждой
его грани.

11.

12.

многогранники
Однородные
невыпуклые
Однородные
выпуклые
Тела
Платона
Тела
Архимеда
Выпуклые
призмы и
антипризмы
Тела
КеплераПуансо
Невыпуклые
призмы и
антипризмы
Невыпуклые
полуправильные
однородные
многогранники

13.

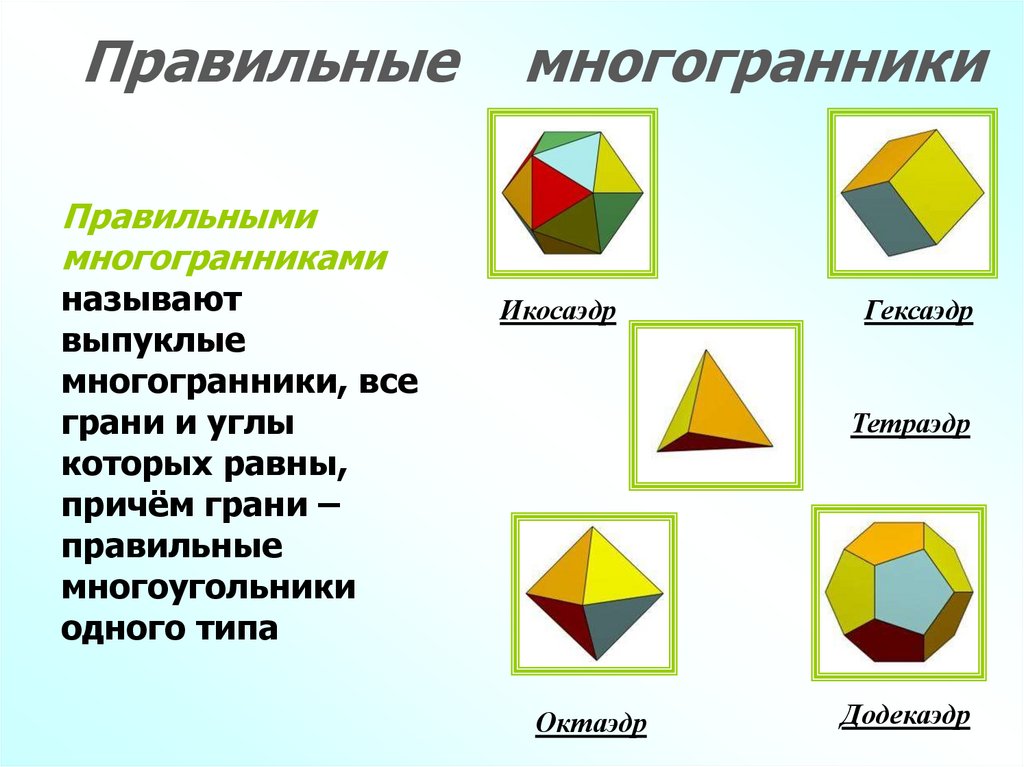
Правильные
многогранники
Правильными
многогранниками
называют
выпуклые
многогранники, все
грани и углы
которых равны,
причём грани –
правильные
многоугольники
одного типа
Икосаэдр
Гексаэдр
Тетраэдр
Октаэдр
Додекаэдр

14.

Невыпуклый многогранник

15.

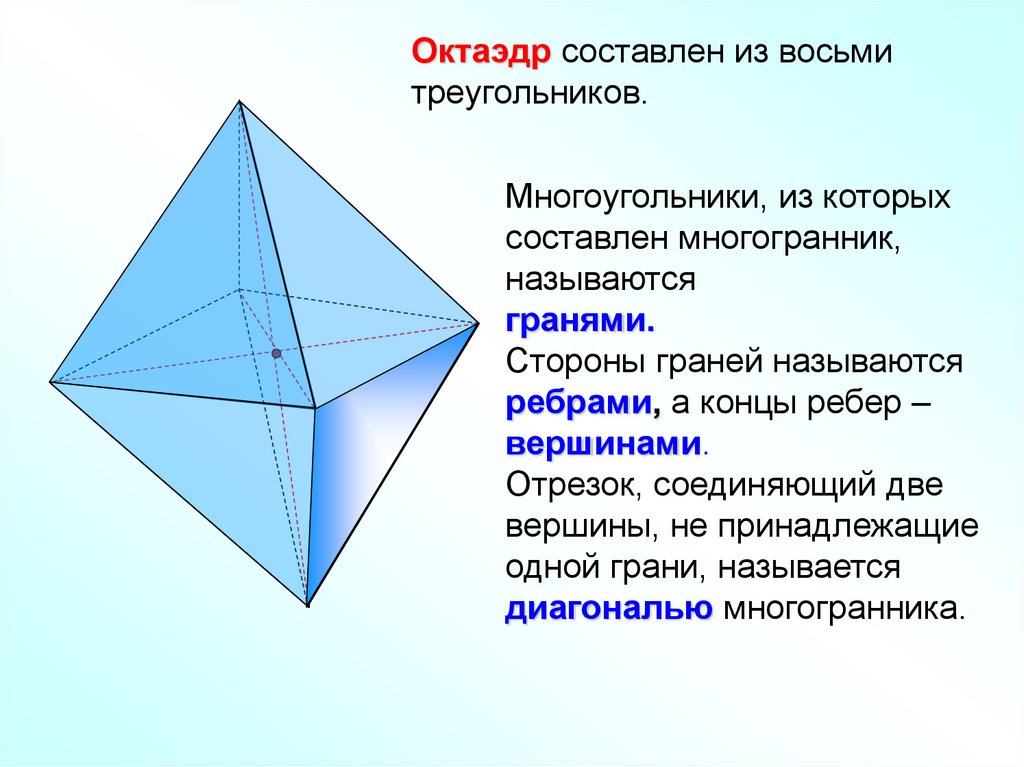
Октаэдр составлен из восьми
треугольников.
Многоугольники, из которых
составлен многогранник,
называются
гранями.
Стороны граней называются
ребрами, а концы ребер –
вершинами.
Отрезок, соединяющий две
вершины, не принадлежащие
одной грани, называется
диагональю многогранника.

16.

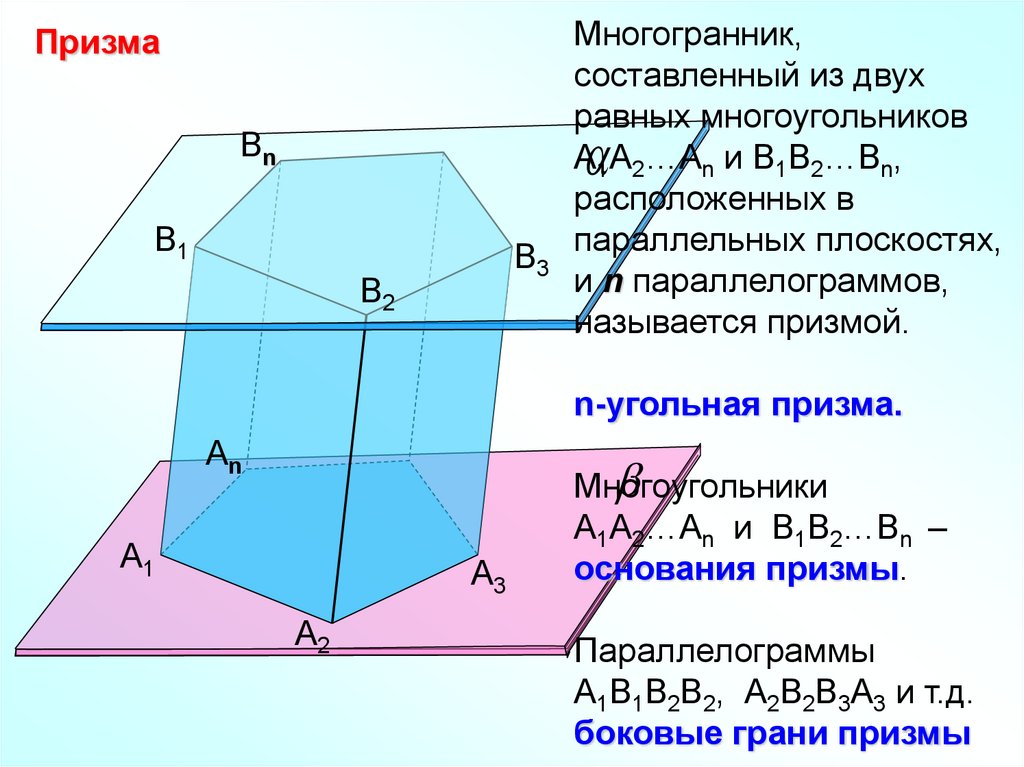
Призма
Многогранник,
составленный из двух
равных многоугольников
А1А2…Аn и В1В2…Вn,
расположенных в
параллельных плоскостях,
и n параллелограммов,
называется призмой.
Bn
B1
B3
B2
n-угольная призма.
Аn
А1
А3
А2
Многоугольники
А1А2…Аn и В1В2…Вn –
основания призмы.
Параллелограммы
А1В1В2В2, А2В2В3А3 и т.д.
боковые грани призмы

17.

Отрезки А1В1, А2В2 и т.д. боковые ребра призмы
Призма
Bn
Перпендикуляр,
проведенный из какойB3 нибудь точки одного
основания к плоскости
другого основания,
называется высотой
призмы.
B1
B2
Аn
А1
А3
А2

18.

Если боковые ребра перпендикулярны к основаниям, то
призма называется прямой, в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.

19.

Прямая призма называется правильной, если ее основания
- правильные многоугольники. У такой призмы все боковые
грани – равные прямоугольники.

20.

Изображение призмы с данным
многоугольником в основании:
провести из вершин
многоугольника параллельные
прямые
отложить на них равные
отрезки
соединить их концы в той же
последовательности, как и на
заданном основании

21.

Леонард Эйлер
(1701-1783)
Немецкий
математик и
физик
Формула Эйлера
(для правильных многогранников)
Г+В-Р=2

22.

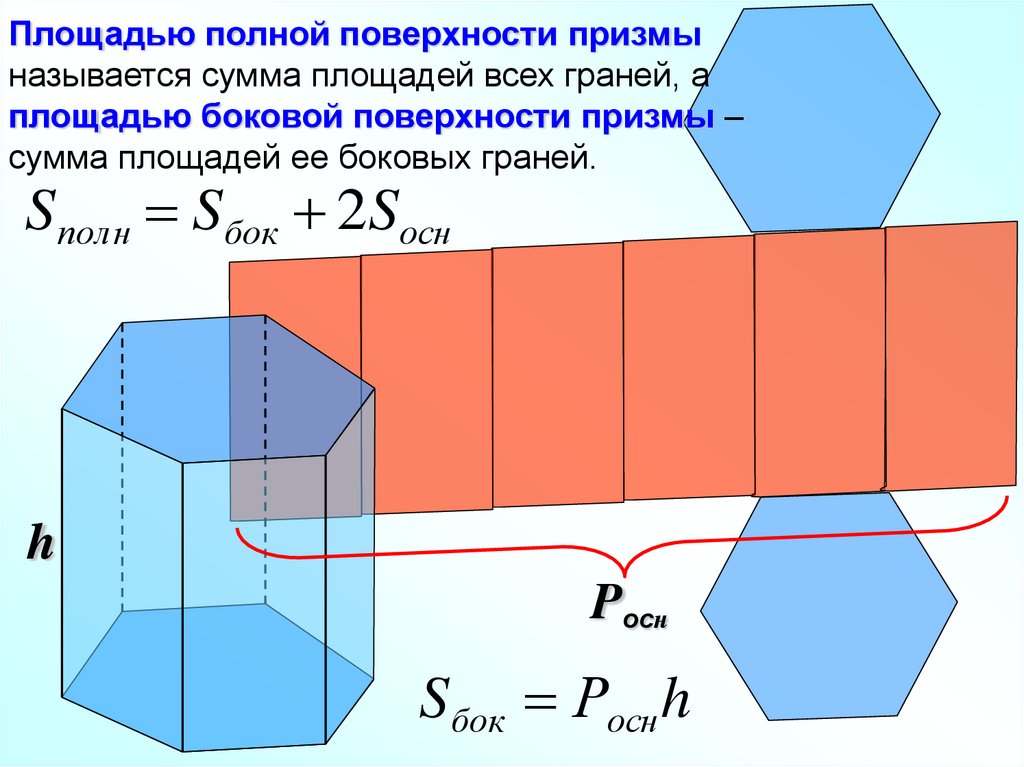
Площадью полной поверхности призмы
называется сумма площадей всех граней, а
площадью боковой поверхности призмы –
сумма площадей ее боковых граней.
Sполн Sбок 2Sосн
h
Pocн
Sбок Росн h

23.

№ 219.
В прямоугольном параллелепипеде стороны
основания равны 12 см и 5 см. Диагональ параллелепипеда
образует с плоскостью основания угол в 450. Найдите
боковое ребро параллелепипеда.
D1
С1
А1
В1
?
D
С
450
А
12 см
В

24.

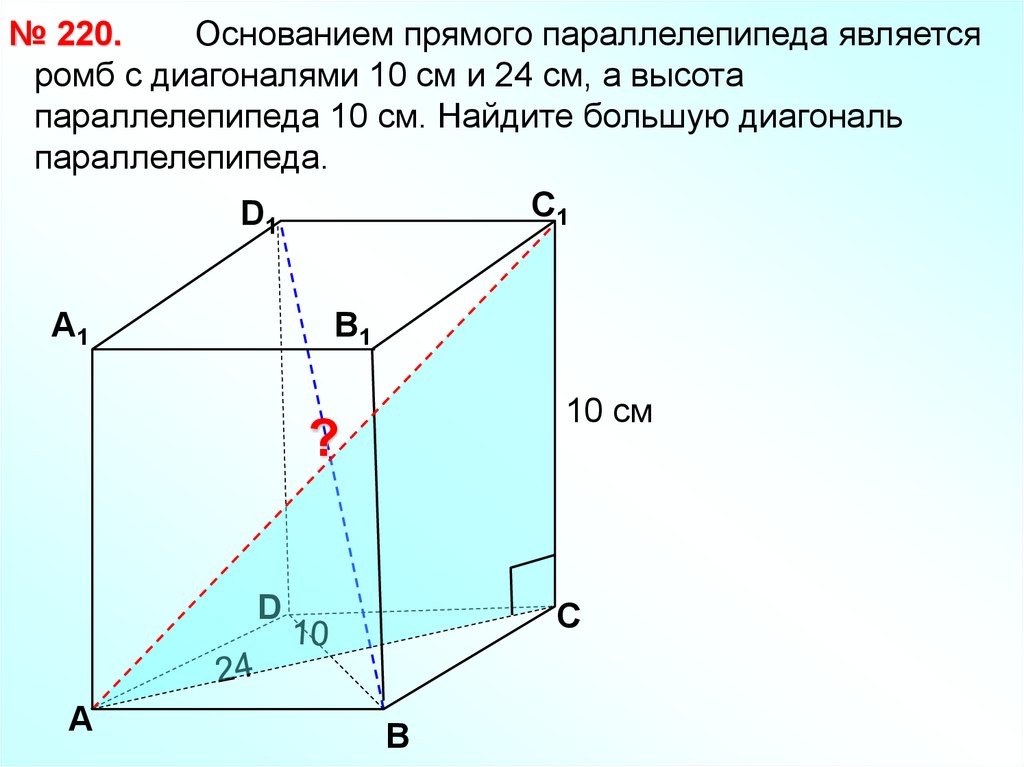
№ 220.
Основанием прямого параллелепипеда является
ромб с диагоналями 10 см и 24 см, а высота
параллелепипеда 10 см. Найдите большую диагональ
параллелепипеда.
С1
D1
А1
В1
10 см
?
D
А
С
В

25.

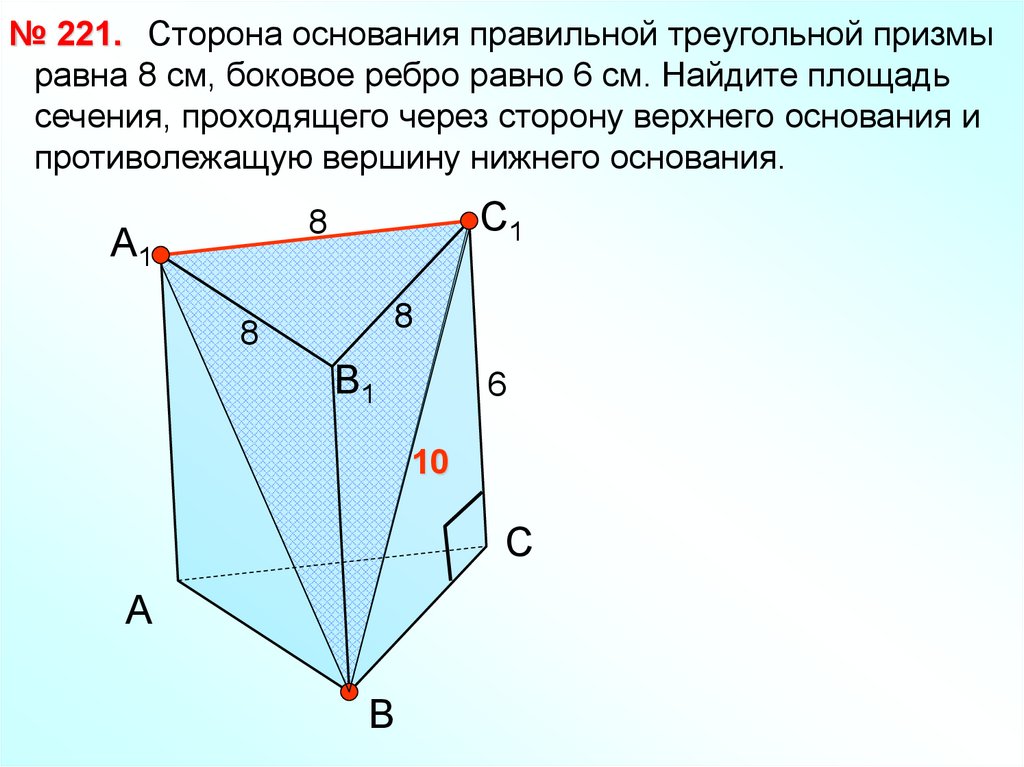
№ 221. Сторона основания правильной треугольной призмы
равна 8 см, боковое ребро равно 6 см. Найдите площадь
сечения, проходящего через сторону верхнего основания и
противолежащую вершину нижнего основания.
С1
8
А1
8
8
В1
6
10
С
А
В

26.

№ 222. Основанием прямой призмы является
равнобедренная трапеция с основаниями 25 см и 9 см и
высотой 8 см. Найдите двугранные углы при боковых ребрах
призмы.
D1
С1
А1
В1
D
9
С
25
F 8
8
А
8 H
В

27.

1. Сторона основания правильной треугольной
призмы равна 8 см, а диагональ боковой грани равна
10 см. Найдите площадь боковой и полной
поверхности призмы.
2. Основание прямой призмы – параллелограмм со
сторонами 8 и 15 см и углом 120о. Боковая
поверхность призмы имеет площадь 460 см2. Найдите
площадь сечения призмы, проходящего через боковое
ребро и меньшую диагональ основания.
3. Основание прямой призмы – прямоугольный
треугольник с катетами 13 и 12 см. Меньшая боковая
грань и основание призмы равновелики. Найдите
площадь боковой и полной поверхности призмы.

28.

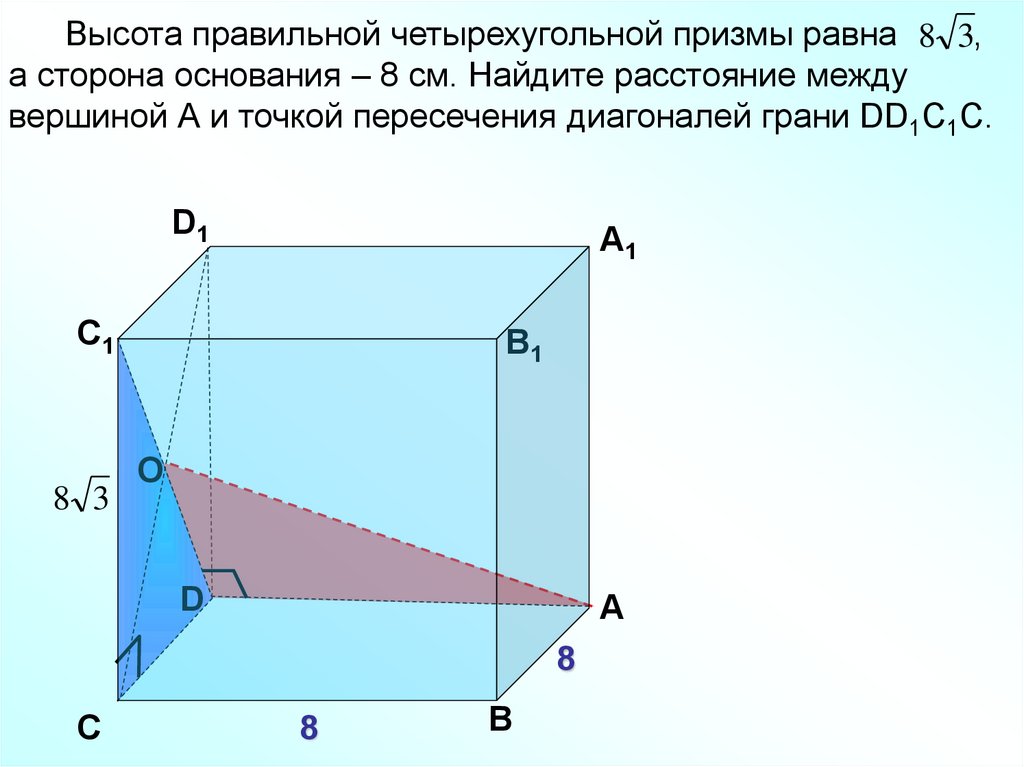
Высота правильной четырехугольной призмы равна 8 3,
а сторона основания – 8 см. Найдите расстояние между
вершиной А и точкой пересечения диагоналей грани DD1С1С.
D1
А1
С1
8 3
В1
О
D
А
8
С
8
В

29.

№ 223. Через два противолежащих ребра проведено
сечение, площадь которого равна 64 2 см2. Найдите ребро
куба и его диагональ.
D1
С1
В1
А1
a
S=
D
a
А
a
В
С

30.

№ 236. Докажите, что площадь боковой поверхности
наклонной призмы равна произведению периметра
перпендикулярного сечения на боковое ребро.
S1=A1A2* l
S2=A2A3* l
+ S =A A * l
3
A4
A1
l
3 4
S4=A4A1* l
Sбок Рсеч l
l
A2
A3

31.

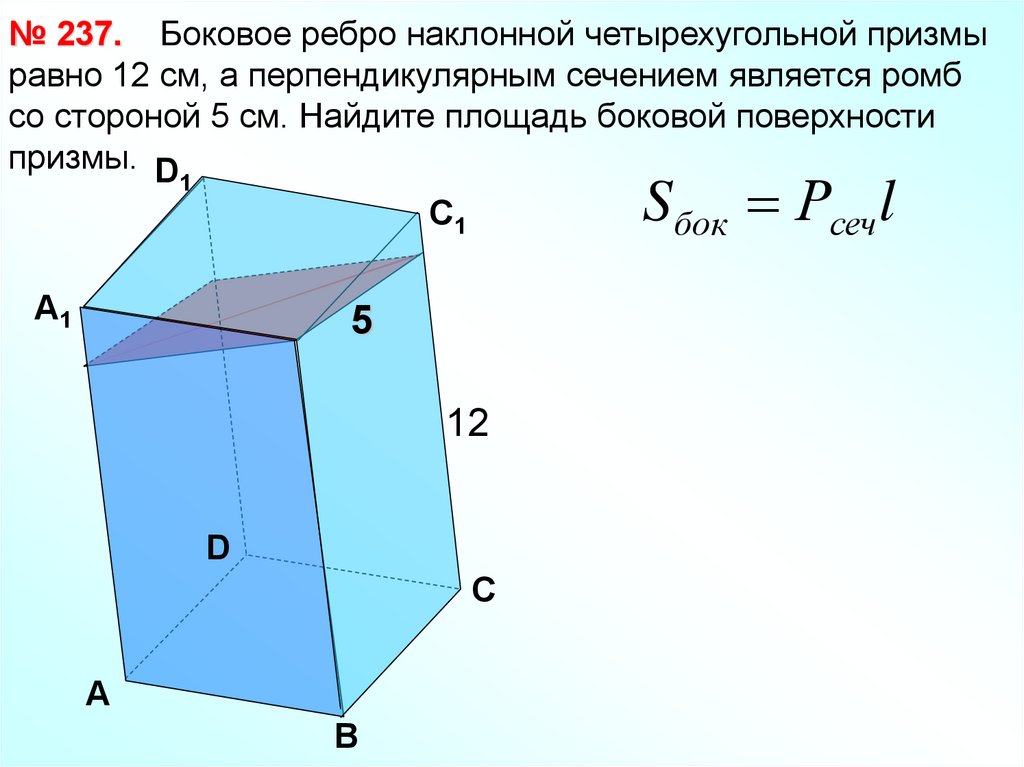
№ 237. Боковое ребро наклонной четырехугольной призмы
равно 12 см, а перпендикулярным сечением является ромб
со стороной 5 см. Найдите площадь боковой поверхности
призмы. D
1
Sбок Рсеч l
С1
А1
5
12
D
С
А
В

32.

№ 225. Диагональ правильной четырехугольной призмы
образует с плоскостью боковой грани угол в 300. Найдите угол
между диагональю и плоскостью основания.
a
D1
С1
А1
В1
2a
a
А
D
?
a
300
В
С

33.

№ 226. В правильной четырехугольной призме через
диагональ основания проведено сечение параллельно
диагонали призмы. Найдите площадь сечения, если сторона
основания призмы равна 2 см, а ее высота 4 см.
С1
D1
А1
В1
N
4
С
D
2
O
А
2
В

34.

№ 228. Основанием наклонной призмы АВСА1В1С1 является
равнобедренный треугольник АВС, в котором АС=АВ=13см,
ВС=10см,а боковое ребро призмы образует с плоскостью
основания угол в 450. Проекцией вершины А1 является точка
пересечения медиан треугольника АВС. Найдите площадь
грани СС1В1В.
А1
C1
B1
А
450
13
13
C
10
B

35.

№ 230. Основание прямой призмы – треугольник со
сторонами 5 см и 3 см и углом в 1200 между ними.
Наибольшая из площадей боковых граней равна 35 см2.
Найдите площадь боковой поверхности призмы.
С1
А1
В1
С
А
5
1200
В
3

36.

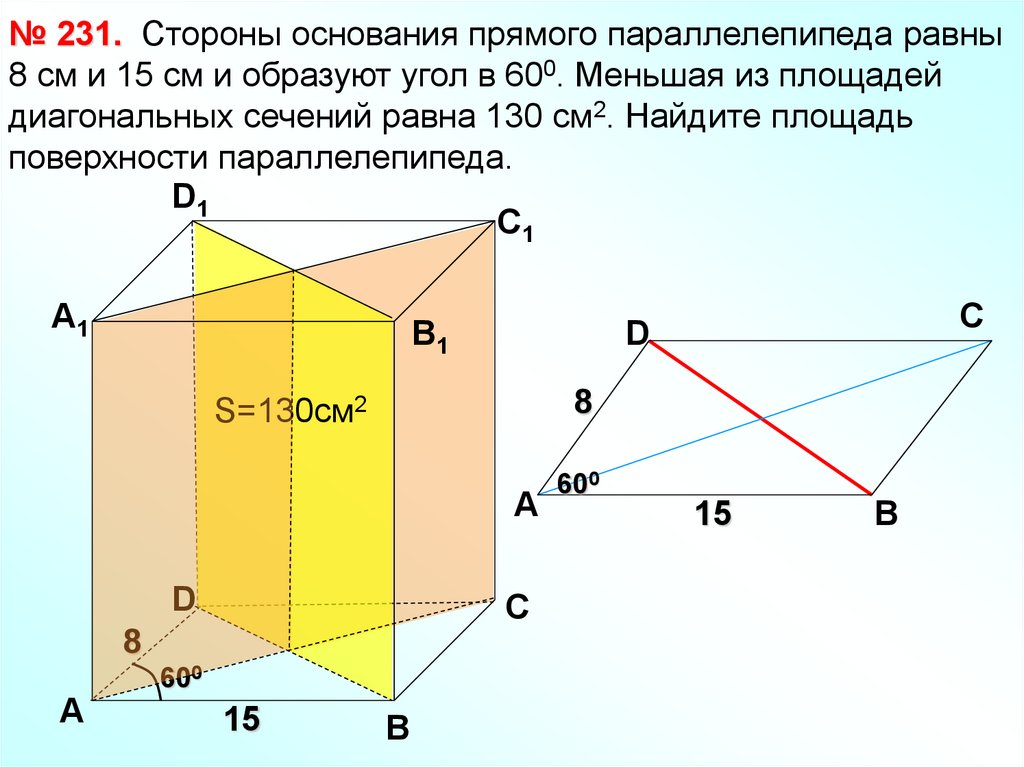
№ 231. Стороны основания прямого параллелепипеда равны
8 см и 15 см и образуют угол в 600. Меньшая из площадей
диагональных сечений равна 130 см2. Найдите площадь
поверхности параллелепипеда.
D1
С1
А1
В1
8
S=130см2
А
D
С
8
А
600
15
С
D
В
600
15
В

37.

№ 238. В наклонной треугольной призме две боковые грани
взаимно перпендикулярны, а их общее ребро, отстоящее от
двух других боковых ребер на 12 см и 35 см, равно 24 см.
Найдите площадь боковой поверхности призмы.
А1
C1
B1
35
О
А
К
12
C
B

38.

№ 232. Диагональ прямоугольного параллелепипеда,
равная d, образует с плоскостью основания угол , а с одной
из боковых граней – угол . Найдите площадь боковой
поверхности параллелепипеда.
D1
С1
А1
d
В1
D
А
С
В

39.

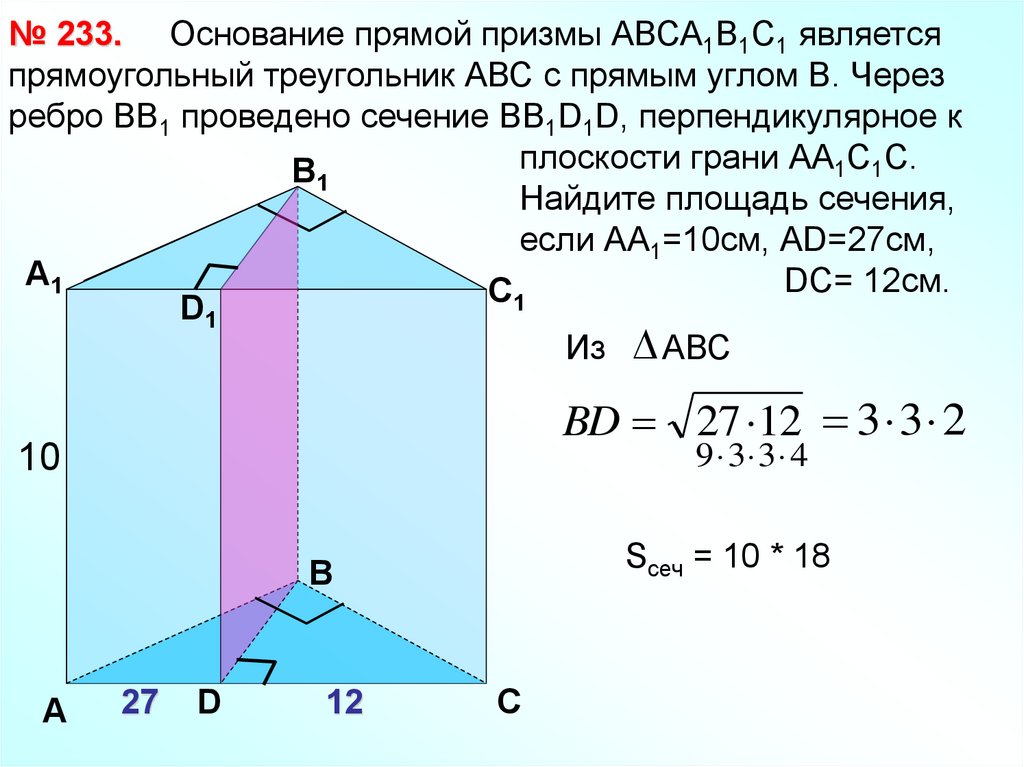
№ 233. Основание прямой призмы АВСА1В1С1 является
прямоугольный треугольник АВС с прямым углом В. Через
ребро ВВ1 проведено сечение ВВ1D1D, перпендикулярное к
плоскости грани АА1С1С.
В1
Найдите площадь сечения,
если АА1=10см, АD=27см,
А1
DC= 12см.
С
1
D
1
Из
BD 27 12 3 3 2
9 3 3 4
10
Sсеч = 10 * 18
В
А
АВС
27
D
12
С

40.

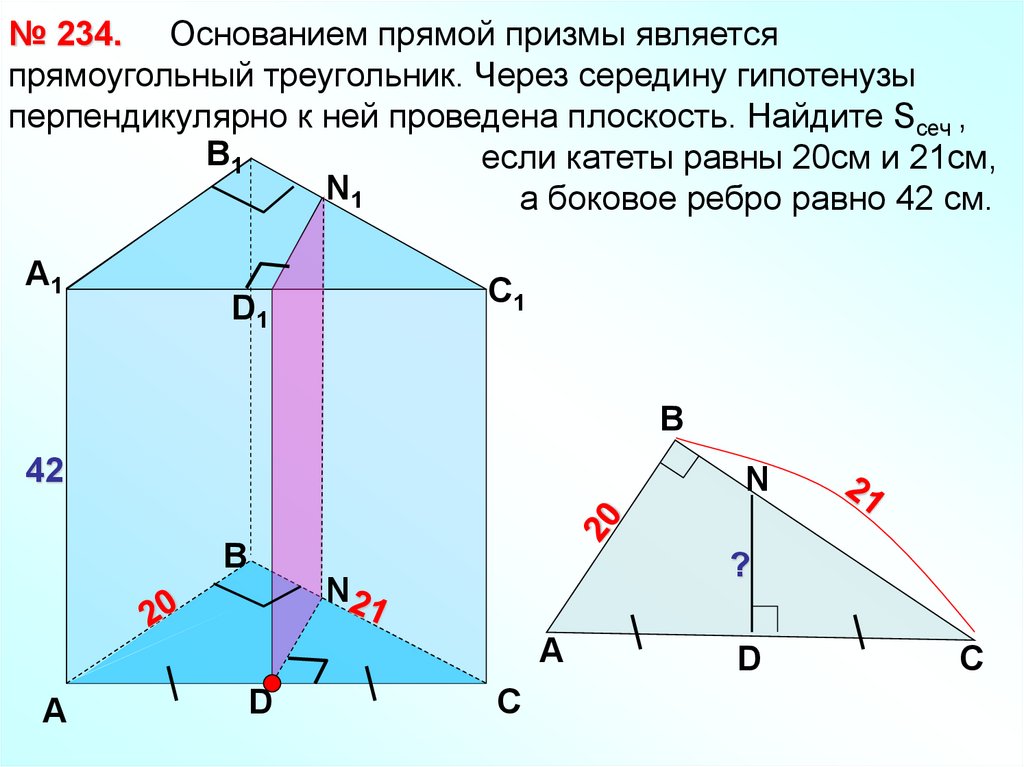
№ 234. Основанием прямой призмы является
прямоугольный треугольник. Через середину гипотенузы
перпендикулярно к ней проведена плоскость. Найдите Sсеч ,
В1
если катеты равны 20см и 21см,
N1
а боковое ребро равно 42 см.
А1
С1
D1
В
42
N
В
?
N
А
А
D
С
D
С