Similar presentations:
Системы двух линейных уравнений с двумя переменными. Алгебра. 7 класс
1.
2.
Решением уравнения с двумянеизвестными называется пара
переменных, при подстановке
которых уравнение становится
верным числовым равенством.
2
3.
Основные понятияЕсли даны два линейных
переменными х и у:
уравнения
a1x + b1y + c1 = 0
а2х + b2y + с2 = 0
с
двумя
и поставлена задача – найти такие пары значений
(х; у), которые одновременно удовлетворяют и
тому, и другому уравнению, то говорят, что
заданные уравнения образуют систему уравнений.
a1x + b1y + c1 = 0,
а2х + b2y + с2 = 0.
4.
Основные понятияПару значений (х; у), которая одновременно является
решением и первого, и второго уравнений системы,
называют решением системы.
Решить систему – это значит найти все ее
решения или установить, что их нет.
Пример:
x y 5 0,
2 x y 4 0.
5.
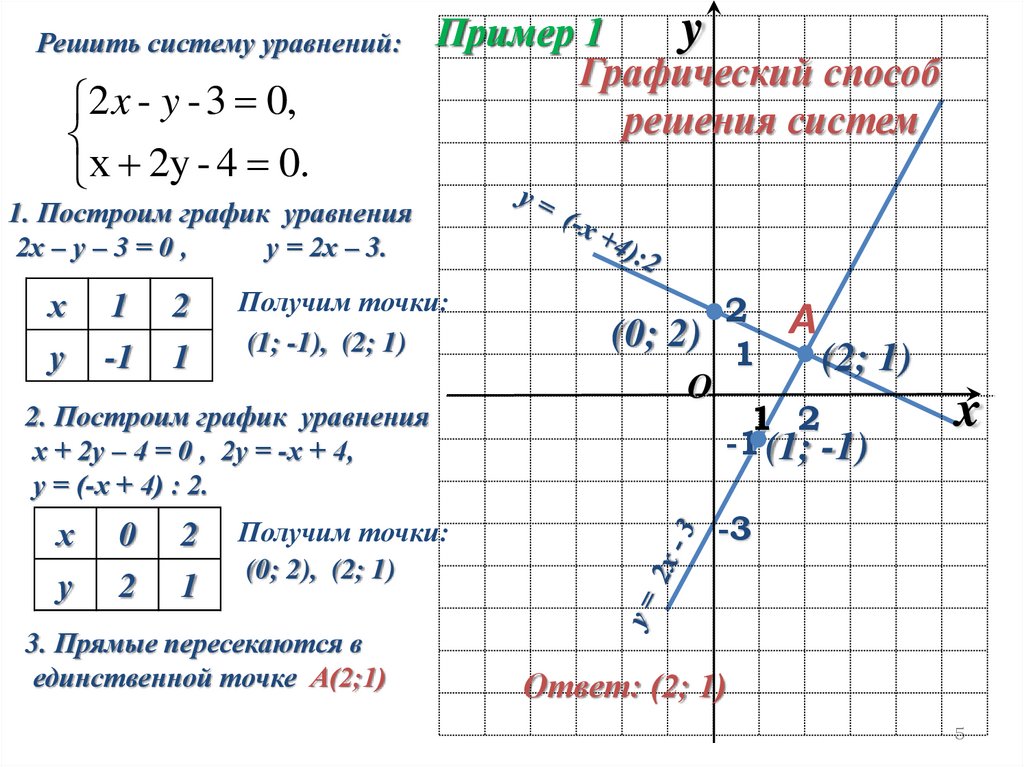
Решить систему уравнений:2 x - y - 3 0,
х 2y - 4 0.
y
Пример 1
Графический способ
решения систем
1. Построим график уравнения
2х – у – 3 = 0 ,
у = 2х – 3.
х
1
2
у
-1
1
Получим точки:
(1; -1), (2; 1)
2. Построим график уравнения
х + 2у – 4 = 0 , 2у = -х + 4,
у = (-х + 4) : 2.
х
0
2
у
2
1
Получим точки:
(0; 2), (2; 1)
3. Прямые пересекаются в
единственной точке А(2;1)
2 А
(0; 2) 1
(2; 1)
O
1 2
-1 (1; -1)
x
-3
Ответ: (2; 1)
5
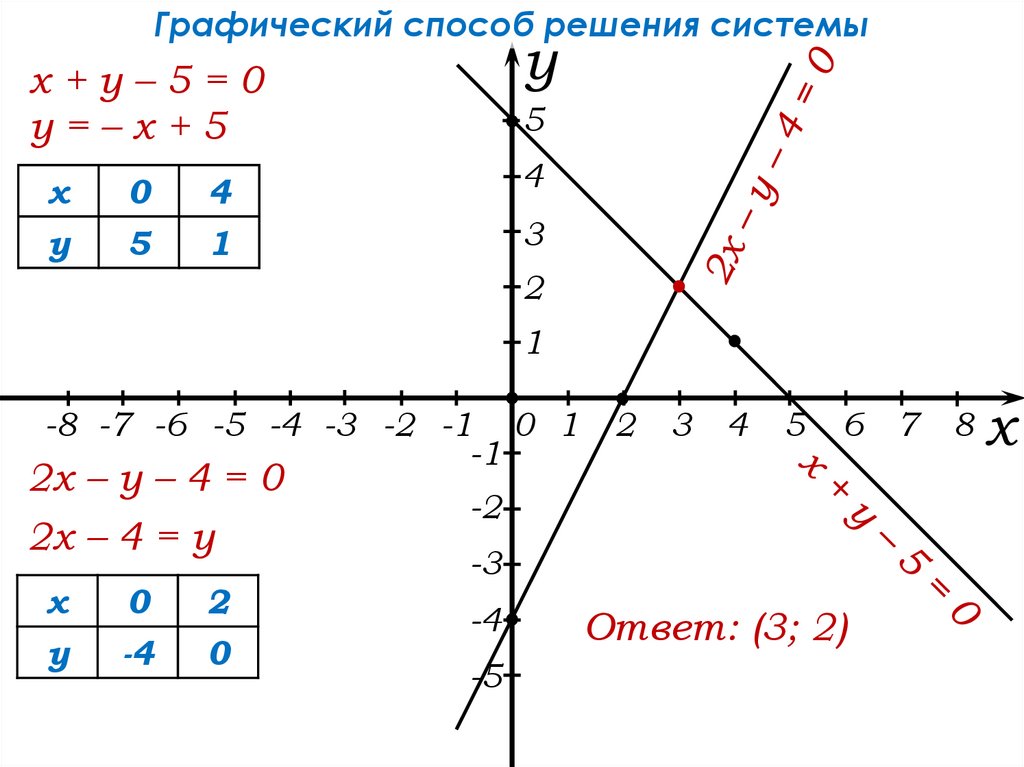
6.
Графический способ решения системыу
х+у–5=0
у=–х+5
х
у
0
5
5
4
4
1
3
2
1
-8 -7 -6 -5 -4 -3 -2 -1 0 1
-1
2х – у – 4 = 0
2х – 4 = у
х
0
2
у
-4
0
2
3
4
5
6 7
-2
-3
-4
-5
Ответ: (3; 2)
8
х
7.
Алгоритм решения системы уравненийграфическим способом
1. Приводим оба уравнения к виду линейной
функции y = k x + m.
2. Составляем расчётные таблицы для
каждой функции.
3. Строим графики функций в одной
координатной плоскости.
4. Определяем число решений:
• Если прямые пересекаются, то одно решение
пара чисел (х ; у) – координаты точки
пересечения;
• Если прямые параллельны, то нет решений;
• Если прямые совпадают, то бесконечно
много решений.
5. Записываем ответ.
8.
Алгоритм решения системыуравнений способом подстановки
o Из любого уравнения выразить x или y
(например: y из 1 уравнения).
o В другое уравнение вместо выраженной
переменной (y) подставить полученное
буквенное выражение .
o Получилось уравнение с одной переменной
(x). Решив его, найти значение переменной
(x).
o Подставить найденное значение переменной
(x) в выражение, определённое на первом
шаге (например: y). Вычислить значение
другой переменной (y).
9.
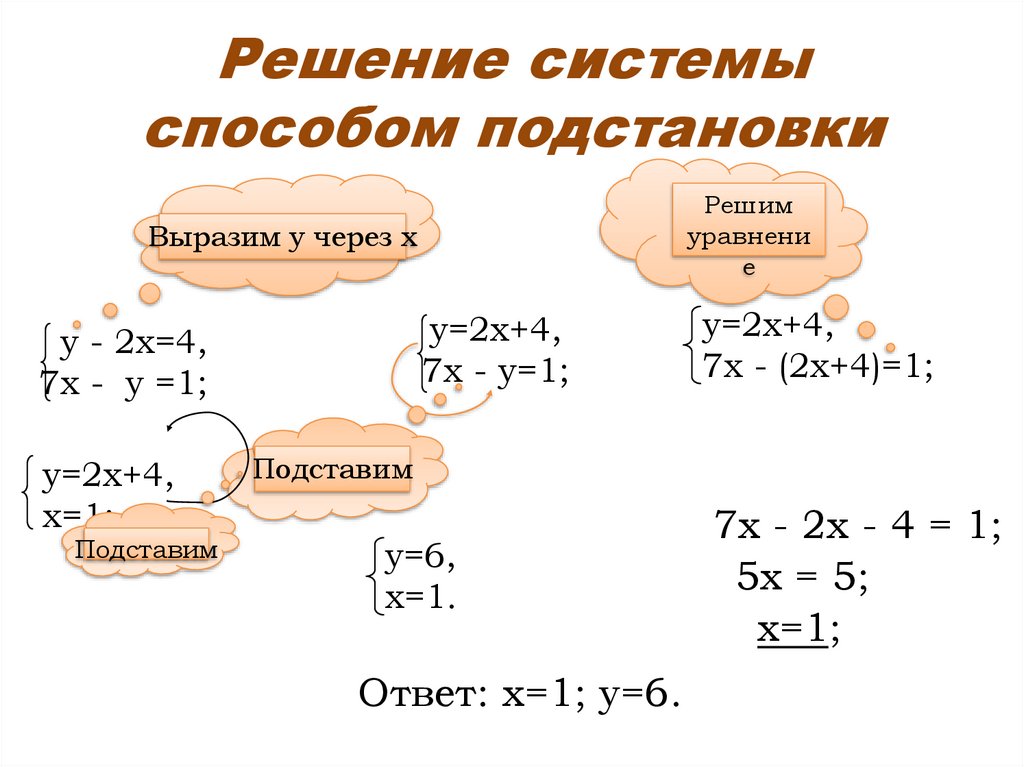
Решение системыспособом подстановки
Решим
уравнени
е
Выразим у через х
у=2х+4,
7х - у=1;
у - 2х=4,
7х - у =1;
у=2х+4,
х=1;
Подставим
у=2х+4,
7х - (2х+4)=1;
Подставим
у=6,
х=1.
Ответ: х=1; у=6.
7х - 2х - 4 = 1;
5х = 5;
х=1;
10.
Метод подстановки решения системы двухлинейных уравнений с двумя переменными
3x y 2 0,
2 x y 5 0.
2x 3х 2 5 0
y 3x 2,
2x 3х 2 5 0;
5x 3
x 0,6,
y 3,8.
2x 3х 2 5 0
x 0,6
y 3 0,6 2 3,8
Ответ : 0,6; 3,8 .
11.
Метод подстановки решения системы двухлинейных уравнений с двумя переменными
5 11 12 у 3 у 8 0;
55 60 у 3 у 8 0;
55
8
60
у
3
у
;
5 11 12 у 3 у 8 0,
63 63 у;
x
11
12
у
;
у 1.
x 1,
х 11 12 1 1.
y 1.
5 x 3 y 8 0,
x 12 y 11;
Ответ : 1; 1 .








 mathematics
mathematics








