Similar presentations:
Системы двух линейных уравнений с двумя переменными. 7 класс
1.
Урок № 32Основные понятия.
1
2.
Сформировать представление о математическоймодели система уравнений.
Познакомиться с понятием системы двух
линейных уравнений и ее решении.
Изучить графический способ решения систем двух
уравнений.
Решить вопрос о количестве решений системы
двух линейных уравнений с двумя переменными.
Решение более сложных систем двух уравнений с
двумя неизвестными.
27.03.2020
2
3.
Вспомним!1.
2.
3.
4.
5.
6.
7.
8.
Что называется линейным уравнением с двумя неизвестными?
Что значит решить уравнение с двумя неизвестными?
Сколько может быть решений у линейного уравнения?
Что называется графиком линейного уравнения с двумя
переменными?
Сколько точек определяет прямую?
Когда две прямые на плоскости пересекаются?
Когда две прямые на плоскости параллельны?
Когда две прямые на плоскости совпадают?
27.03.2020
3
4.
Вспомним!Решением уравнения с двумя
неизвестными называется пара
переменных, при подстановке
которых уравнение становится
верным числовым равенством.
27.03.2020
4
5.
Решить линейное уравнение –это значит найти те значения
переменной, при каждом из которых
уравнение обращается в верное
числовое равенство.
Таких решений бесконечно много.
27.03.2020
5
6.
27.03.20206
7.
входит в уравнениеобязательно в
5x-8=0
2х² + 3х + 7 = 0
27.03.2020
7
8.
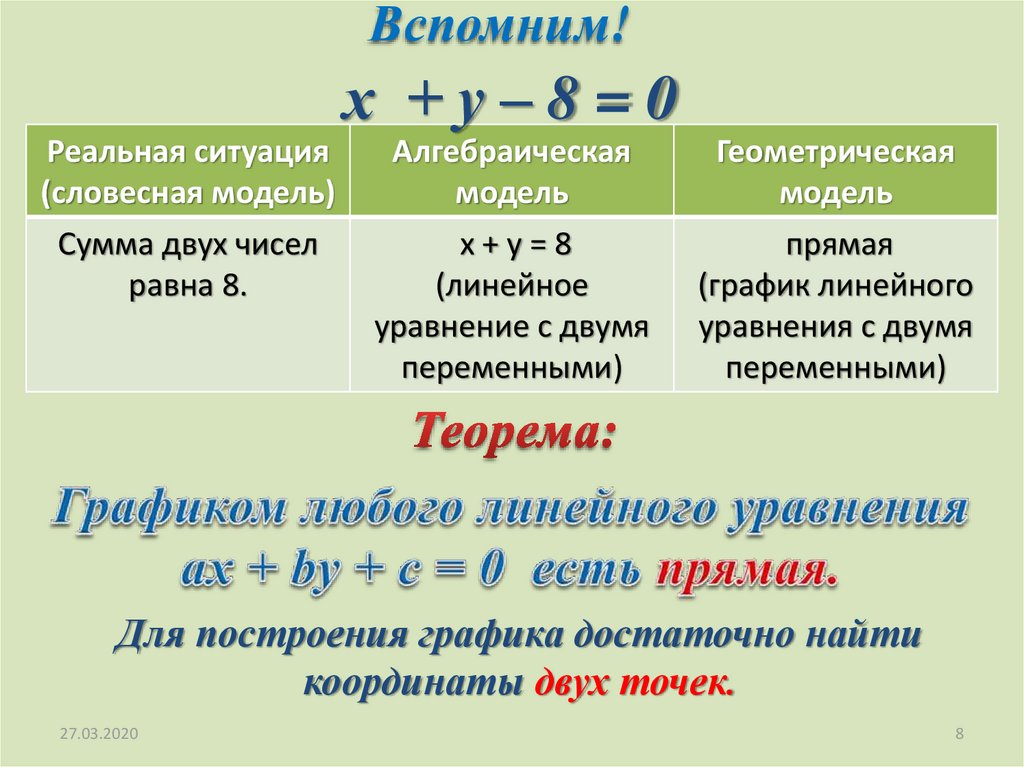
Вспомним!х +у–8=0
Реальная ситуация
(словесная модель)
Сумма двух чисел
равна 8.
Алгебраическая
модель
х+у=8
(линейное
уравнение с двумя
переменными)
Геометрическая
модель
прямая
(график линейного
уравнения с двумя
переменными)
Для построения графика достаточно найти
координаты двух точек.
27.03.2020
8
9.
Вспомним!1. Придать переменной х конкретное значение х₁; найти
из уравнения ах + bу + c = 0 соответствующее значение у₁.
Получим (х₁;у₁).
2. Придать переменной х конкретное значение х₂; найти
из уравнения ах + bу + c = 0 соответствующее значение у₂.
Получим (х₂;у₂).
3. Построим на координатной плоскости точки (х₁; у₁),
(х₂; у₂) и соединим прямой.
4. Прямая – есть график уравнения.
27.03.2020
9
10.
Количество болезнетворных микробов в организмеописывается по формуле y-50000=5000t. Человек
начинает принимать лекарство. Количество
микробов, уничтожаемых лекарством, y=15000t (t –
время в сутках). Какое время человек должен
принимать лекарство?
27.03.2020
10
11.
Часто приходится рассматривать математическую модельсостоящую из двух линейных уравнений с двумя переменными.
a1 x b1 y c1 0
a 2 х b 2 y c 2 0
Решение системы уравнений с двумя неизвестными
называется пара переменных, при подстановке
которых уравнения становятся верными числовыми
равенствами.
Решить систему - это значит найти все ее решения
или доказать, что их нет.
27.03.2020
11
12.
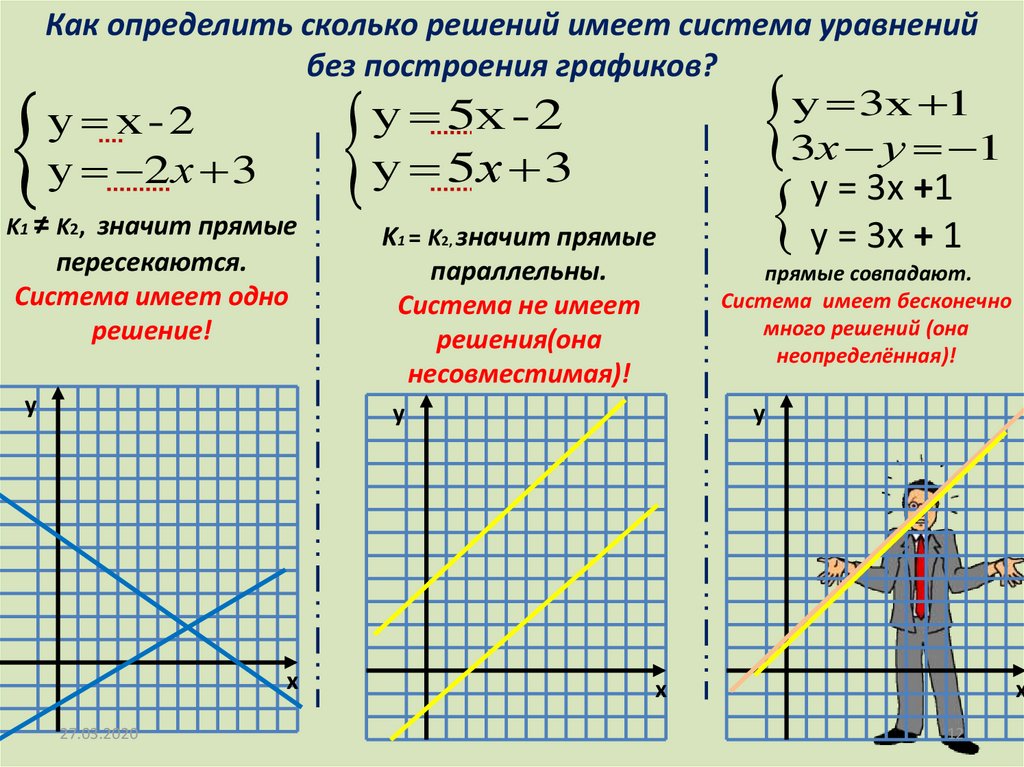
Как определить сколько решений имеет система уравненийбез построения графиков?
у х -2
у 2 х 3
K1 ≠ K2, значит прямые
пересекаются.
Система имеет одно
решение!
y
у 3х 1
3х у 1
у 5х - 2
у 5х 3
K1 = K2, значит прямые
параллельны.
Система не имеет
решения(она
несовместимая)!
y
x
27.03.2020
у = 3х +1
у = 3х + 1
прямые совпадают.
Система имеет бесконечно
много решений (она
неопределённая)!
y
x
x
12
13.
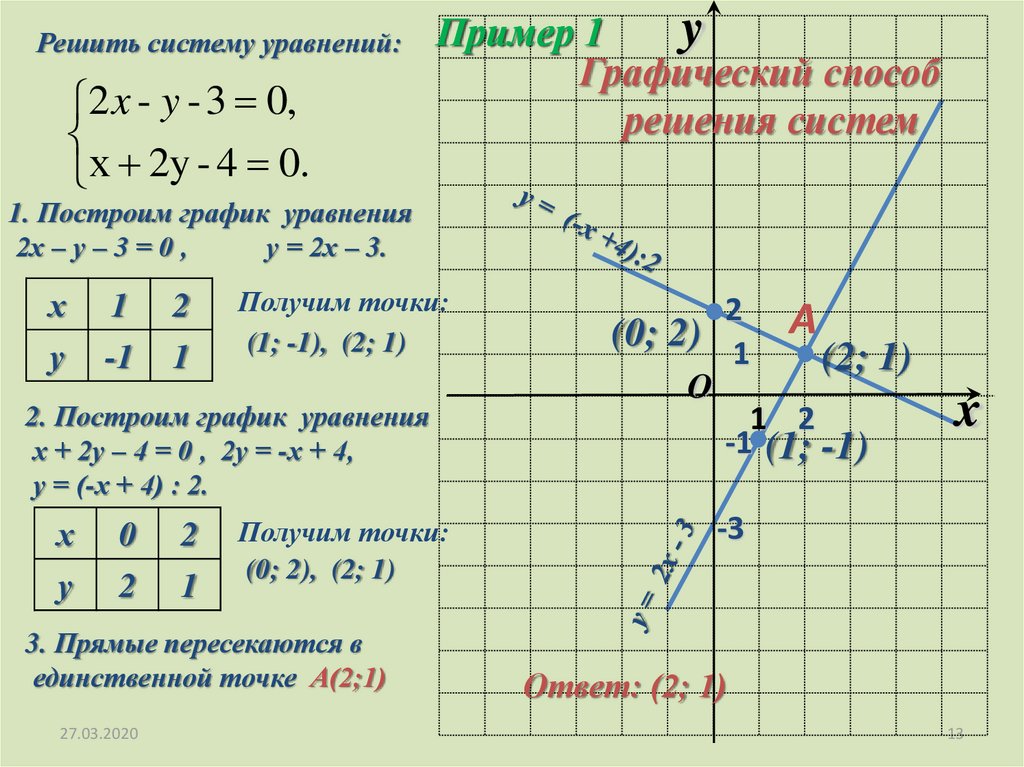
Решить систему уравнений:2 x - y - 3 0,
х 2y - 4 0.
y
Пример 1
Графический способ
решения систем
1. Построим график уравнения
2х – у – 3 = 0 ,
у = 2х – 3.
х
1
2
у
-1
1
Получим точки:
(1; -1), (2; 1)
2. Построим график уравнения
х + 2у – 4 = 0 , 2у = -х + 4,
у = (-х + 4) : 2.
х
0
2
у
2
1
Получим точки:
(0; 2), (2; 1)
3. Прямые пересекаются в
единственной точке А(2;1)
27.03.2020
2 А
(0; 2) 1
(2; 1)
O
1 2
-1 (1; -1)
x
-3
Ответ: (2; 1)
13
14. Алгоритм решения системы уравнений графическим способом
1. Приводим оба уравнения к виду линейной функцииy = k x + m.
2. Составляем расчётные таблицы для каждой
функции.
3. Строим графики функций в одной координатной
плоскости.
4. Определяем число решений:
• Если прямые пересекаются, то одно решение пара
чисел (х ; у) – координаты точки пересечения;
• Если прямые параллельны, то нет решений;
• Если прямые совпадают, то бесконечно много
решений.
5. Записываем ответ.
15.
Решить в тетради:1. № 1057 , 1061
27.03.2020
15
16.
Количество решений двух линейных уравнений сдвумя переменными.
a1 x b1 y c1 0
a 2 х b 2 y c 2 0
а1 b1
1 )Если
≠ , то прямые пересекаются и система
а 2 b2 имеет единственное решение.
а1 b1 c1
2 )Если
=
≠ , то прямые параллельны и система не
а 2 b2 c 2 имеет решений. Система называется
несовместной.
а1 b1 c1
3 )Если
=
= , то прямые совпадают и система
а 2 b2 c 2 имеет бесконечно много решений.
Система называется
неопределенной.
27.03.2020
16
17.
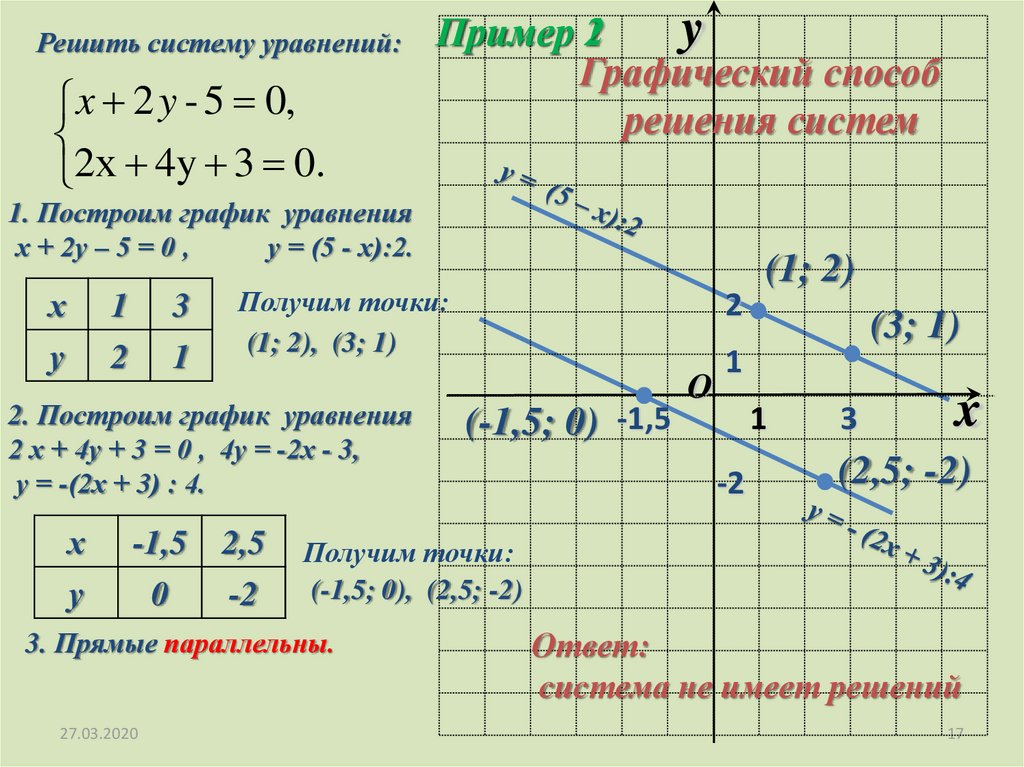
Решить систему уравнений:x 2 y - 5 0,
2х 4y 3 0.
y
Пример 2
1
Графический способ
решения систем
1. Построим график уравнения
х + 2у – 5 = 0 ,
у = (5 - х):2.
х
1
3
у
2
1
Получим точки:
(1; 2), (3; 1)
2. Построим график уравнения
2 х + 4у + 3 = 0 , 4у = -2х - 3,
у = -(2х + 3) : 4.
х
у
-1,5
0
2,5
-2
2
(-1,5; 0) -1,5
O
(3; 1)
1
1
-2
3
x
(2,5; -2)
Получим точки:
(-1,5; 0), (2,5; -2)
3. Прямые параллельны.
27.03.2020
(1; 2)
Ответ:
система не имеет решений
17
18.
Пример 3При каких значениях а система уравнений имеет единственное решение:
(2a - 1) x 3 y 7a 1,
(a 2)х 2y 5a - 3.
Условие при которых система уравнений имеет единственное решение:
2а - 1 3
≠ ,
а+2 2
Используем свойство пропорции:
2(2a - 1) ≠ 3(a + 2),
4a - 2 ≠ 3a + 6
4a - 3a ≠ 2 + 6
a≠8
27.03.2020
18
19.
Пример 4При каких значениях а система уравнений несовместна
(т.е. не имеет решений):
(2a - 1) x 3 y 7a 1,
(2a 1)х 5y 5a - 3.
Условие при которых система уравнений несовместна (не имеет решений):
2а - 1 3 7 a + 1
= ≠
2а + 1 5 5 a - 3
1) Сначала рассмотрим равенство
2а - 1 3
=
2а + 1 5
Используем свойство пропорции:
5(2a - 1) = 3(2a + 1),
10a - 5 = 6a + 3
27.03.2020
10a - 6a = 3 + 5
4a = 8
a=2
19
20.
2) Теперь проверим неравенство:При подстановке значения а = 2 имеем:
3 15
≠
5 7
27.03.2020
3 7a + 1
≠
5 5a - 3
3 7 •2+1
≠
5 5•2-3
- верное неравенство
20
21.
Пример 5При каких значениях а система уравнений неопределенна:
(2a - 1) x 3 y 7a 1,
(a 1)х 6y 11a 5.
Укажите решения системы.
Условие при которых система уравнений неопределенна:
2а - 1 3 7 a + 1
= =
а + 1 6 11a + 5
1) Сначала рассмотрим равенство
Используем свойство пропорции:
4a - 2 = a + 1
27.03.2020
2а - 1 3
=
а+1 6
2а - 1 1
=
а+1 2
2(2a - 1) = a + 1 ,
4a - a = 1 + 2
3a = 3
a=1
21
22.
2) Теперь проверим равенство:3 7a + 1
=
6 11a + 5
При подстановке значения а = 1 имеем:
1 1
=
2 2
3 7 •1+1
≠
6 11 • 1 + 5
- верное равенство
При подстановке значения а = 1 в данную систему имеем:
(2 1 - 1) x 3 y 7 1 1,
(1 1)х 6y 11 1 5.
Поделим второе уравнение на 2, имеем:
27.03.2020
x 3y 8,
2х 6y 16.
x 3y 8,
х 3y 8.
22
23.
1. Что собой представляют графики обоих уравненийсистемы?
2. В каком случае система имеет единственное решение?
3. Какая система является несовместимой?
4. О какой системе говорят, что она неопределенна?
5. Что называется решением системы уравнений с двумя
переменными?
6. Что значит решить систему уравнений?
27.03.2020
23
24.
1. Учебник: прочитать § 4042, с. 199‒211;2. Задачник:
№ 1028, 1045
27.03.2020
24



















 mathematics
mathematics








