Similar presentations:
Пропорциональные отрезки в прямоугольном треугольнике
1. Решение задач по теме: «Пропорциональные отрезки в прямоугольном треугольнике»
2.
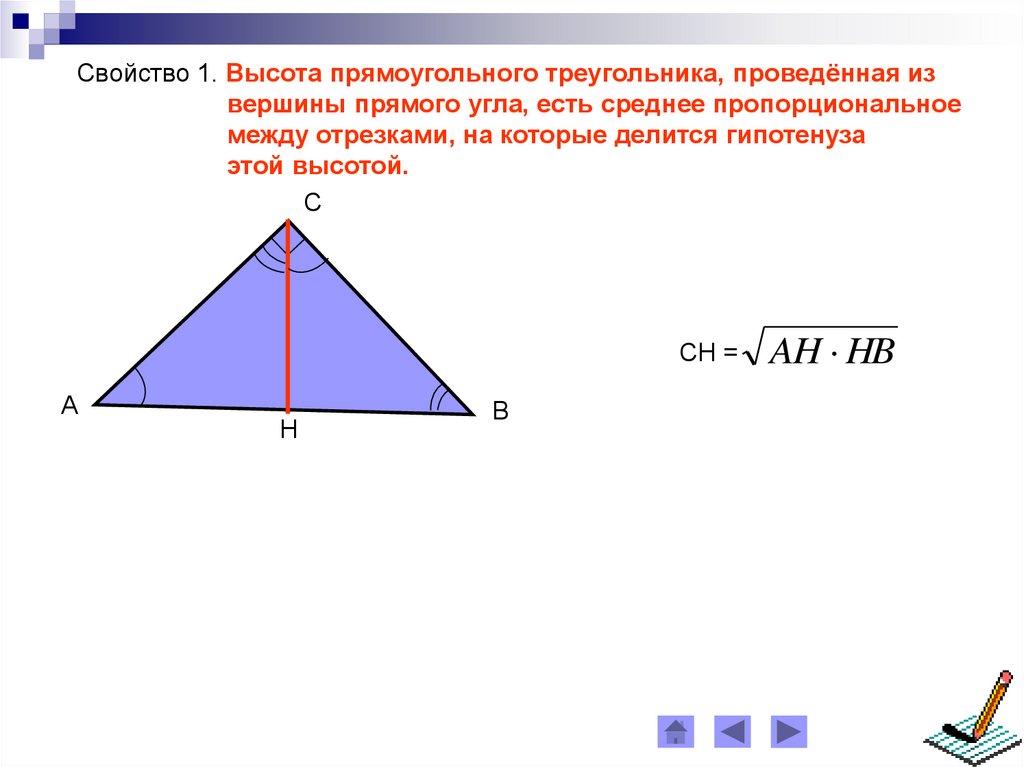
Свойство 1. Высота прямоугольного треугольника, проведённая извершины прямого угла, есть среднее пропорциональное
между отрезками, на которые делится гипотенуза
этой высотой.
С
СН =
А
Н
В
AH HB
3.
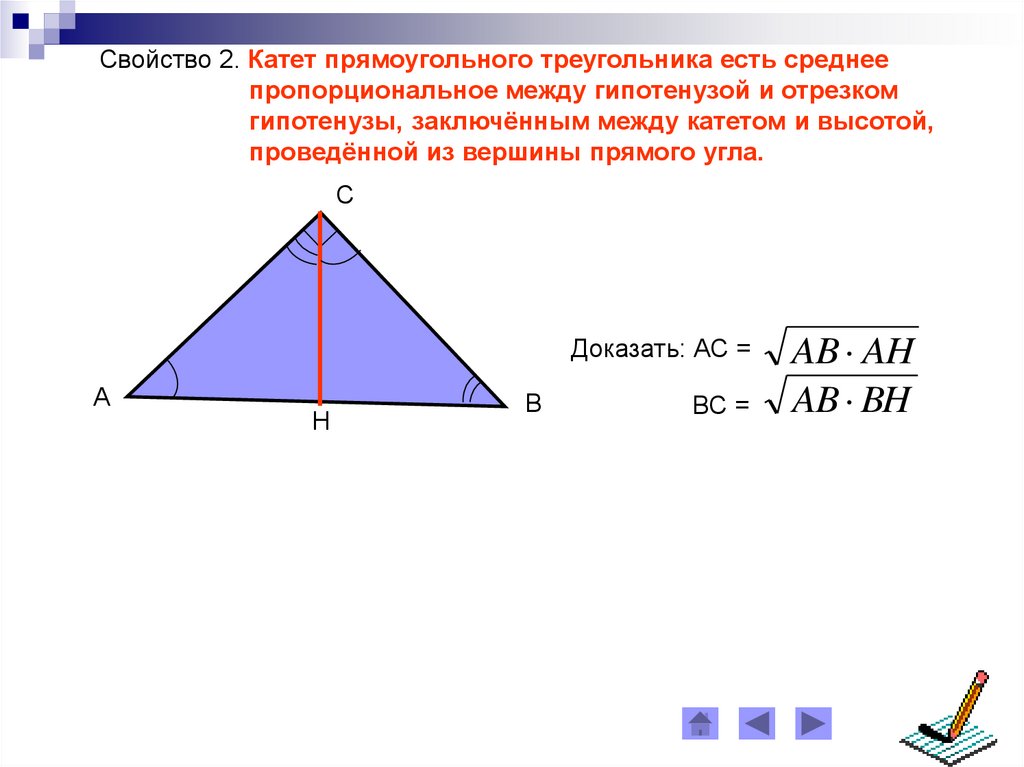
Свойство 2. Катет прямоугольного треугольника есть среднеепропорциональное между гипотенузой и отрезком
гипотенузы, заключённым между катетом и высотой,
проведённой из вершины прямого угла.
С
Доказать: АС =
А
Н
В
ВС =
AB AH
AB BH
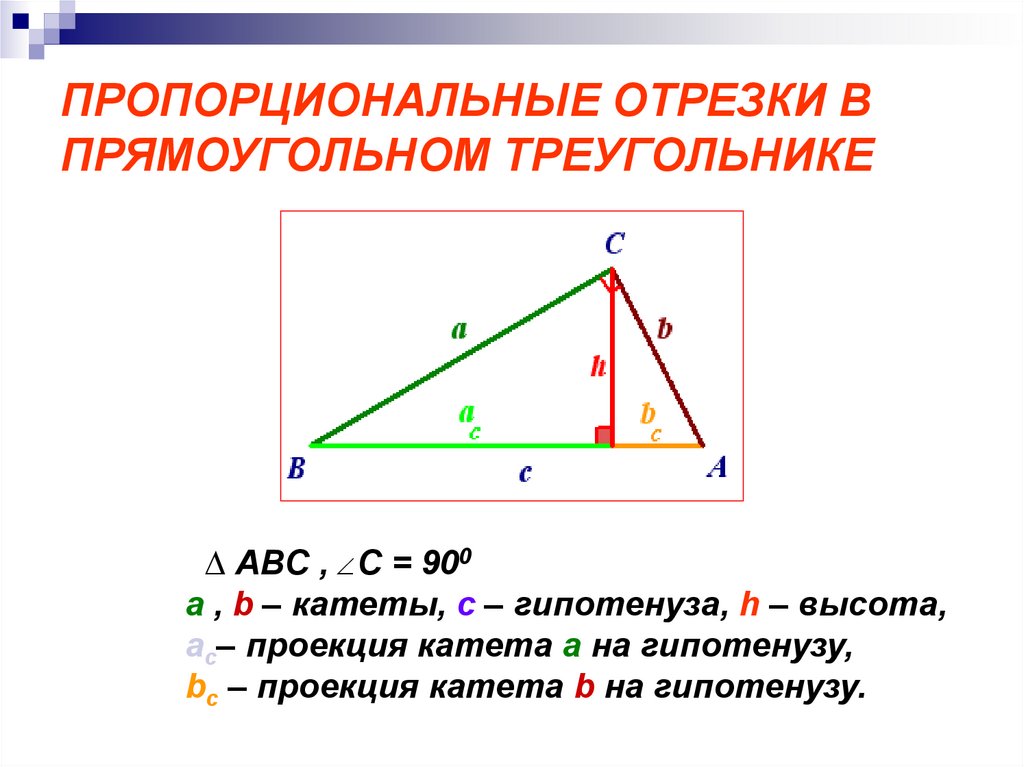
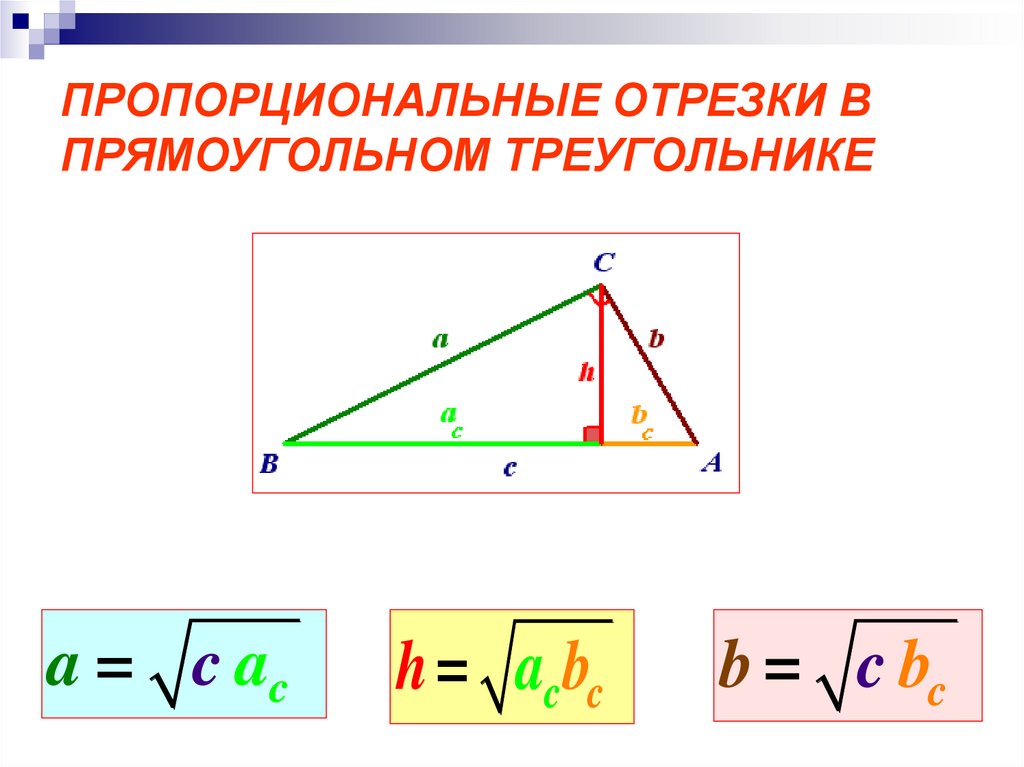
4. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
∆ ABC , C = 900a , b – катеты, с – гипотенуза, h – высота,
aс– проекция катета a на гипотенузу,
bс – проекция катета b на гипотенузу.
5. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
a = c ach = acbc
b = c bc
6. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
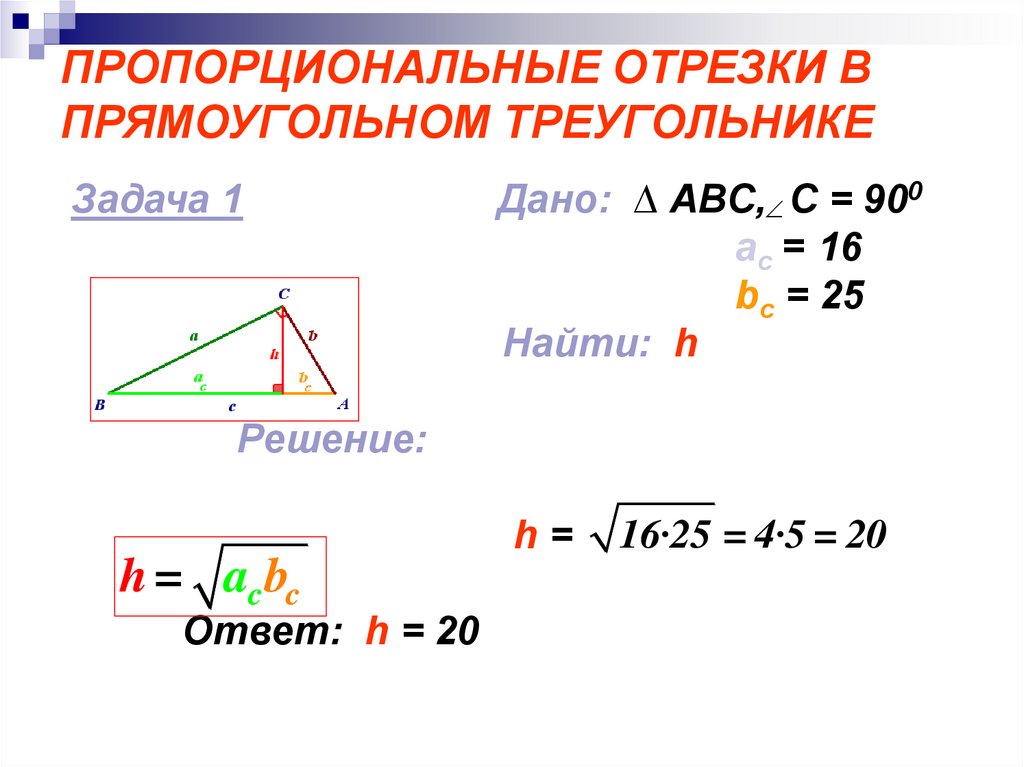
Задача 1Дано: ∆ ABC, C = 900
aс = 16
bс = 25
Найти: h
Решение:
h=
h = ac bc
Ответ: h = 20
16·25 = 4·5 = 20
7. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
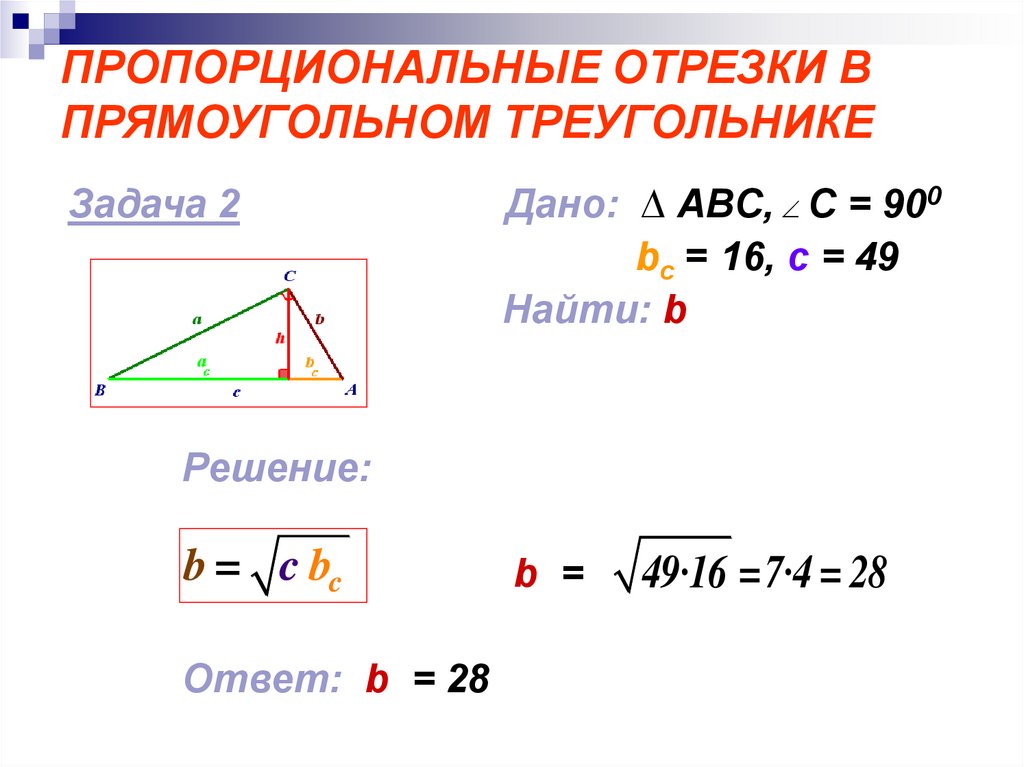
Задача 2Дано: ∆ ABC, C = 900
bс = 16, c = 49
Найти: b
Решение:
b = c bc
Ответ: b = 28
b =
49·16 =7·4 = 28
8. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
Задача 3Дано: ∆ ABC, C = 900
aс = 25
c = 49
Найти: а
Решение:
a = c ac
a=
Ответ: a = 35
49·25 =7·5 = 35
9.
Задача 4 . В треугольнике, стороны которого равны 15, 20 и 25, проведена высотак его большей стороне. Найдите отрезки, на которые высота делит эту сторону
В
15
20
?
А
Дано : АВС , АВ 15, ВС 20,
АС 25 ВН АС ,
Найти : АН и СН
С
Н
25
Заметим : АС 2 АВ 2 ВС 2
АВ 2 АН АС
252 152 202 225 400 625
625 625
АВ 2 152 225
АН
9
АС
25
25
НС 25 9 16
Вывод : В 900
10.
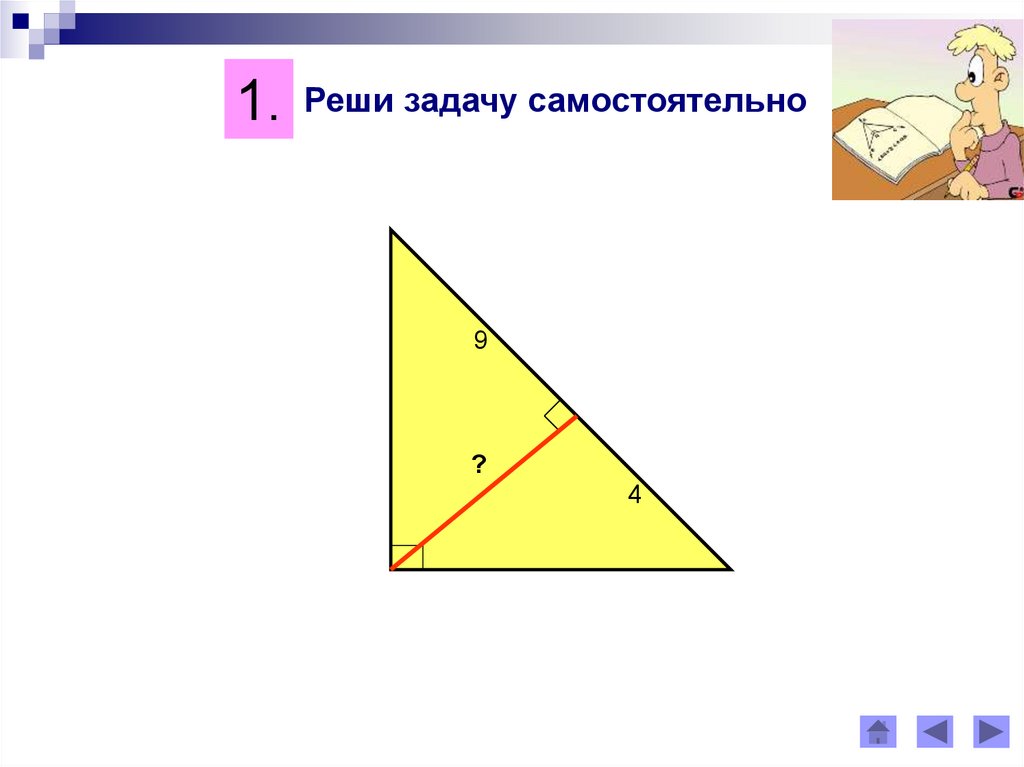
1. Реши задачу самостоятельно9
?
4
11.
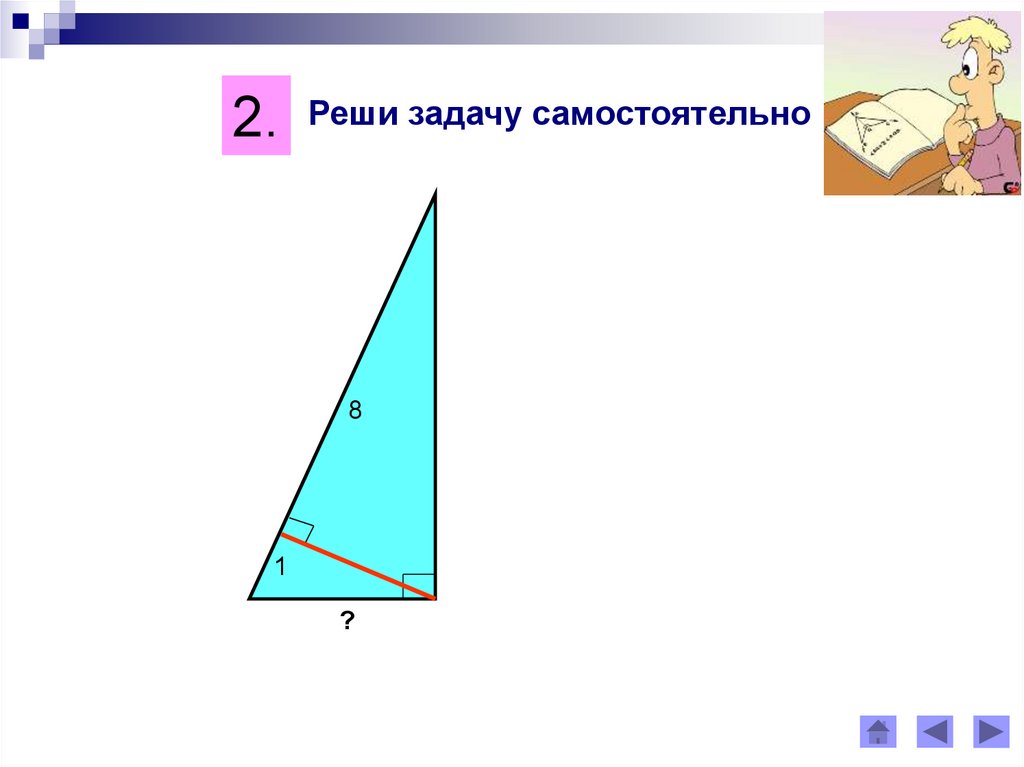
2. Реши задачу самостоятельно8
1
?
12.
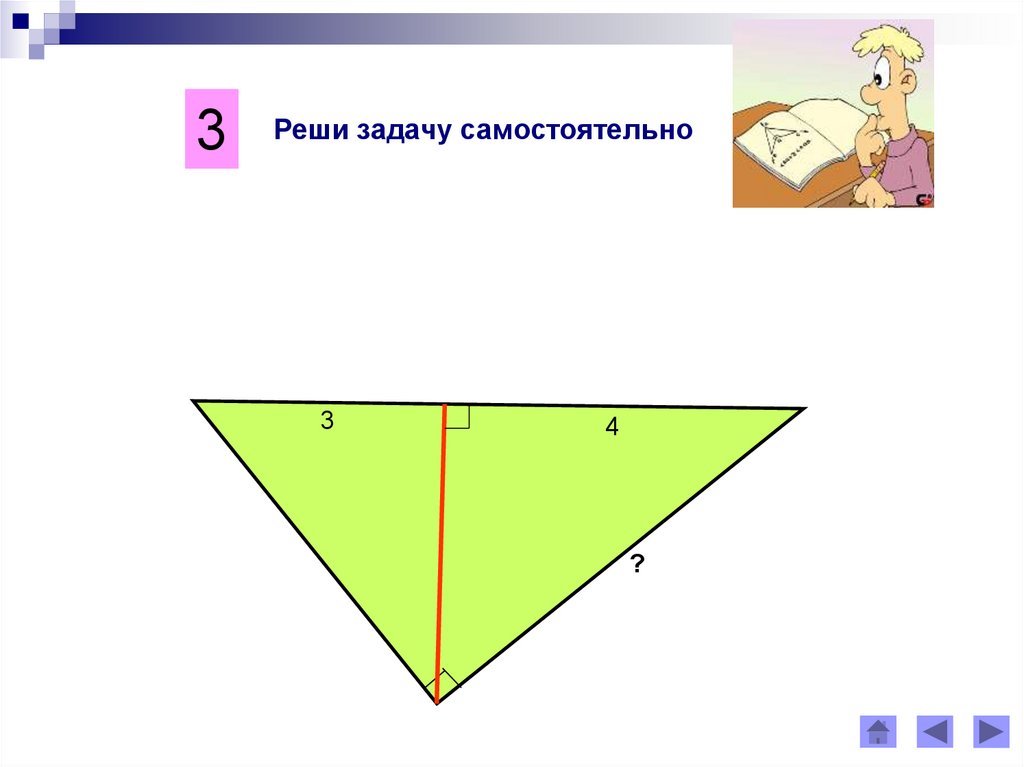
3Реши задачу самостоятельно
3
4
?
13. Домашняя работа
Геометрия 8 классСамостоятельная работа по теме «Пропорциональные отрезки в прямоугольном треугольнике»
Вариант 1
1. В прямоугольном треугольнике ас 6 см, bc 2 cм
Найдите h, c, a, b
2. В прямоугольном треугольнике АBC ( С 90 ) проведена высота CH, AH =16 cм, BH = 25
cм. Найдите:
а) CH, AB, BC, AC
3. Высота, проведенная из вершины прямого угла прямоугольного треугольника равна 6 см и
делит гипотенузу на отрезки, один из которых больше другого на 5 см. Найдите стороны
треугольника.



 mathematics
mathematics








