Similar presentations:
Геометрия дорог. Часть 2
1.
Геометрия дорогЧасть 2
Выполнила студентка 4 курса
Михайлова Оксана
2.
План вебинараВспомним, что такое параллельные прямые
Вспомним признаки параллельности прямых
Рассмотрим, что такое обратная теорема
Сформулируем теоремы об углах, образованных двумя
параллельными прямыми и секущей
● Решим задачу по данной теме
3.
Геометрия дорог4.
Взаимное расположение двух прямыхКак две прямые, лежащие в одной плоскости, могут располагаться
по отношению друг к другу?
Пересекающиеся прямые
Параллельные прямые
a
b
a
b
5.
Параллельные прямыеОпределение:
Две прямые на плоскости
называются
параллельными,
если они не пересекаются.
a
b
a ∥ b
6.
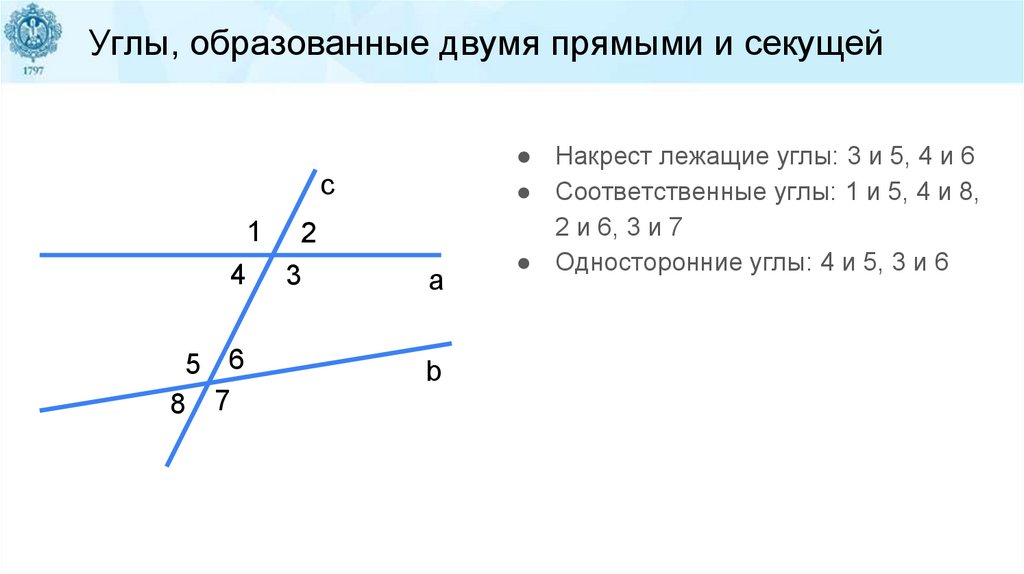
Углы, образованные двумя прямыми и секущейc
1
4
5 6
8 7
2
3
a
b
● Накрест лежащие углы: 3 и 5, 4 и 6
● Соответственные углы: 1 и 5, 4 и 8,
2 и 6, 3 и 7
● Односторонние углы: 4 и 5, 3 и 6
7.
Признаки параллельности двух прямых● Если при пересечении двух прямых секущей накрест лежащие
углы равны, то прямые параллельны.
● Если при пересечении двух прямых секущей соответственные
углы равны, то прямые параллельны.
● Если при пересечении двух прямых секущей сумма
односторонних углов равна 180°, то прямые параллельны.
8.
Евклидова геометрия● Геометрия Евклида
● «Начала» (3 век до н.э.)
● Аксиома параллельности Евклида: «И если прямая, падающая на
две прямые, образует внутренние и по одну сторону углы,
меньшие двух прямых, то продолженные неограниченно эти
прямые встретятся с той стороны, где углы меньше двух
прямых».
9.
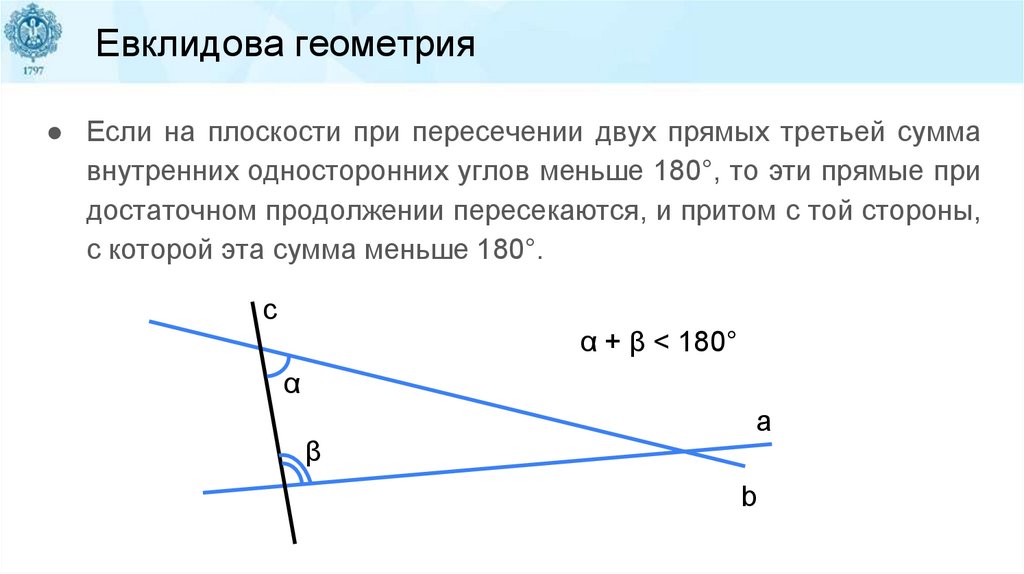
Евклидова геометрия● Если на плоскости при пересечении двух прямых третьей сумма
внутренних односторонних углов меньше 180°, то эти прямые при
достаточном продолжении пересекаются, и притом с той стороны,
с которой эта сумма меньше 180°.
c
α + β < 180°
α
β
a
b
10.
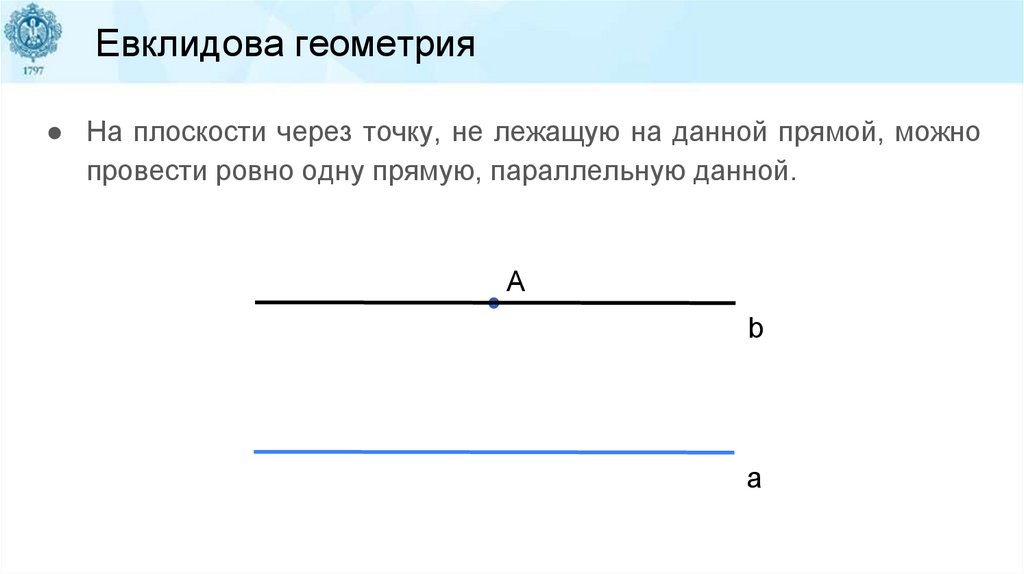
Евклидова геометрия● На плоскости через точку, не лежащую на данной прямой, можно
провести ровно одну прямую, параллельную данной.
A
b
a
11.
Неевклидова геометрия● Аксиома параллельности Лобачевского – это отрицание аксиомы
параллельности Евклида.
● Через точку, не лежащую на данной прямой, проходят по крайней
мере две прямые, лежащие с данной прямой в одной плоскости и
не пересекающие её.
A
c
b
a
12.
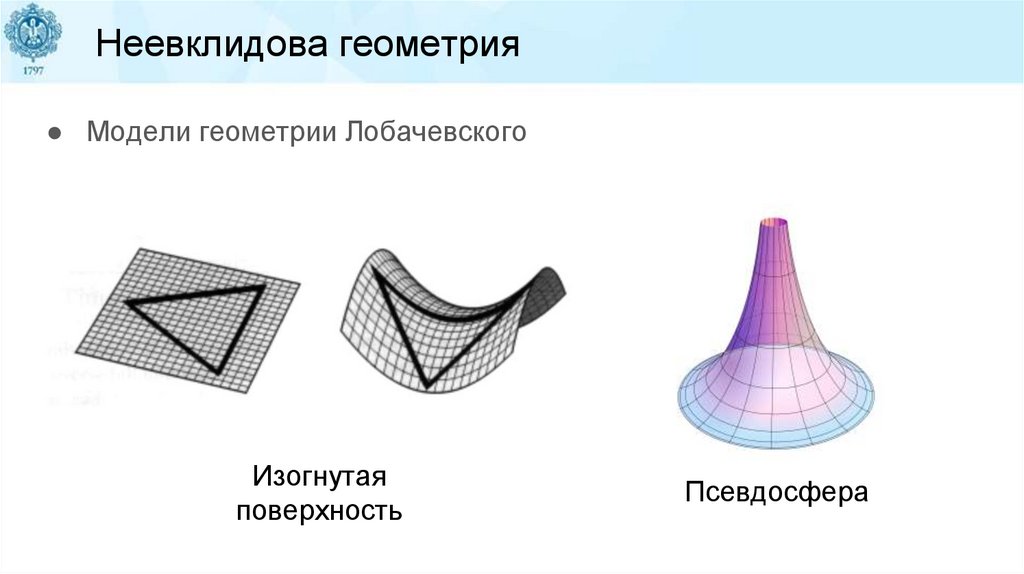
Неевклидова геометрия● Модели геометрии Лобачевского
Изогнутая
поверхность
Псевдосфера
13.
Евклидова геометрия● Две прямые на плоскости называются параллельными, если они
не пересекаются.
a
b
14.
Признаки параллельности двух прямых● Если при пересечении двух прямых секущей накрест лежащие
углы равны, то прямые параллельны.
● Если при пересечении двух прямых секущей соответственные
углы равны, то прямые параллельны.
● Если при пересечении двух прямых секущей сумма
односторонних углов равна 180°, то прямые параллельны.
15.
ТеоремаТеорема
Условие
Заключение
При
Прямые
пересечении
параллельны
двух
прямых секущей накрест
лежащие углы равны
Прямые
параллельны
При
пересечении
двух
прямых секущей накрест
лежащие углы равны
16.
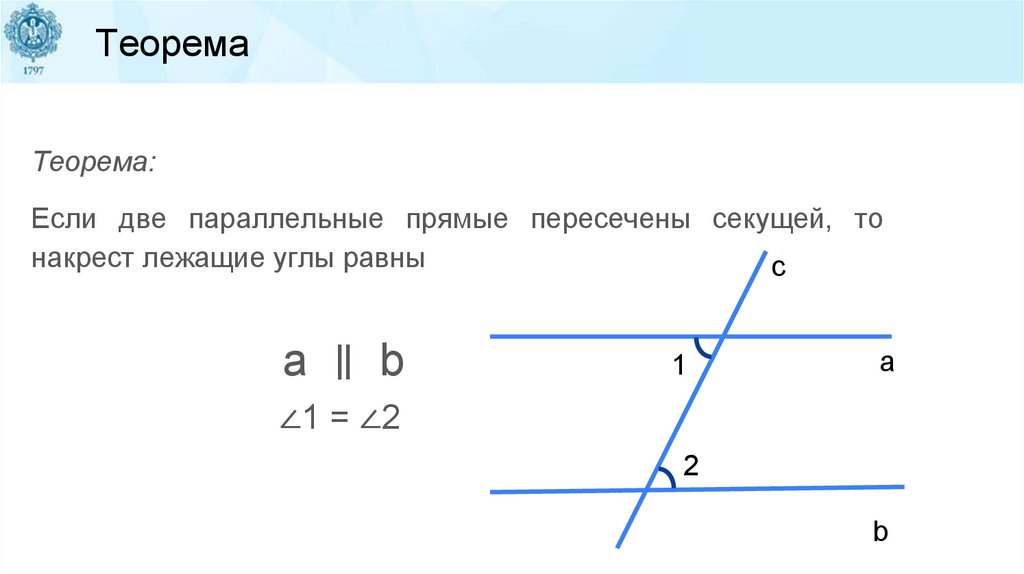
ТеоремаТеорема:
Если две параллельные прямые пересечены секущей, то
накрест лежащие углы равны
c
a ∥ b
1
a
∠1 = ∠2
2
b
17.
ТеоремаТеорема
Условие
Заключение
При пересечении
Прямые параллельны
двух прямых
секущей соответственные
углы равны
Прямые параллельны
При пересечении двух прямых
секущей соответственные
углы равны
18.
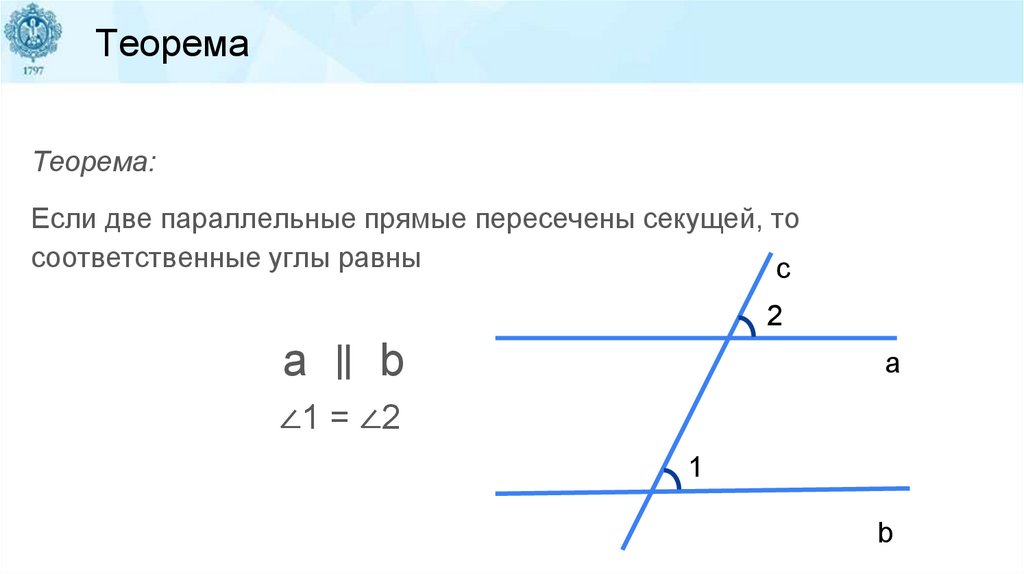
ТеоремаТеорема:
Если две параллельные прямые пересечены секущей, то
соответственные углы равны
c
2
a ∥ b
a
∠1 = ∠2
1
b
19.
ТеоремаТеорема
Условие
Заключение
Прямые
параллельны
При
пересечении
двух
прямых секущей сумма
односторонних углов
равна 180°
Прямые
параллельны
При пересечении
двух
прямых секущей сумма
односторонних углов
равна 180°
20.
ТеоремаТеорема:
Если две параллельные прямые пересечены секущей, то
сумма односторонних углов равна 180°
c
a ∥ b
1
a
∠1 + ∠2 = 180°
2
b
21.
ЗадачаДве дороги со встречным движением проложены параллельно друг
другу, чтобы избежать аварии. Дорожным строителям была
поставлена задача проложить третью дорогу под углом 60° к одной
из данных дорог. С учетом подземных коммуникаций эта дорога
должна быть проложена под углом не более 70° ко второй данной
дороге. Возможно ли проложить такую дорогу?
22.
Решение задачиa ∥ b
∠EAC = 60°
∠EAC = ∠EBD (соответственные при
a ∥ b и секущей c)
∠EBD = 60°≤ 70°
E
C
D
c
a
A
B
b
Ответ: да, такую дорогу возможно проложить
23.
Итоги вебинараНа вебинаре мы:
● Вспомнили определение и признаки параллельности двух
прямых
● Познакомились с обратной теоремой
● Рассмотрели теоремы об углах, образованных двумя
параллельными прямыми и секущей
● Закрепили теоретический материал с помощью задачи

















 mathematics
mathematics