Similar presentations:
Алгебра и начала анализа. 10 класс
1.
ФКОУ СОШ ГУФСИН России по Свердловской областиРАЗДЕЛ «ЛОГАРИФМИЧЕСКАЯ
ФУНКЦИЯ» (СПРАВОЧНЫЙ МАТЕРИАЛ)
АЛГЕБРА И НАЧАЛА АНАЛИЗА 10 КЛАСС
УЧИТЕЛЬ МАТЕМАТИКИ:
ФАЛАХУТДИНОВА Р.Н.
2.
1) ЛОГАРИФМЫОпределение. Логарифмом по основанию а от аргумента x
называют степень, в которую нужно возвести а, чтобы
получить х.
logax = b
Где:
а – основание логарифма;
х – аргумент (число или выражение под знаком логарифма);
b – значение логарифма.
Например:
log28 = 3
(логарифм по основанию 2 от числа 8 равен 3, поскольку 23 = 8 )
3.
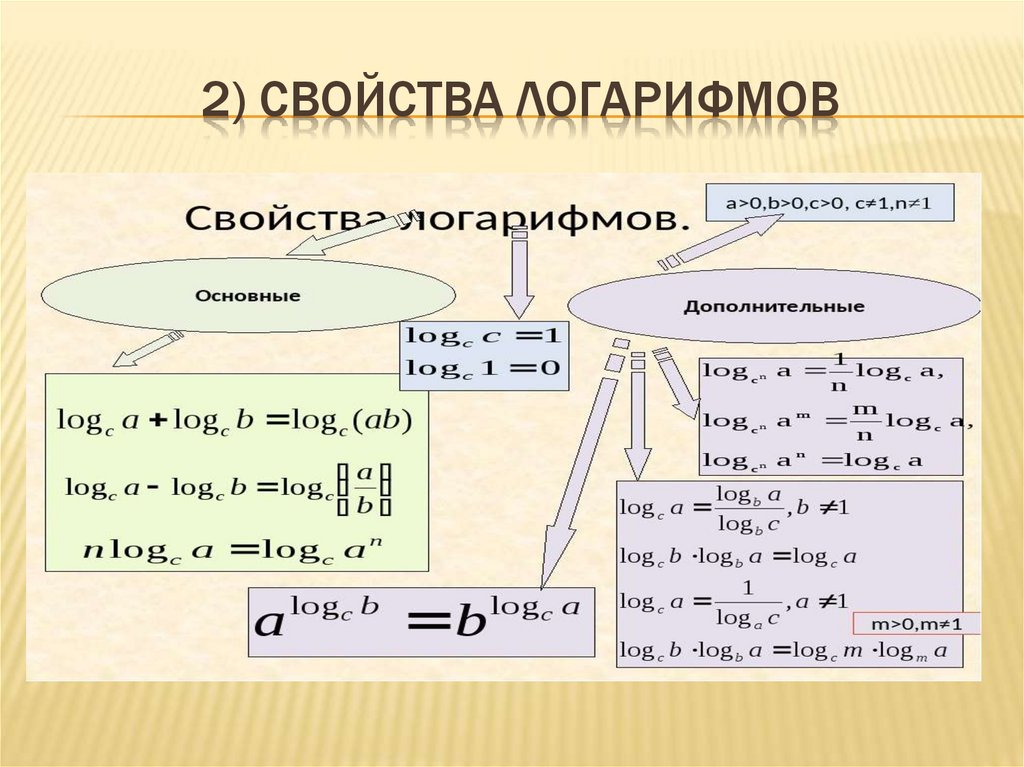
2) СВОЙСТВА ЛОГАРИФМОВ4.
5.
3) ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕЛОГАРИФМЫ
6.
ПРИМЕРЫ7.
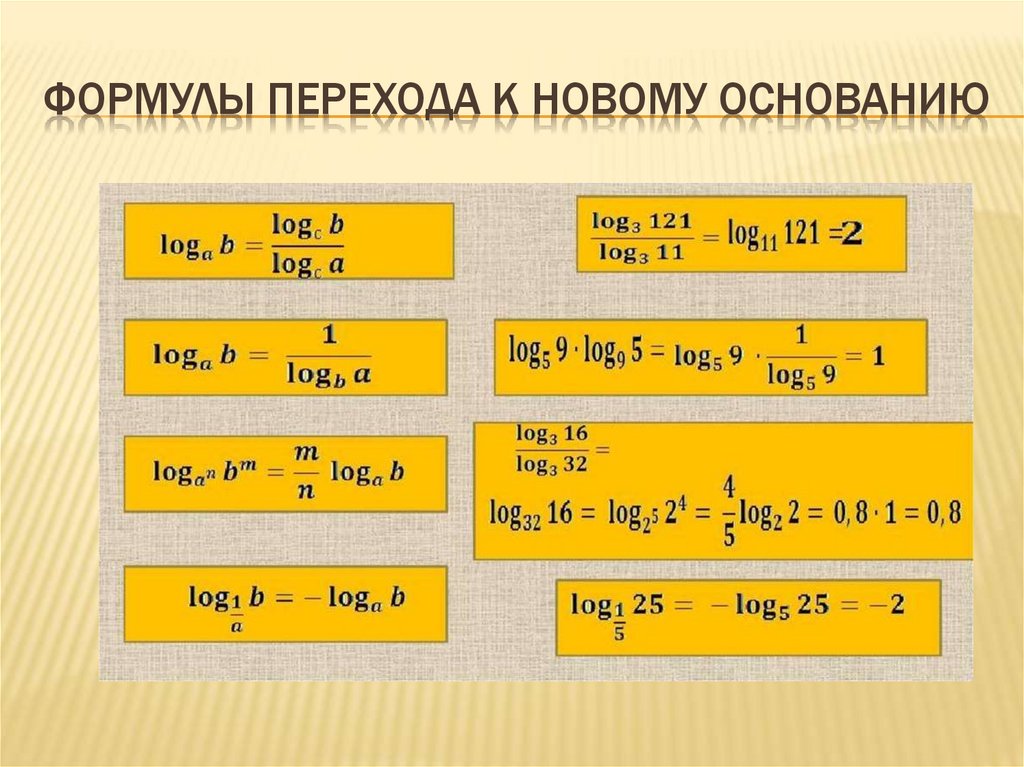
ФОРМУЛЫ ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ8.
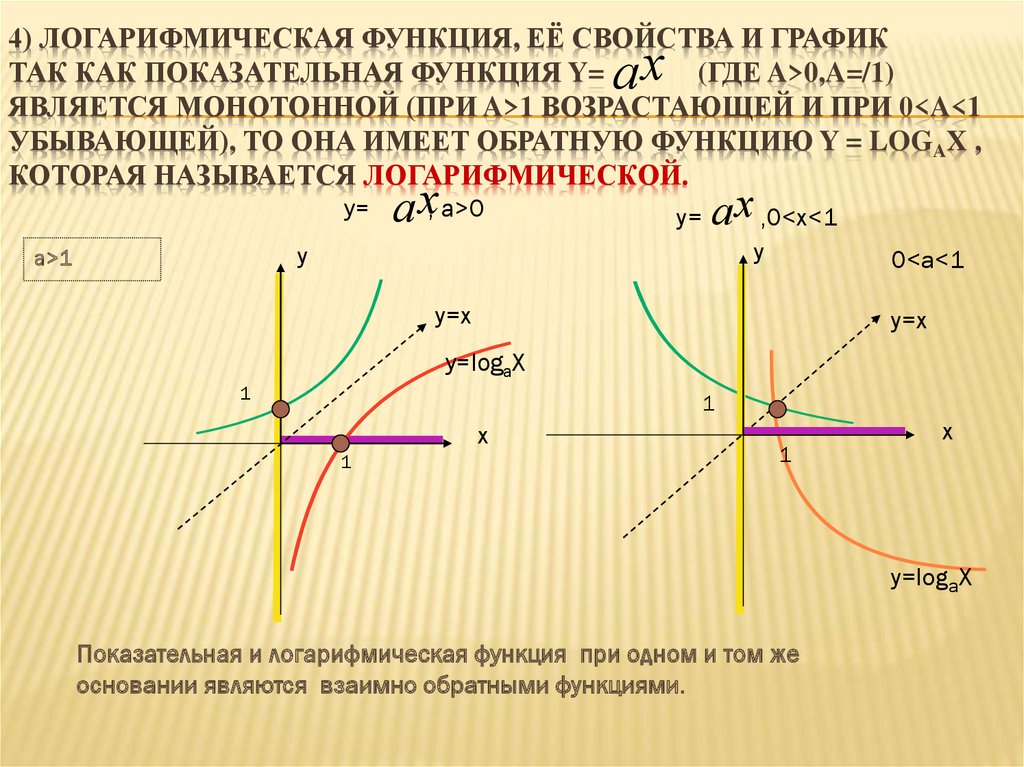
4) ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЁ СВОЙСТВА И ГРАФИКТАК КАК ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ Y=
(ГДЕ A>0,A=/1)
ЯВЛЯЕТСЯ МОНОТОННОЙ (ПРИ A>1 ВОЗРАСТАЮЩЕЙ И ПРИ 0<A<1
УБЫВАЮЩЕЙ), ТО ОНА ИМЕЕТ ОБРАТНУЮ ФУНКЦИЮ Y = LOGAX ,
КОТОРАЯ НАЗЫВАЕТСЯ ЛОГАРИФМИЧЕСКОЙ.
ах
y=
а х, a>0
y=
а х ,0<x<1
y
y
a>1
0<a<1
y=x
y=x
y=logaX
1
1
x
1
1
x
y=logaX
Показательная и логарифмическая функция при одном и том же
основании являются взаимно обратными функциями.
9.
СВОЙСТВА ФУНКЦИИ.1.Область определения- Множество всех положительных чисел(x>0)
2.Множество значений- Множество всех действительных чисел
3.График функции проходит через точку(1;0)
4.На промежутке x>0 функция является
Возрастающей
убывающей
5.Функция принимает положительные значения(y>0)
Х>1
6.Функция принимает отрицательные значения(y<0)
0<x<1
x>1
y
y
y log a x
1
0
0<x<1
y log a x
1
0
1
a 1
1
0 a 1
10.
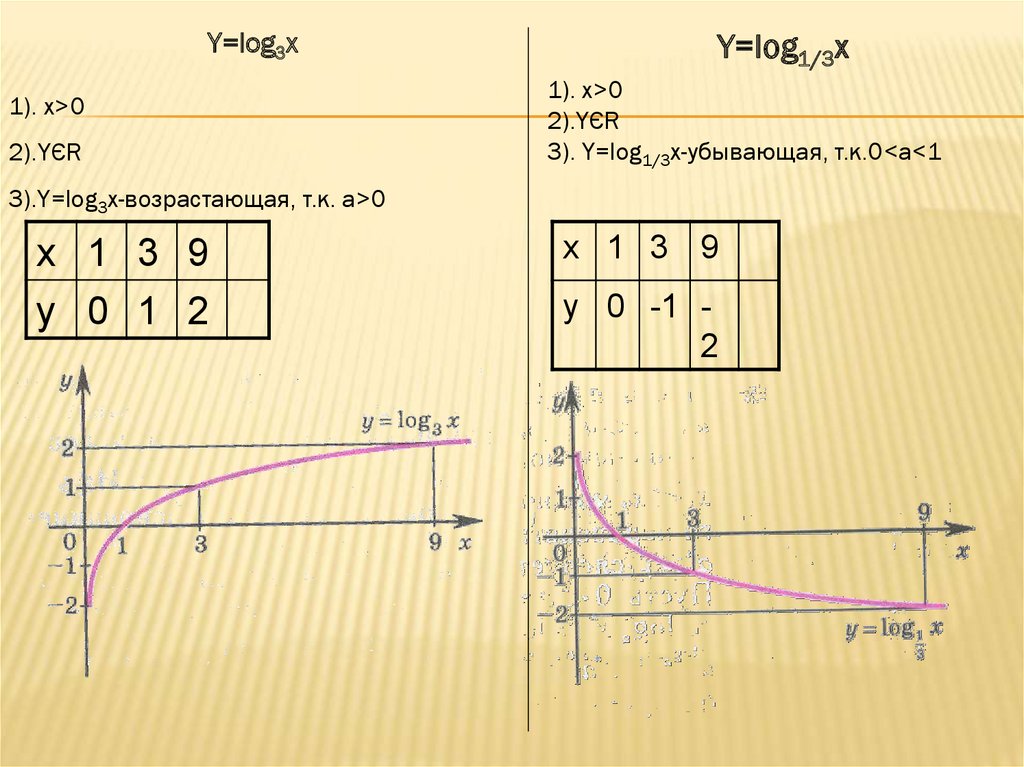
Y=log3x1). x>0
2).YЄR
Y=log1/3x
1). x>0
2).YЄR
3). Y=log1/3x-убывающая, т.к.0<a<1
3).Y=log3x-возрастающая, т.к. а>0
x 1 3 9
y 0 1 2
x 1 3 9
y 0 -1 2
11.
5)ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ12.
МЕТОДЫ РЕШЕНИЯ ЛОГАРИФМИЧЕСКИХУРАВНЕНИЙ
1.Простейшее логарифмическое уравнение
2. Логарифмическое уравнение, решаемое потенцированием
3. Логарифмическое уравнение, решаемое введением новой
переменной
4. Логарифмическое уравнение, решаемое логарифмированием
5. Графическое решение
6.
13.
Уравнение:log 3 (5 x 1) 2
log 2 х 2 log x 2 1
log
3
Метод решения
по определению логарифма
переход к другому основанию
( x 2) log 5 x 2 log 3 ( x 2) разложение на множители
log 3 (5 x 3) log 3 (7 x 5) потенцирование
log 22 x 3 log 2 x 4
введение новой переменной
log 3 x 9 log 27 8 3 log 3 4 переход к другому основанию
log 2 ( x 2) log 2 ( x 3) 1
lg3 x 5 lg x
x
log 1 x 2 x
0,0001
использование свойств
логарифма
логарифмирование
графический
2
13
14.
15.
6) ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВААлгоритм решения:
1. Найти ООФ
2. Решить логарифмическое неравенство, применяя :
- свойства логарифмов( сужать ООФ нельзя, т.е
нельзя логарифмировать );
- монотонность логарифмической функции(
возрастание и убывания функции).
3. Выбрать общее решение
ООФ
решение неравенства
16.
ПРИМЕРЫ:17.
ИЗПОЛЬЗУЕМЫЕ РЕСУРСЫ1) https://ieducations.ru/wpcontent/uploads/7/7/c/77cd22a1b1c35908e
26f1033e8cd9d31.jpeg
2) https://my.1sept.ru/
3) УМК Ш.А.Алимов, Ю.М. Колягин Алгебра и
начала анализа.Москва «Просвещение 2020»













 mathematics
mathematics