Similar presentations:
История создания страны формул
1. История создания страны формул:
ДиофантАлександрийский
(III век н. э.) —
древнегреческий
математик.
Еще в глубокой древности
было замечено, что некоторые
многочлены можно умножать
быстрее, чем все остальные.
Так, древнегреческими
математиками еще до нашей
эры (более 2000 лет назад)
геометрическим способом
были выведены некоторые
формулы, которые получили
название формулы
сокращенного умножения.
2. Формулы сокращенного умножения
квадрат суммыи
квадрат разности
двух выражений
3. ЭПИГРАФ К УРОКУ:
«У МАТЕМАТИКОВ СУЩЕСТВУЕТСВОЙ ЯЗЫК –
ЭТО
ФОРМУЛЫ»
С. В. Ковалевская
(1850-1891)
4. Устная работа
• Найти квадраты выраженийy; 4; -2/7; 3m; 8xy; 5a2b.
• Найти произведение одночленов
6x и 9h.
Чему равно их удвоенное произведение?
• Прочитать выражение:
a) m + n
б) (m+n)2
в) m2+n2
г) 2mn
д) (m-n)2
е) m2 - n2
• Выполнить умножение многочленов (c-5)(r+2).
5. №1
Результат умножения1) (m + n) (m + n) =
=
2) (c + d) (c + d) =
=
3) (p + q) (p + q) =
=
4) (k + 3) (k + 3) =
=
5) ( 5 + m)( 5 + m) =
=
6. №1
Результат умножения1) (m + n) (m + n) =
= m2 + 2 m n + n 2
2) (c + d) (c + d) =
= c2 + 2 c d + d 2
3) (p + q) (p + q) =
= p2 + 2qp + q2
4) (k + 3) (k + 3) =
= k2 + 6 k + 9
5) ( 5 + m)( 5 + m) =
= n2 + 10 n + 25
7. №1
1) (m + n) (m + n) =(m + n)2
= m2 + 2 m n + n 2
2) (c + d) (c + d) =
(c + d) 2
= c2 + 2 c d + d 2
3) (p + q) (p + q) =
(p + q)2
= p2 + 2qp + q2
4) (k + 3) (k + 3) =
(k + 3)2
= k2 + 6 k + 9
5) ( 5 + m)( 5 + m) =
( 5 + m)2
= n2 + 10 n + 25
8. ОТКРЫТИЕ № 1
ФОРМУЛАКВАДРАТ СУММЫ ДВУХ
ВЫРАЖЕНИЙ:
(а +
2
b) =
2
а
+ 2аb +
2
b
9. ПРИМЕНЕНИЕ ФОРМУЛЫ КВАДРАТА СУММЫ (а + b)2 = а2 + 2аb + b2
Вместо a и b в эту формулу можно подставить любыевыражения
ШИФРОГРАММЫ:
10. №2
Результат умножения1) (m - n) (m - n) =
=
2) (c - d) (c - d) =
=
3) (p - q) (p - q) =
=
4) (k - 3) (k - 3) =
=
5) ( 5 - m)( 5 - m) =
=
11. №2
Результат умножения1) (m - n) (m - n) =
= m2 - 2 m n + n 2
2) (c - d) (c - d) =
= c2 - 2 c d + d2
3) (p - q) (p - q) =
= p2 - 2qp + q2
4) (k - 3) (k - 3) =
= k2 - 6 k + 9
5) ( 5 - m)( 5 - m) =
= n2 - 10 n + 25
12. №2
1) (m - n) (m - n) =(m - n)2
= m2 - 2 m n + n 2
2) (c - d) (c - d) =
(c - d) 2
= c2 - 2 c d + d2
3) (p - q) (p - q) =
(p - q)2
= p2 - 2qp + q2
4) (k - 3) (k - 3) =
(k - 3)2
= k2 - 6 k + 9
5) ( 5 - m)( 5 - m) =
( 5 - m)2
= n2 - 10 n + 25
13. ОТКРЫТИЕ № 2
ФОРМУЛАКВАДРАТ РАЗНОСТИ ДВУХ
ВЫРАЖЕНИЙ:
(а -
2
b) =
2
а
- 2аb +
2
b
14. ПРИМЕНЕНИЕ ФОРМУЛЫ КВАДРАТА РАЗНОСТИ (а - b)2 = а2 - 2аb + b2
ШИФРОГРАММЫ:15. Найдите ошибки:
НАЙДИТЕ ОШИБКИ:2
у)
2
2
у
(b = b – 2bу +
2
2
(6 + с) = 36 +- 12с + с
2
2
(р - 10) = р - 20р + 100
2
2
(2а + 1) = 4а + 42а + 1
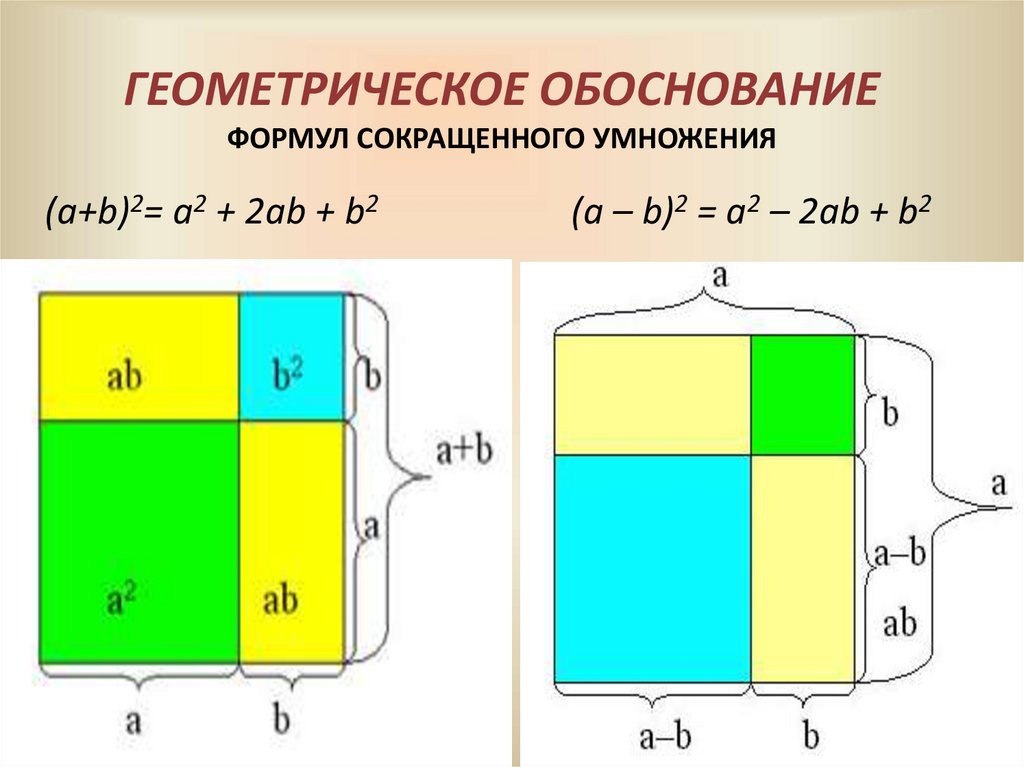
16. Геометрическое обоснование формул сокращенного умножения
ГЕОМЕТРИЧЕСКОЕ ОБОСНОВАНИЕФОРМУЛ СОКРАЩЕННОГО УМНОЖЕНИЯ
(a+b)2= a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
17.
Представить в виде многочлена:1) f d
f 2 fd d
2) m 1
m 2m 1
3) 3k 4
9k 24k 16
2
2
2
2
2
2
4) 2 x 7 y
2
4 x 28 xy 49 y
6) b d
7) 5 p 4q
5) c k
2 2
3 2
2
3
4 2
2
4
c 2ck k
2
2
4
b 2b d d
4
2
3
2
6
25 p 40 p q 16q
6
3
4
8
18.
Представить в виде многочлена:1) s z
s 2 sz z
2) m 1
m 2m 1
3) 4 3k
16 24k 9k
4) 5 x 2 y
25 x 20 xy 4 y
2
2
2
2
2
6) t c
7) 3m 4n
2
5) k p
2
7 2
4
6
3 2
2
2
2
2
k 2k p p
4
2
2
2
t 2t c c
8
4 7
14
9m 24m n 16n
12
6
3
6
19.
Мало иметьхороший ум,
главное –
уметь его
применять
Рене Декарт — (1596-1650)
— французский философ,
математик, физик и
физиолог



















 mathematics
mathematics








