Формулы сокращенного умножения. Квадрат суммы и квадрат разности двух выражений

1.

Формулы сокращенного
умножения
Квадрат суммы и
квадрат разности
двух выражений
Учитель математики МБОУ г. Мценска
«Средняя школа №7»
Курсикова И.В.

2.

Еще в глубокой древности было
замечено, что некоторые многочлены
можно умножать быстрее, чем все
остальные. Так, древнегреческими
математиками еще до нашей эры (более
2000 лет назад) геометрическим
способом были выведены некоторые
формулы, которые получили название
формулы сокращенного умножения.
Диофант Александрийский (III век н. э.)
— древнегреческий математик.

3.

Эпиграф к уроку
«У математиков есть свой
язык - формулы»
С.В. Ковалевская

4.

Устный счет
1)Найдите квадраты выражений: a; -5; 4m; 3х.
2) Найдите произведение 5х и 3у.
3) Найдите удвоенное произведение
выражений: 3х и 6у.
4)Прочитайте выражения: х+у; (х+у)²; а-в; (а-в)²;
х²−y², 2mn, m2+n2 .
5) Как умножить многочлен на многочлен?
6)Выполните умножение выражений (х+2)(х-4).
7)Выполните умножение выражений (х+3)(х-3)

5.

Цели урока:
1. Вывести формулы сокращённого умножения:
квадрат суммы и квадрат разности
2. Закрепить умения и навыки применения
формул сокращённого умножения на
решении математических задач.

6.

Исследование 1
Результат умножения
(m + n) (m + n) =
=
(b + c) (b + c) =
=
(p + q) (p + q) =
=
(k + 3) (k + 3) =
=
( 4 + d)( 4 + d)=
=

7.

Исследование 1
Результат умножения
(m + n) (m + n) =
= m 2 + 2 m n + n2
(b + c) (b + c) =
= b2 + 2 bc + c2
(p + q) (p + q) =
= p2 + 2 pq + q2
(k + 3) (k + 3) =
= k2 + 6k + 9
( 4 + d)( 4 + d)=
= 16 + 8d + d2

8.

Исследование 1
Результат умножения
(m + n) (m + n) =
(m + n)2
= m 2 + 2 m n + n2
(b + c) (b + c) =
(b + c)2
= b2 + 2 bc + c2
(p + q) (p + q) =
(p + q)2
= p2 + 2 pq + q2
(k + 3) (k + 3) =
(k + 3)2
= k2 + 6k + 9
( 4 + d)( 4 + d)=
(4 + d)2
= 16 + 8d + d2

9.

Исследование 2
Результат умножения
(m - n) (m-n) =
=
(b - c) (b - c) =
=
(p - q) (p - q) =
=
(k - 3) (k - 3) =
=
( 4 - d)( 4 - d)=
=

10.

Исследование 2
Результат умножения
(m - n) (m-n) =
= m 2 - 2 m n + n2
(b - c) (b - c) =
= b2 - 2 bc + c2
(p - q) (p - q) =
= p2 - 2 pq + q2
(k - 3) (k - 3) =
= k2 - 6k + 9
( 4 - d)( 4 - d)=
= 16 - 8d + d2

11.

Исследование 2
Результат умножения
(m - n) (m-n) =
(m - n)2
= m 2 - 2 m n + n2
(b - c) (b - c) =
(b - c)2
= b2 - 2 bc + c2
(p - q) (p - q) =
(p - q)2
= p2 - 2 pq + q2
(k - 3) (k - 3) =
(k - 3)2
= k2 - 6k + 9
( 4 - d)( 4 - d)=
(4 - d)2
= 16 - 8d + d2

12.

Формулы сокращенного умножения
КВАДРАТ СУММЫ ДВУХ ВЫРАЖЕНИЙ:
(а + b)2 = а2 + 2аb + b2
КВАДРАТ РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ:
(а - b)2 = а2 - 2аb + b2

13.

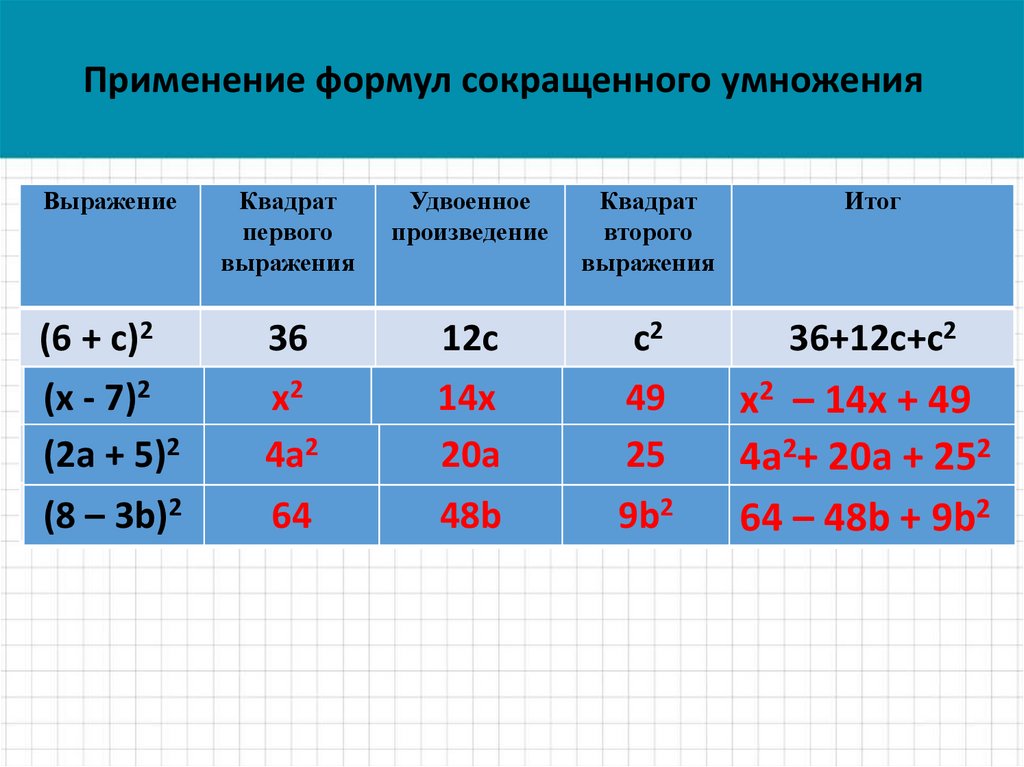
Применение формул сокращенного умножения
Выражение
Квадрат
первого
выражения
Удвоенное
произведение
Квадрат
второго
выражения
Итог
(6 + с)2
(х - 7)22
(2а + 5)22
(8 – 3b)22
36
x2
4a2
12с
14x
20a
с2
49
25
36+12с+с2
64
48b
9b2
x2 – 14x + 49
4a2+ 20a + 252
64 – 48b + 9b2

14.

Применение формул сокращенного умножения
НАЙДИТЕ ОШИБКИ:
2
2
(x - у) = x – 2 x у + у2
(9 + с)2 = 81 –189 с + с2
(k- 10)2 =k2 – 20k + 100
10
(2а + 3)2 = 4 а2 + 12
6 аа + 9

15.

Применение формул сокращенного умножения
ЗАПОЛНИТЕ ПРОПУСКИ …
(х … у)2 = х2 - 2х + …
(... + ...)2 = 9х2 ... ... + 25у2
(... ... ...)2 = ... - 24ху ... 36х2
(х - ... )2 = ... ... 20х ... ...
(… … …)2 = 25a2 + … + b2

16.

Применение формул сокращенного умножения
ЗАПОЛНИТЕ ПРОПУСКИ …
(х - у)2 = х2 - 2х + у2
(3а + 5у)2 = 9а2 + 30ау + 25у2
(2у - 6х)2 = 4у2 - 24ху + 36х2
(х - 10 )2 = х2 - 20х + 100
(5а + b)2 = 25a2 + 10ab + b2

17.

Геометрическое обоснование формулы
сокращенного умножения (a + b) =a2 + 2ab + b2

18.

Работа с учебником
№ 800 (д,е,ж,з)
№ 808

19.

Итог урока
- С какими формулами мы познакомились сегодня на
уроке?
- Почему эти формулы называются формулами
сокращенного умножения?
- Чему равен квадрат суммы двух выражений?
- Чему равен квадрат разности двух выражений?
- Зачем нужны нам эти формулы и стоит ли их
запоминать?

20.

Домашнее задание
п.32. № 803, №814(а,б,в)
Доказать геометрический смысл формулы
(a - b)2 №801.