Вывод формулы умножения разности двух выражений на их сумму

1.

АЛГЕБРА
7 класс
«Вывод формулы
умножения разности двух
выражений на их сумму»
06.04.2020г.
1

2.

Ф о р м ул ы с о к р а щ е н н о го у м н ож е н и я
ТЕМА:
« Ум н о ж е н и е р а з н о с т и
двух выражений
на их сумму»
Цели урока:
1. Вывести формулу произведения разности
двух выражений на их сумму
2. Тренироваться в применении этой формулы
3. Научиться пользоваться ею для устных вычислений
4. Рассмотреть геометрический смысл формулы
2

3.

Ф о р м ул ы с о к р а щ е н н о го у м н ож е н и я
Математическая разминка
1 . 2П р2о ч и2 т а й2 т е 2в ы р а ж е2 н и я :
(a 5) ; a 5 ; x y ; (m n) ;
2
(a 5) ;
2
2
a 5 ;
2
2
x y ;
1
2
(m n) ;
1
4c2
2 0,25b2; ( a 2c)2
a
(3x)22 . 9 xВ2;ы(0,5
b
)
п о л н и т е д е4 й с т в16и я :
(3x)22
3p
9 x22;
(3 p)
;
1 2 2
1
2
2
(0,5b(8
) d )20,25
b ;2 ( a c)
64d
4
16
a4c2
3 . Является ли тождеством равенство:
3p2 (3 p)2 ;
(8d )2 64d 2
Важны ли скобки в подобных записях?
3

4.

Ф о р м ул ы с о к р а щ е н н о го у м н ож е н и я
Сейчас – небольшой м а т е м а т и ч е с к и й
Запишем любое двузначное число, например
фокус !
69 71 4899
69 71 4899
37 43
52 48
201 199
399 401
Еще несколько примеров :
здесь и трехзначные числа.
Все эти произведения можно
вычислить устно.
Сейчас я это проделаю на ваших
глазах.
37 43
52 48
201 199
399 401
Для этого познакомимся
еще с одной формулой из группы
«Формулы сокращенного умножения»
4

5.

Ф о р м ул ы с о к р а щ е н н о го у м н ож е н и я
В ы п о л н и м у м н ож е н и е р а з н о с т и д ву х в ы р а ж е н и й
2 и й2:
н а с(aу м
а ж еbн
bм) у (aэ т иb)х жa 2е вabы рab
a b2
(a b) (a b) a ab ab b a b
2
2
a
b
a
b
a
b
И т а к , п о л у ч и л и :
2
a b a b a
2
2
b
2
2
2
(1)
Произведение разности двух выражений и их суммы
равно разности квадратов этих выражений.
Тож д е с т во ( 1 ) п о з вол я е т с о к р а щ е н н о
в ы п ол н я т ь ум н оже н и е р а з н о с т и л ю б ы х
д ву х в ы р а же н и й н а и х сум м у.
5

6.

Ф о р м ул ы с о к р а ще н н о го у м н оже н и я
a b a b a b
2
2
a b a b a b
2
2
2 x2 4
( x 2) ( x примеры
2) x2 2применения
Рассмотрим
этой формулы:
2 222 x22 4
2
2
(
x
2)
(
x
2)
x
(5a 8b) (5a 8b) (5a) (8b) 25a 64b
(5a 8b) (5a 8b) (5a)2 (8b)2 25a2 64b2
6

7.

Ф о р м ул ы с о к р а щ е н н о го у м н ож е н и я
2
2
a
b
a
b
a
b
a b a b a
2
b
2
(0,7c 9d ) (9d 0,7c) (0,7c 9d ) (0,7c 9d )
2 (9d )2 0,49c2 81d 2
(0,7
c
)
(0,7c 9d ) (9d 0,7c) (0,7c 9d ) (0,7c 9d )
2 ) 81
(3m (0,7
n) (cn) 23m
) d(n) 23m
(n c3m
d2
(9
)0,49
n2 (3m)2 n2 (9m)2
(3m 2n) 2(n 3m)2 2(n 32m) 4 (n 3m)
(0,4 y ) ( y 0,4) ( y ) (0,4) y 0,16
n2 (3m)2 n2 (9m)2
(0,4 y 2 ) ( y 2 0,4) ( y 2 )2 (0,4)2 y 4 0,16
7

8.

О б р ат и т е в н и м а н и е ! В п е р еч и с л е н н ы х в ы ш е п р и м е р а х
к в а д р ат ы в ы р а же н и й с т оя т в т а к о й же
п о с л е д ов ат е л ь н о с т и , к а к и в с к о б ке с р а з н о с т ь ю .
a b a b a 2 b2
2
2
b 2)37
a 43 b
a b 1)69 a 71
3)52 48 1)69
4)201
199
А теперь вернемся
71
2)37 43
к нашему устному
5)399 401 6)603 597
3)52 48 4)201 199
счету:
5)399
2401 6)603 597
2
(70 1) (70 1) 70 1
Рассмотрим,
например,
произведение
69 71
4900 1
(70 1) (70 1) 702 12
4900 1 4899
8

9.

Ф о р м ул ы с о к р а ще н н о го у м н оже н и я
a b a b a 2 b2
2
2
a b a b a b
Попробуйте вычислить устно таким же способом остальные
произведения.
Запишите их в виде произведения разности и суммы
соответствующих чисел, и зафиксируйте ваши ответы в
тетрадях:
37x43 = 1591
399x401 = 159999
52x48 = 2496
603x597 = 359991
201x199 =39999
9

10.

Ф о р м ул ы с о к р а щ е н н о го у м н ож е н и я
И н т е р е с н ы й
ф а к т
Некоторые формулы сокращенного умножения, в том числе и
п р о и з в е д е н и е р а з н о с т и н а с у м м у,
были известны еще около 4000 лет назад: об этом
свидетельствуют найденные вавилонские клинописные тексты.
У древних греков они тоже были известны, но не в нашем
символическом виде, а в г е о м е т р и ч е с к о й ф о р м е .
Ученые древней Греции представляли величины не числами
или буквами, а отрезками прямых.
Вместо произведения ab говорилось (и рассматривался)
«прямоугольник, содержащийся между
2
2отрезками a и b»,
a
b
a
b
a
b
вместо a 2 – « к в а д р ат н а о т р е з ке a » .
Эта алгебра была названа «геометрической алгеброй».
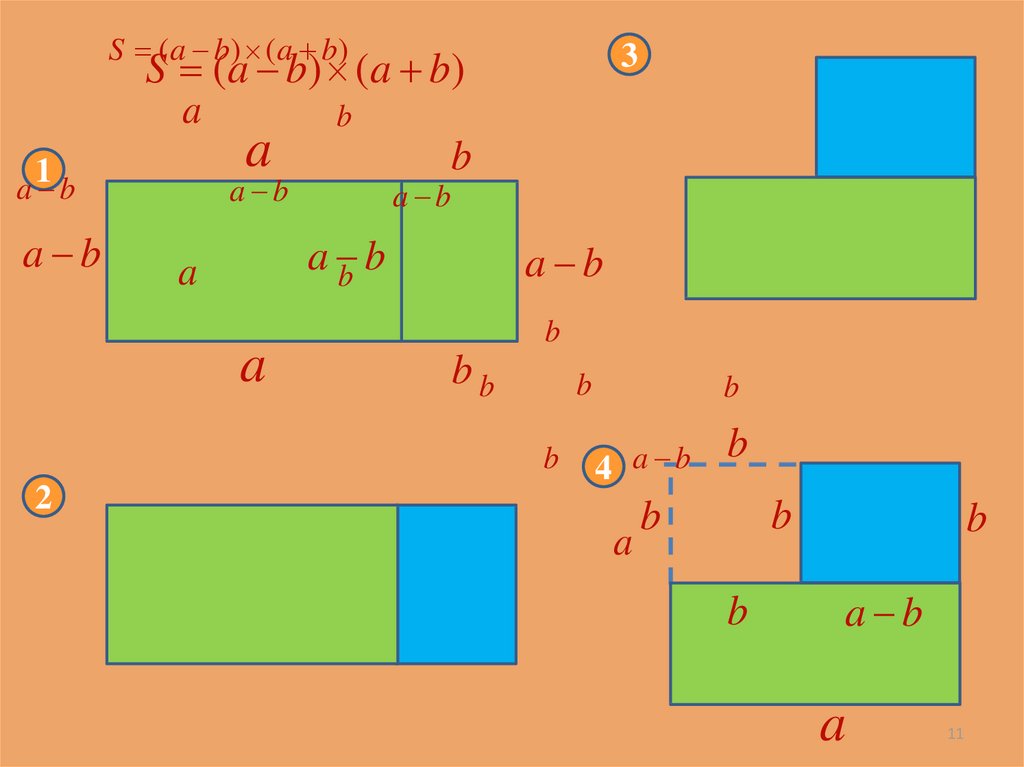
Давайте разберемся в г е о м е т р и ч е с к о м с м ы с л е
ф о р м ул ы :
a b a b a
2
b
2
10

11.

S ( a b) ( a b)
S ( a b) ( a b)
a
1
a b
a b
a
b
a b
a b
b
a b b
a
a
3
a b
b
bb
b
b
2
b
4 a b
a
b
b
b
b
b
a b
a
11

12.

Ф о р м ул ы с о к р а ще н н о го у м н оже н и я
Подведем итоги нашего урока
Что нового узнали на уроке?
Произведение разности двух
выражений и их суммы
2
2
равно
разности
квадратов
этих
a
b
a
b
a
b
выражений.
a b a b a
b
Чему научились?
2
2
12

13.

Ф о р м ул ы с о к р а ще н н о го у м н оже н и я
Представьте
произведения
в виде многочлена:
4
2
2
(3 x 1) (3 x 1) 9 x 1
1) 9bx 1
25a
(5(3
ax
b ) 1)(b (3
5xa )
6
6
(0, 4m3 7 n32 ) (7 n 23 0, 4m3 ) 49n 4 2 0,16m
2
3
3
2
2
6
4
(5a b ) (b 5a) 25a b
4
6
3
2
2
3
(0, 4m 7 n ) (7 n 0, 4m ) 49n 0,16m
( 3 x) ( 3 x) 16 y 2 9 x 2
Впишите вместо знака * одночлен так, чтобы
получилось тождество:
( 3 x) ( 3 x) 16 y 9 x
2
2
* = 4y
13

14.

А теперь рассмотрим еще один любопытный факт,
тоже связанный с нашей новой формулой.
Возьмем несколько «троек» любых, но
последовательных целых чисел, например
3; 4; 5;
9; 10; 11;
Сравните в каждой из них квадрат среднего числа и
произведение предыдущего и последующего целых
чисел.
Вывод: Квадрат среднего числа на 1 больше произведения
предыдущего и последующего целых чисел.
Это случайное совпадение или
закономерность?
Попробуйте рассуждать в общем виде .
14

15.

Три любых последовательных целых числа
можно записать в виде : n-1; n; n+1. Теперь
составим выражения для квадрата среднего
числа и произведения крайних чисел. Получаем
2
2
ожидаемый
вывод:
n ;(n 1) (n 1) n 1
n ;(n 1) (n 1) n 1
2
2
Квадрат среднего числа на 1 больше произведения
предыдущего и последующего целых чисел.
15

16.

Страничка повторения
Докажите
тождество:
2
(a b) 4ab (a b) 2
2
2
(a b) 2 (4a
ab ba)2 2
2ab
b
4
ab
4ab (a b)
2 b 2 (a b)22
a 2 2ab
(a b) 4ab a 2ab b 4ab
2
2
2
2
a ( x 27)ab ( x b5)( x (19)
a b)
2
2
2
2
( xДокажите,
7) ( x 5)( xчто
19)значение
x 14 x 49выражения
x 14 x 95 не зависит от х
144
2
( x 7) ( x 5)( x 19)
2
2
2
( x 7) ( x 5)( x 19) x 14 x 49 x 14 x 95
144
16

17.

Ф о р м ул ы с о к р а ще н н о го у м н оже н и я
Страничка домашнего задания:
1)Изучить с помощью
презентации тему;
2) выполнить в тетради все
тренировочные задания из
презентации;
3) для закрепления выполнить:
1 группа-№854(а-е), № 855( а-в),
№860(д,ж);
2 группа-№854(а-е), № 855(б,в,г)
№ 858(а,б);
3 группа- № 854(г-и),№
855(г,д ,е)
№ 858(в,г), № 860(ж,з).
Б
17