Similar presentations:
В царстве формул сокращенного умножения. Математический диктант
1.
a b2
a 2 ab b
2
2
2
a 2 ab b a b
2
2
В царстве формул
Сокращенного
умножения
a 2 ab b a b
2
2
2
a b
2
a 2 ab b
2
2
1
2.
Какие формулысокращенного умножения
Вы знаете?
2
3.
Формулы сокращённого умножения1) Квадрат суммы двух выражений
1) a b a 2 ab b
2
2 ) a b a 2 ab b
2
2
2
2) Квадрат разности двух выражений
2
2
3) Разность квадратов двух выражений
a b (a b) (a b)
2
2
Сумма кубов двух выражений
a b ( a b ) ( a ab b )
3
3
2
2
Разность кубов двух выражений
a b ( a b ) ( a ab b )
3
3
2
2
4.
а 2аb b2
а b
2
а b
a b а
2
а 2аb b
аb b
а b
3
3
а b
2
2
а b а b
2
2
2
2
a b а
2
аb b
а b
3
2
3
2
5.
Формулы сокращённого умноженияа b а b а b
2
2
а b
а 2аb b
2
а b
а 2аb b
2
2
2
2
2
а b a b а 2 аb b 2
3
3
2
2
а b a b а аb b
3
3
6. Квадрат суммы двух выражений равен…
Закончите формулировкуКвадрат суммы двух выражений
равен…
…квадрату первого выражения, плюс
удвоенное произведение первого и
второго выражений, плюс квадрат
второго выражения.
a b
2
a 2 ab b
2
2
7. Квадрат разности двух выражений равен…
Закончите формулировкуКвадрат разности двух выражений
равен…
…квадрату первого выражения, минус
удвоенное произведение первого и
второго выражений, плюс квадрат
второго выражения.
a b
2
a 2 ab b
2
2
8. Произведение разности двух выражений на их сумму равно…
Закончите формулировкуПроизведение разности двух
выражений на их сумму равно…
…разности квадратов
этих выражений.
2
2
(a-b)(a+b)= a -b
9. Разность квадратов двух выражений равна…
Закончите формулировкуРазность квадратов двух выражений
равна…
…произведению разности
этих выражений на их
сумму.
a b (a b) (a b)
2
2
10. Сумма кубов двух выражений равна…
Закончите формулировкуСумма кубов двух выражений равна…
…произведению суммы этих
выражений и неполного
квадрата их разности.
a b ( a b ) ( a ab b )
3
3
2
2
11. Разность кубов двух выражений равна…
Закончите формулировкуРазность кубов двух выражений
равна…
…произведению разности
этих выражений и неполного
квадрата их суммы.
a b (a b) (a ab b )
3
3
2
2
12. Найдите ошибки:
НАЙДИТЕ ОШИБКИ:2
у)
(в = в - 2ву +
2
2
(7 + с) = 49 +- 14с + с
2
2
(р - 10) = р - 20р + 100
2
2
(2а + 1) = 4а + 42а + 1
2
2
у
13.
Математическийдиктант
13
14. Математический диктант
Запишите:1. квадрат числа а;
2. удвоенное число b;
3. Сумму х и у:
4. сумму квадрата х и куба у;
5. удвоенное произведение а и b;
6. утроенное произведение с и d;
7. квадрат суммы а и b;
8. квадрат разности х и у;
9. произведение b и квадрата а;
10. произведение куба а и удвоенного числа b;
.
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
15. Математический диктант
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
a b a b
a2
2b
x+y
x2 + y 3
2ab
3cd
(a + b)2
(x-y)2
b.a2
a3.2b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
16. Смотри, не ошибись!
СМОТРИ, НЕ ОШИБИСЬ!2
2
2
у
y
(х ... у) = х - 2х + ...
3x -5y
- 30xy
(...
...)2 = 9х2 ...
... + 25у2
2y ...
- 7x
+ 49х2
(...
...)2 = 4y
...2- 28ху ...
(х -10y
... )2 = x...2 ...
- 20ху...
+ ...
100y2
2
25a2 + 10ab
… + b2 = (…
…
…)
5a + b
17.
Творческоезадание
17
18. Расширение знаний по формулам сокращенного умножения
19. Проект № 1
• Цель проекта: научиться возводить в квадратсумму трёх, четырёх, и т.д. слагаемых.
(а+в+с+d)2
(а+в+с)2
(а+в+с+d+e)2
(а+в+с+d+ e+k)2
19
20. Возводить в квадрат сумму трёх, четырёх, и более слагаемых
(а+b+с+d)2 ==((a+ b)+(c+ d))2=
=(a+ b)2 + 2(a+ b)(c+ d)+(c+ d)2 =
=a2+ 2ab+ b2+ 2ac+ 2ad+ 2bc+ 2bd+ c2+ 2cd+ d2=
=a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd
20
21. (а + b + с + d)2 = a2+b2+c2+d2+2ab+2ac+2ad+2bc+2bd+2cd
• ВЫВОД: квадрат суммы трёх, четырёхи более чисел равен сумме квадратов
каждого из этих чисел плюс удвоенные
произведения каждого из этих чисел на
числа, следующие за ним.
22. Вычислите:
2(3х+4у+5z) =
=9x2 +16y2 +25z2 +24xy +30xz + 40yz
22
23. Проект № 2
• Цель проекта: научиться возводитьдвучлен в любую натуральную
степень.
23
24.
4(а+в)
=
2
b) (a+
2
b) =
(a+
2
2
2
2
= (a + 2ab+ b )(a + 2ab+ b )=
4
3
=a +4a b+
2
2
3
4
6a b +4ab +b
24
25.
4(а+b)
=
2
2
b) ) =
=((a+
2
2
2
=( a + 2ab+ b ) =
= а4+4а2b2+b4+4a3b+2a2b2+4ab3 =
4
=а
3
2
2
3
4
+4a b+6a b +4ab +b
25
26.
Рассмотримдвучлены:
(а + b)0 = 1
(a + b)1 = 1a +1 b
(a + b)2 =1 a2 + 2ab +1 b2
(a + b)3 =1 a3 + 3a2b + 3ab2 + 1b3
Составим таблицу из их
коэффициентов:
1
1 1
1 2 1
1 3 3 1
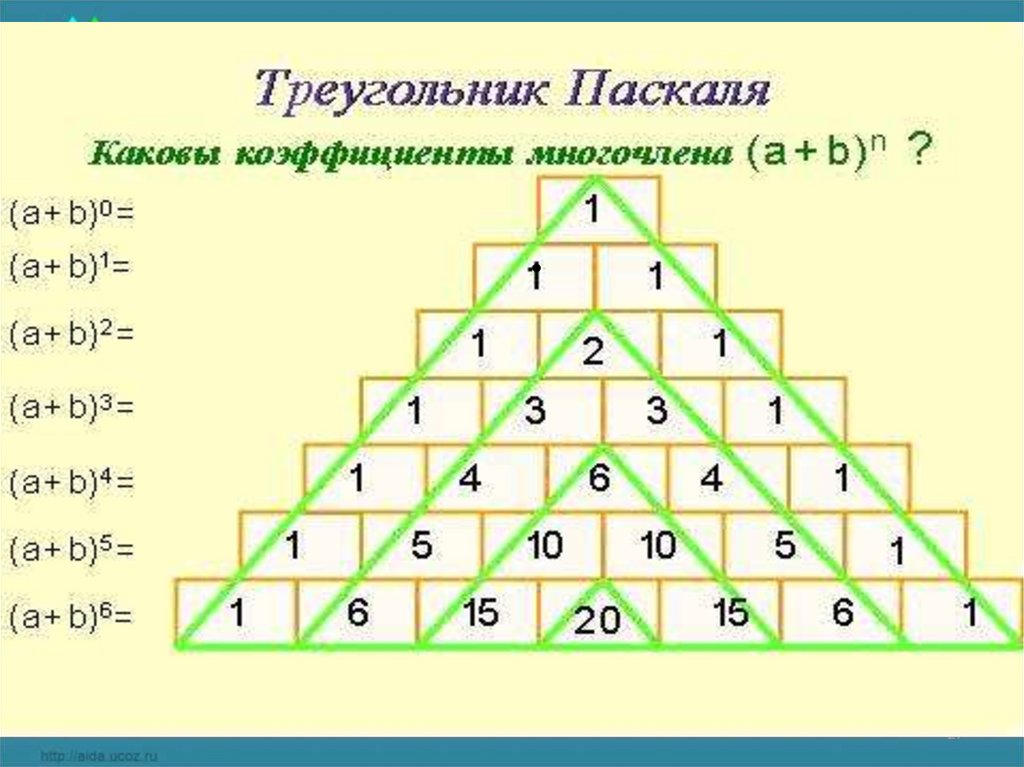
27.
27
28. Блез Паскаль (1623 – 1662)
02
11
11-2
2
121-2
3
1331-2
29. Где применяются формулы сокращенного умножения?
• При упрощении выражений.• При разложении выражений на множители.
• При решении уравнений.
• При доказательстве тождеств.
30.
• Применяются в некоторыхматематических фокусах.
• Предлагается кому-нибудь задумать не очень большое
число и возвести его в квадрат. К результату
попросите прибавить удвоенное задуманное число и
ещё единицу. Выяснив окончательный результат, вы
сможете назвать задуманное число. Как найти
задуманное число?
• формула а2 + 2 а + 1 = (а +1)2
30
31. Домашнее задание
1. Повторить формулы сокращенного умножения2. Постройте треугольник Паскаля(тетрадь по
теории)
3. Возведите в степень (а + b)5
4. Возводить в квадрат сумму пяти слагаемых
(а+b+с+d +e)2
5. Решите по учебнику
6. Выписать ФСУ до 5 степени в тетрадь по
теории
a b a b a 2 b2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
32.
Спасибо заурок!
33. Найдите квадрат выражения:
2у)
а) (а – х +
2
б) (а – b – с)
34. Вычислите:
2195
1)
2
2) 488
35. a2 = а2 – b2 + b2 = (a – b)(a + b) + b2, где b – дополнение числа а до круглого числа.
Пример.Вычислите 9862
1. Круглое число 1000.
а = 986, b = 14, а + b = 1000, a – b = 972.
2. 9862 = 972 1000 + 142 = 972000 + 196 = 972196.
36. Исторические сведения.
• Формулы сокращенного умножения былиизвестны еще 4000 лет назад. Ученые Древней
Греции представляли величины не числами или
буквами, а отрезками прямых. Вместо
«произведение а в» говорилось «прямоугольник,
содержащийся между а и в»,вместо а2 «квадрат на
отрезке а».В книге Евклида «Начала» правило
квадрата суммы выражается так: «если прямая
линия как-либо рассечена точкой С, то квадрат на
всей прямой равен квадратам на отрезках вместе с
дважды взятым прямоугольником , заключенным
между отрезками.



































 mathematics
mathematics








