Similar presentations:
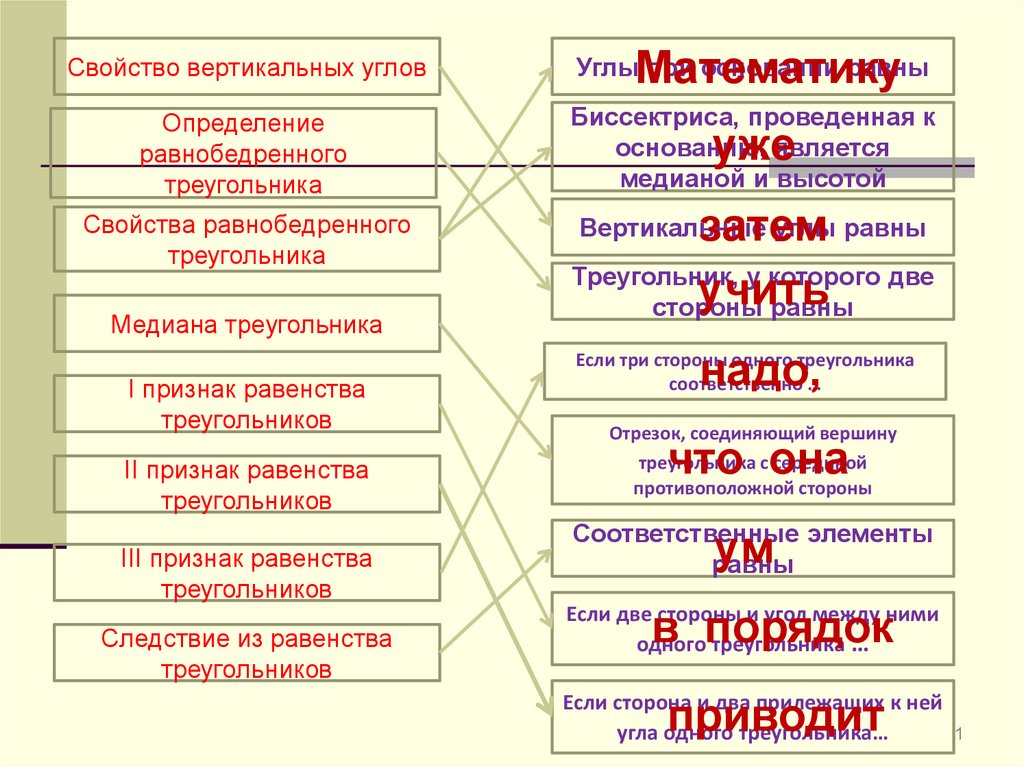
Свойство вертикальных углов
1.
МатематикуСвойство вертикальных углов
Углы при основании равны
Определение
равнобедренного
треугольника
Биссектриса, проведенная к
основанию, является
медианой и высотой
Свойства равнобедренного
треугольника
затем
Треугольник, у которого две
учить
стороны
равны
Медиана треугольника
I признак равенства
треугольников
II признак равенства
треугольников
III признак равенства
треугольников
Следствие из равенства
треугольников
уже
Вертикальные углы равны
надо,
Если три стороны одного треугольника
соответственно …
Отрезок, соединяющий вершину
треугольника с серединой
противоположной стороны
что она
Соответственные элементы
равны
ум
в порядок
Если две стороны и угол между ними
одного треугольника …
приводит
Если сторона и два прилежащих к ней
угла одного треугольника…
1
2. Девиз урока
«Математику уже затемучить надо, что она ум
в порядок приводит»
М.В. Ломоносов
2
3. Тема урока:
Признаки равенстватреугольников.
Решение задач.
4.
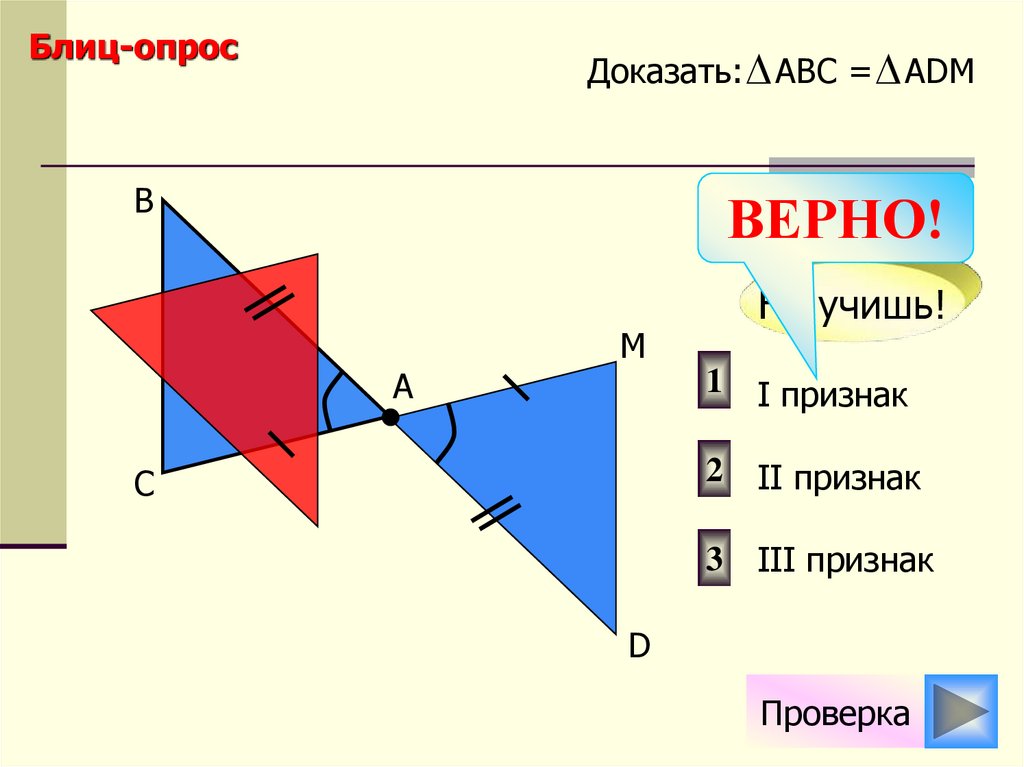
Блиц-опросДоказать: АВС = АDМ
В
ВЕРНО!
А
М
Не учишь!
1 I признак
2 II признак
С
3 III признак
D
Проверка
5.
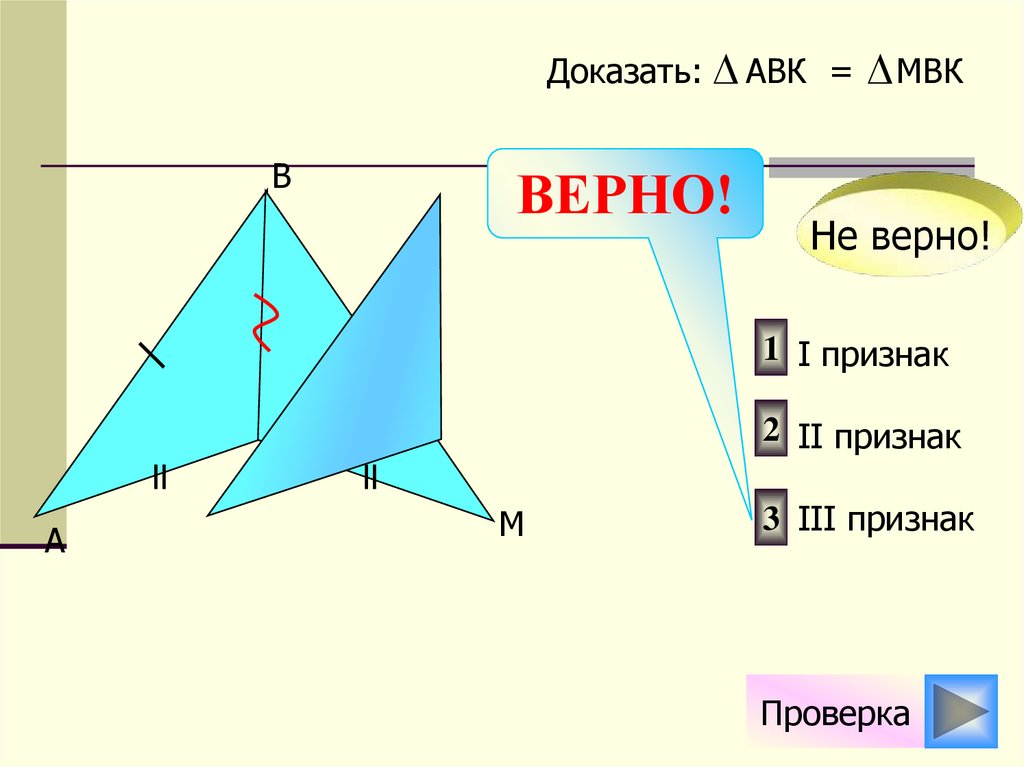
Доказать: АВК =B
ВЕРНО!
МBК
Не верно!
1 I признак
2 II признак
K
A
M
3 III признак
Проверка
6.
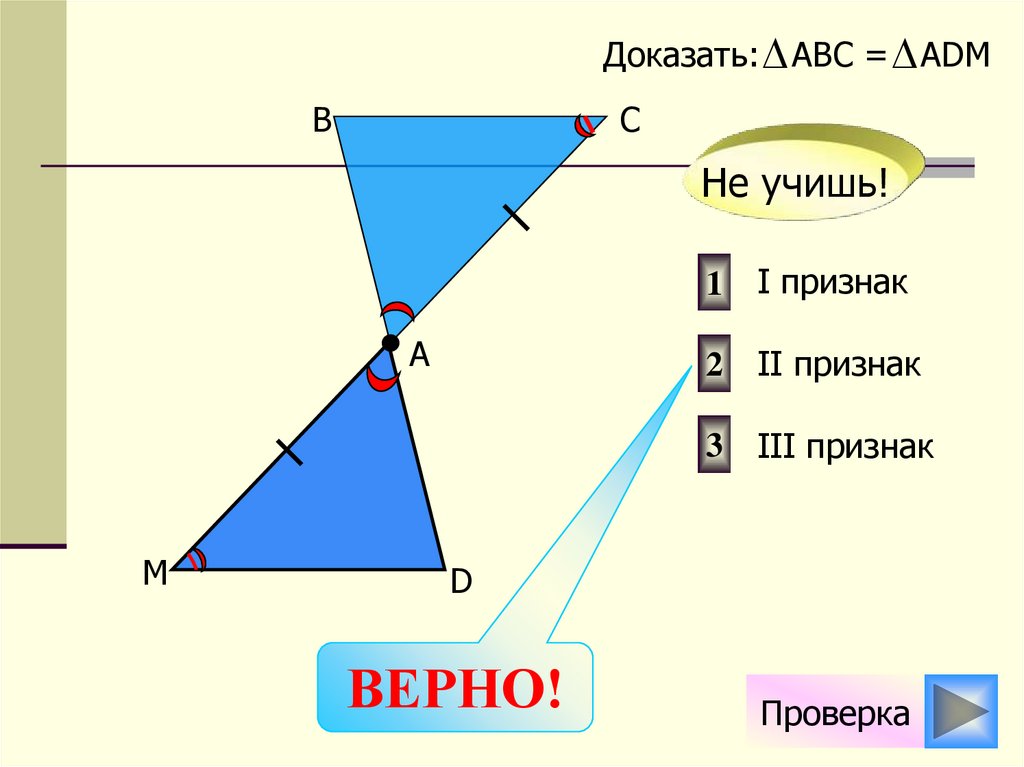
Доказать: АВС = АDМВ
С
Не учишь!
1 I признак
А
2 II признак
3 III признак
М
D
ВЕРНО!
Проверка
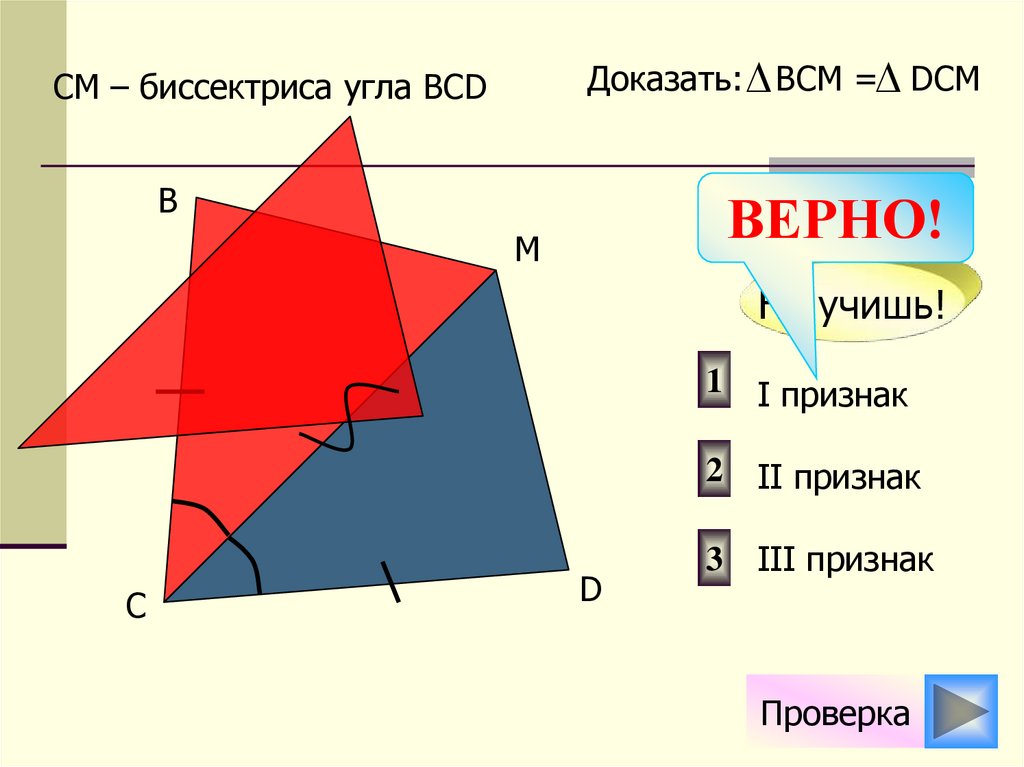
7.
Доказать: ВСМ = DСМСМ – биссектриса угла ВСD
В
ВЕРНО!
М
Не учишь!
1 I признак
2 II признак
С
D
3 III признак
Проверка
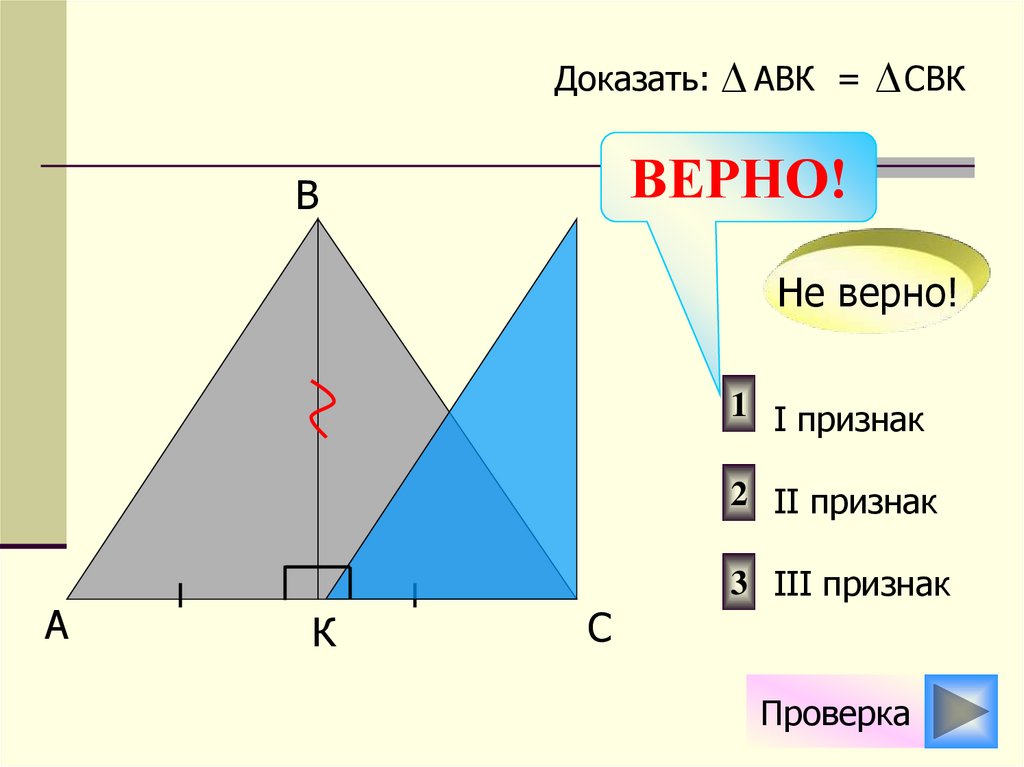
8.
Доказать:АВК
=
СBК
ВЕРНО!
В
Не верно!
1 I признак
2 II признак
A
К
С
3 III признак
Проверка
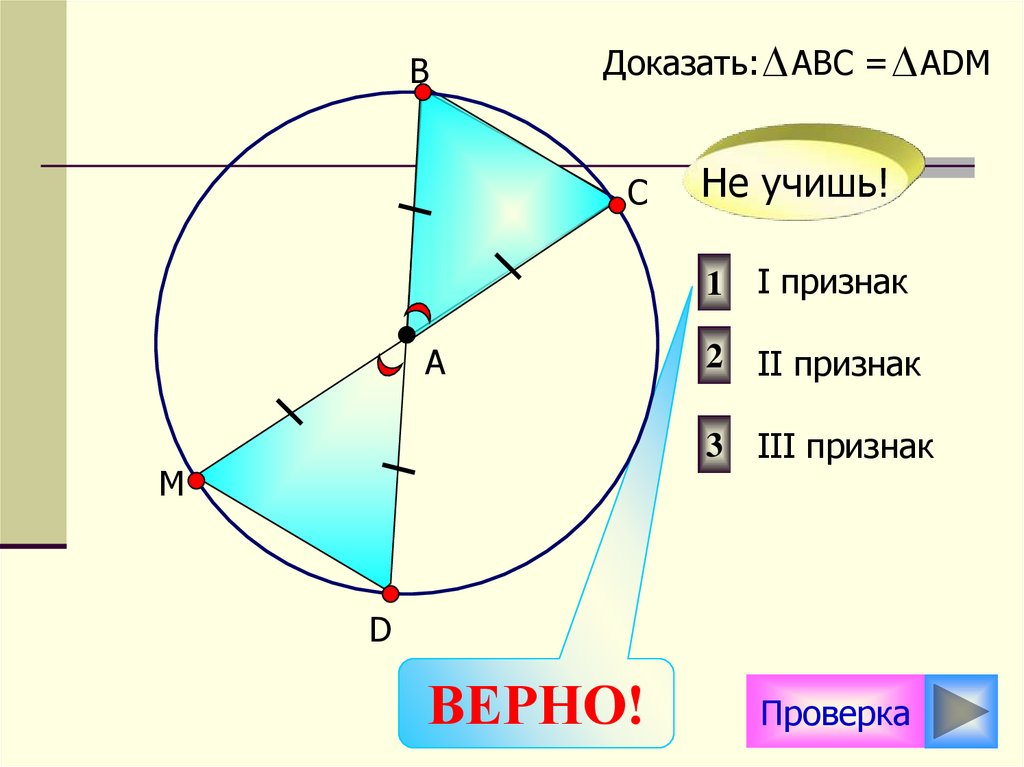
9.
ВДоказать: АВС = АDМ
С
Не учишь!
1 I признак
А
2 II признак
3 III признак
М
D
ВЕРНО!
Проверка
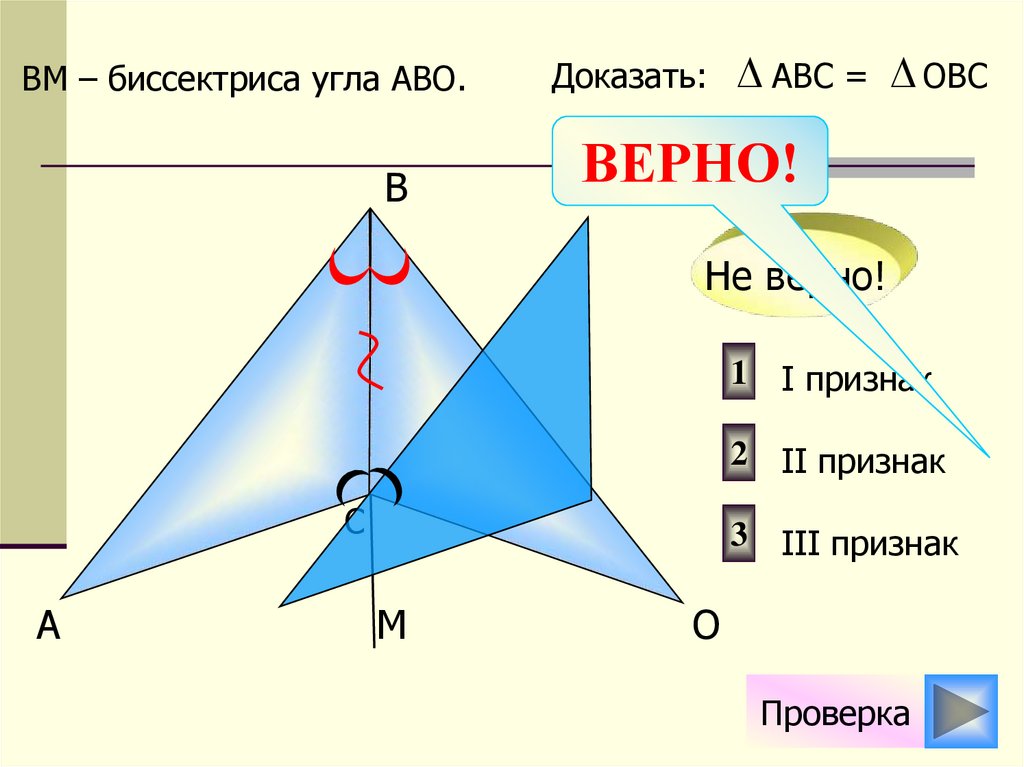
10.
ВM – биссектриса угла АВО.B
Доказать:
АВС = ОВС
ВЕРНО!
Не верно!
1 I признак
2 II признак
С
А
3 III признак
М
О
Проверка
11.
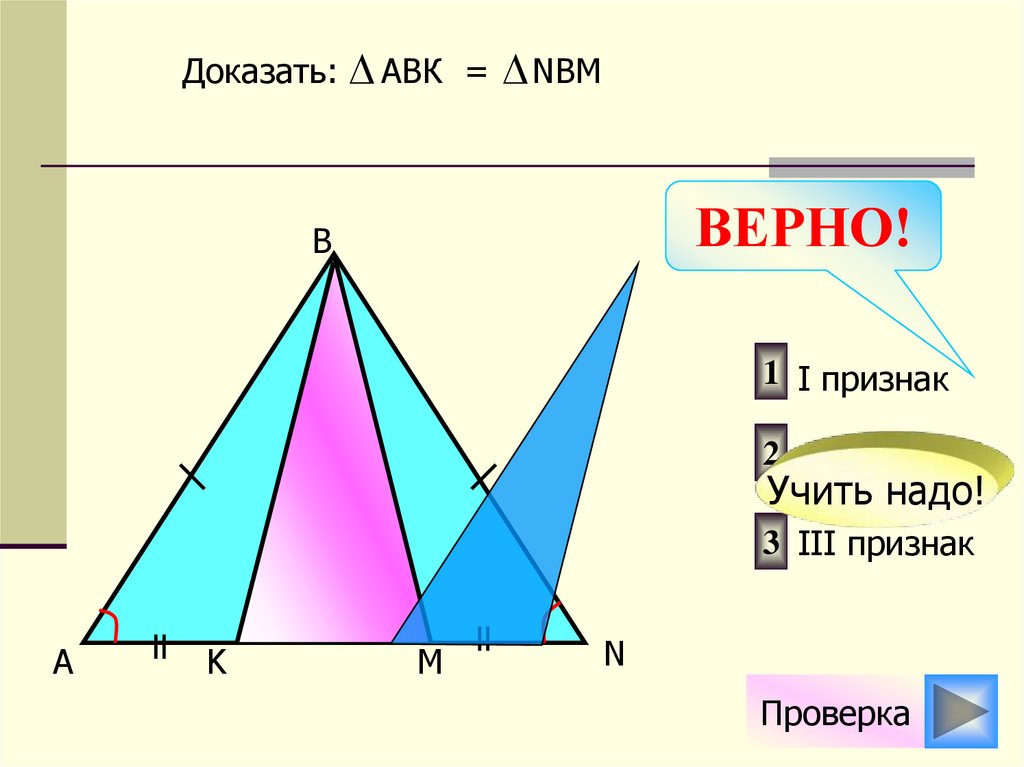
Доказать:АВК
=
NBM
ВЕРНО!
B
1 I признак
2 II признак
Учить надо!
3 III признак
A
K
M
N
Проверка
12.
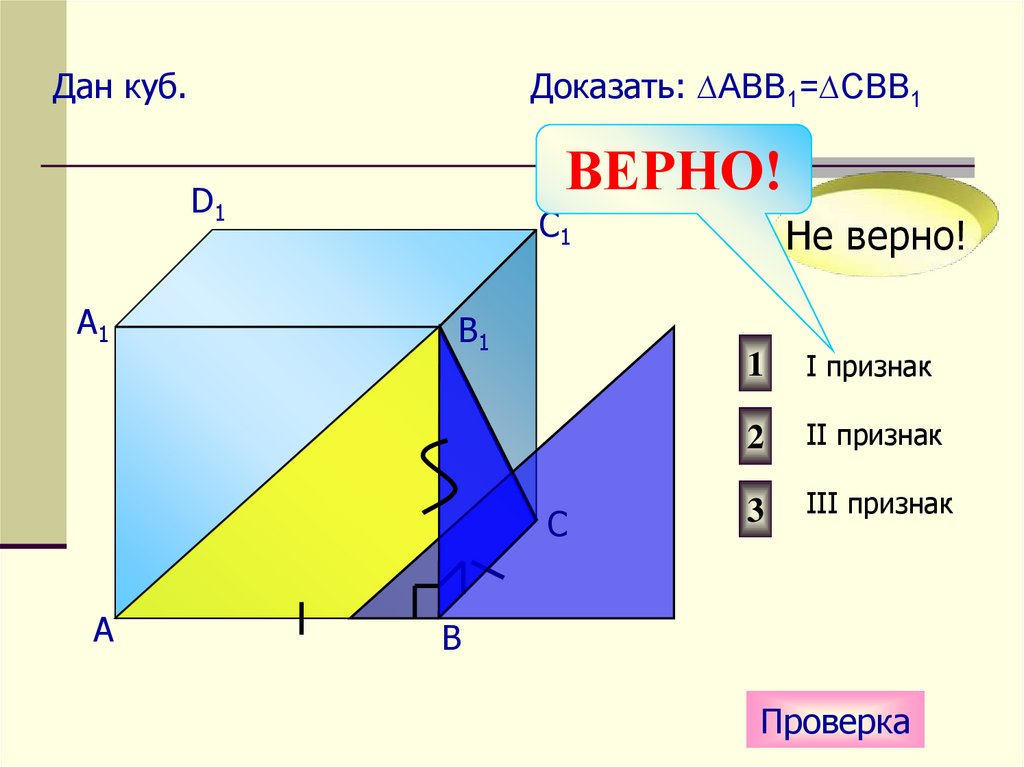
Дан куб.Доказать: ∆АВВ1=∆СВВ1
ВЕРНО!
D1
А1
C1
B1
С
А
Не верно!
1
I признак
2
II признак
3
III признак
В
Проверка
13. Решение задач
по готовым чертежам14.
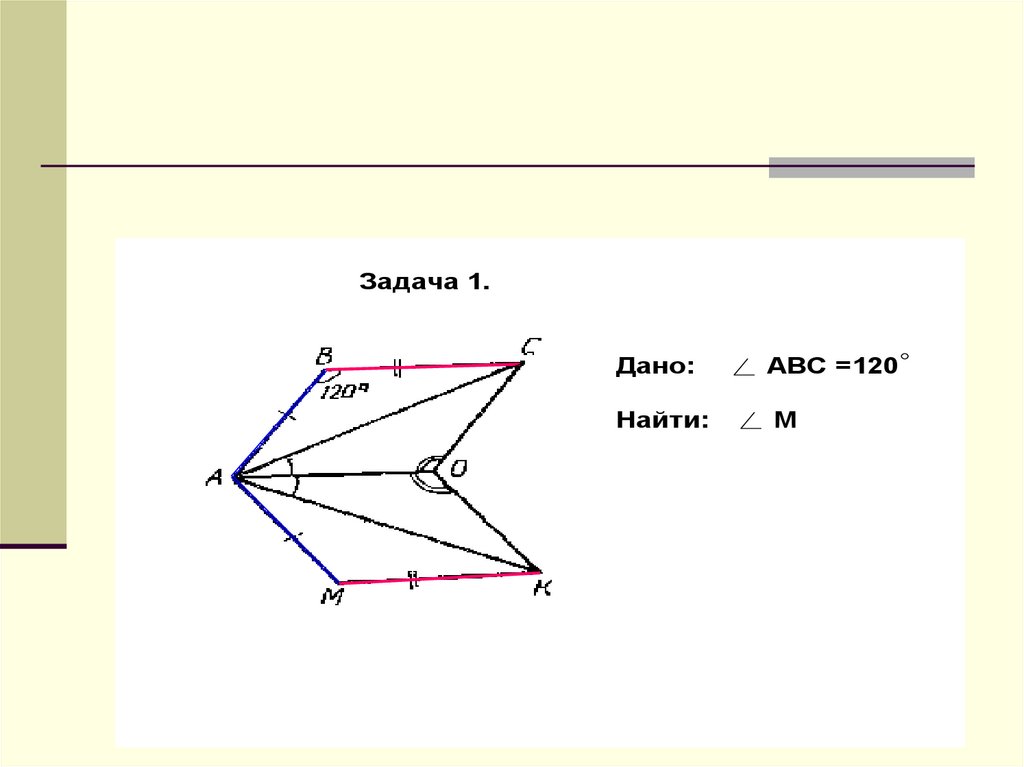
Задача 1.Дано:
АВС =120
Найти:
М
15.
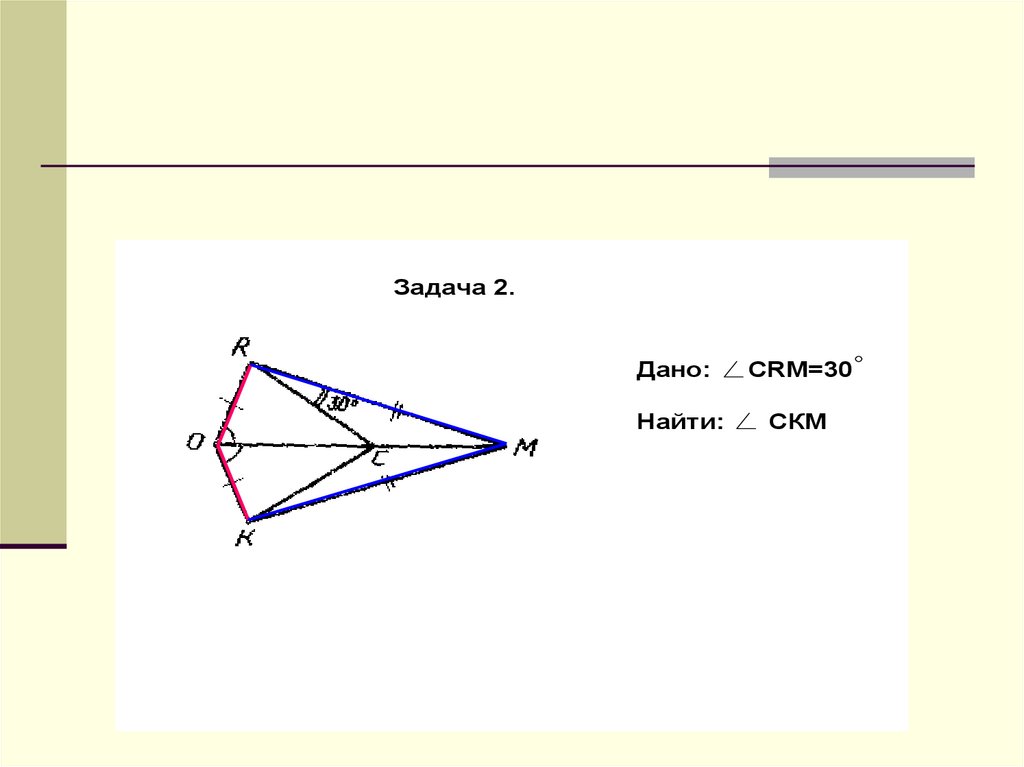
Задача 2.Дано:
Найти:
СRМ=30
СКМ
16.
Виртуальная экскурсия17.
Начиная игру в бильярд, необходимо расположить шары ввиде треугольника. Для этого используют специальную
треугольную рамку.
18.
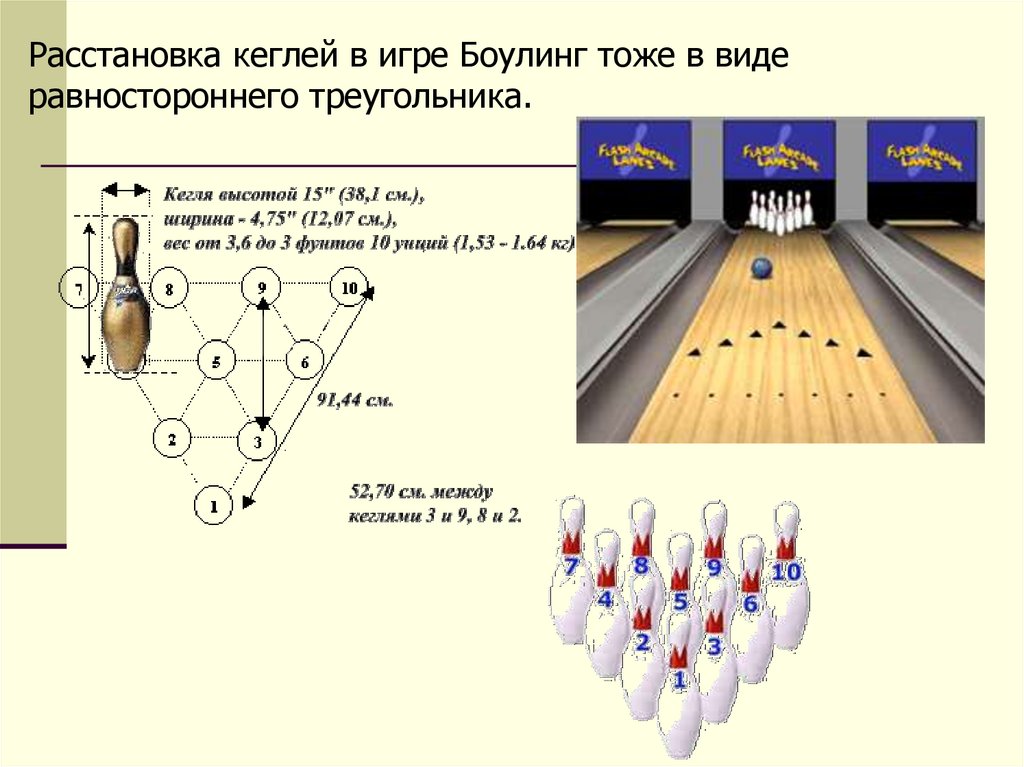
Расстановка кеглей в игре Боулинг тоже в видеравностороннего треугольника.
19.
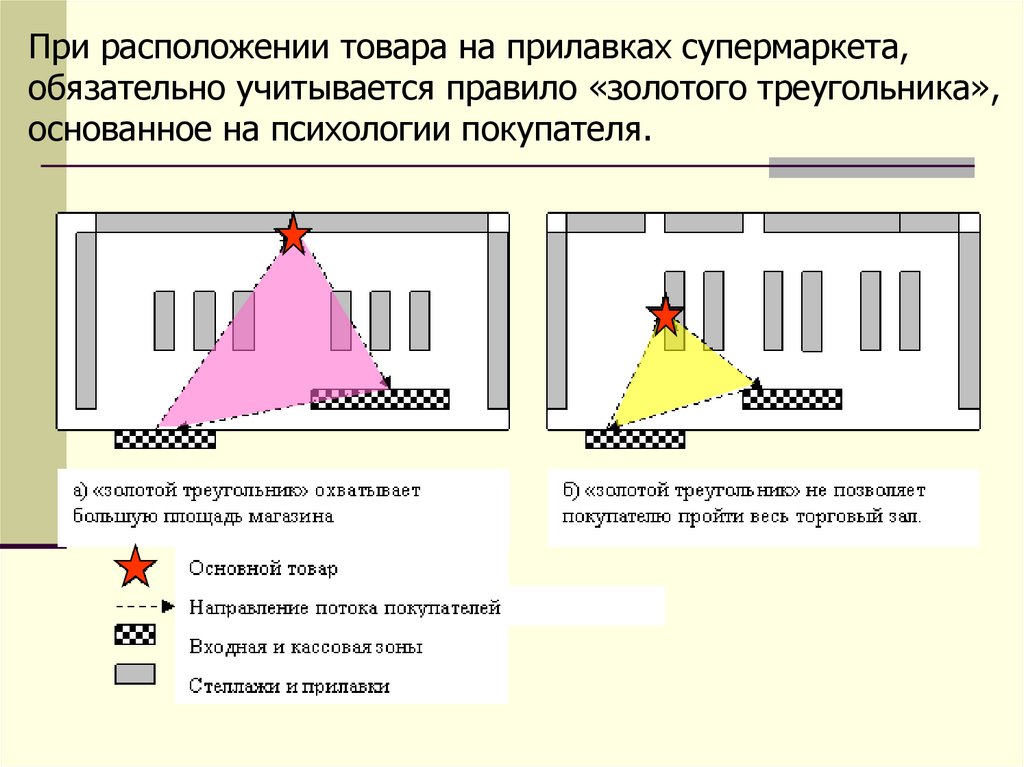
При расположении товара на прилавках супермаркета,обязательно учитывается правило «золотого треугольника»,
основанное на психологии покупателя.
20.
РасположениеБермудского
треугольника
21.
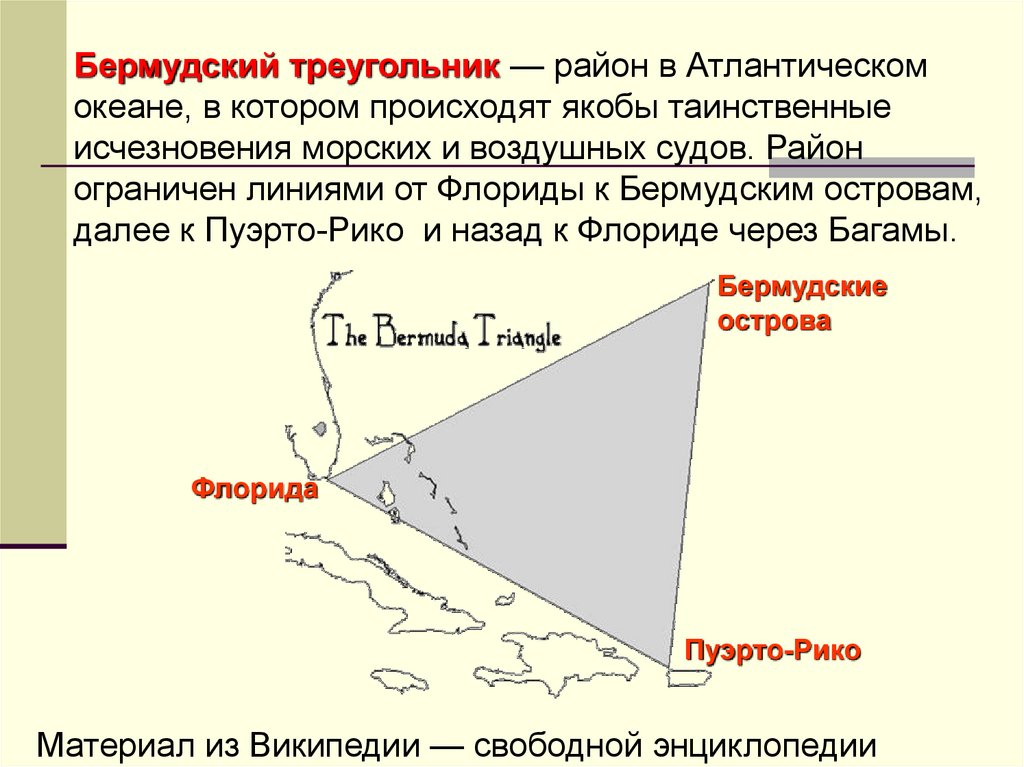
Бермудский треугольник — район в Атлантическомокеане, в котором происходят якобы таинственные
исчезновения морских и воздушных судов. Район
ограничен линиями от Флориды к Бермудским островам,
далее к Пуэрто-Рико и назад к Флориде через Багамы.
Бермудские
острова
Флорида
Пуэрто-Рико
Материал из Википедии — свободной энциклопедии
22.
Две рейки, у которых два конца скреплены гвоздем.Такая конструкция не является жесткой: сдвигая или
раздвигая концы, мы можем менять угол между ними.
23.
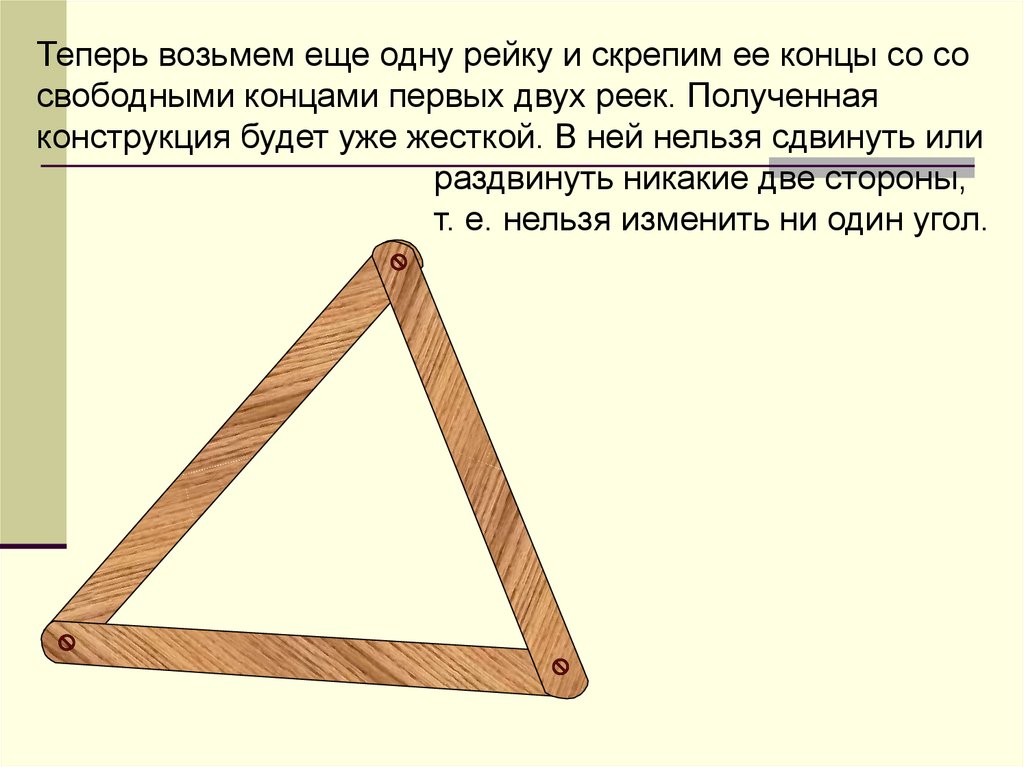
Теперь возьмем еще одну рейку и скрепим ее концы со сосвободными концами первых двух реек. Полученная
конструкция будет уже жесткой. В ней нельзя сдвинуть или
раздвинуть никакие две стороны,
т. е. нельзя изменить ни один угол.
24.
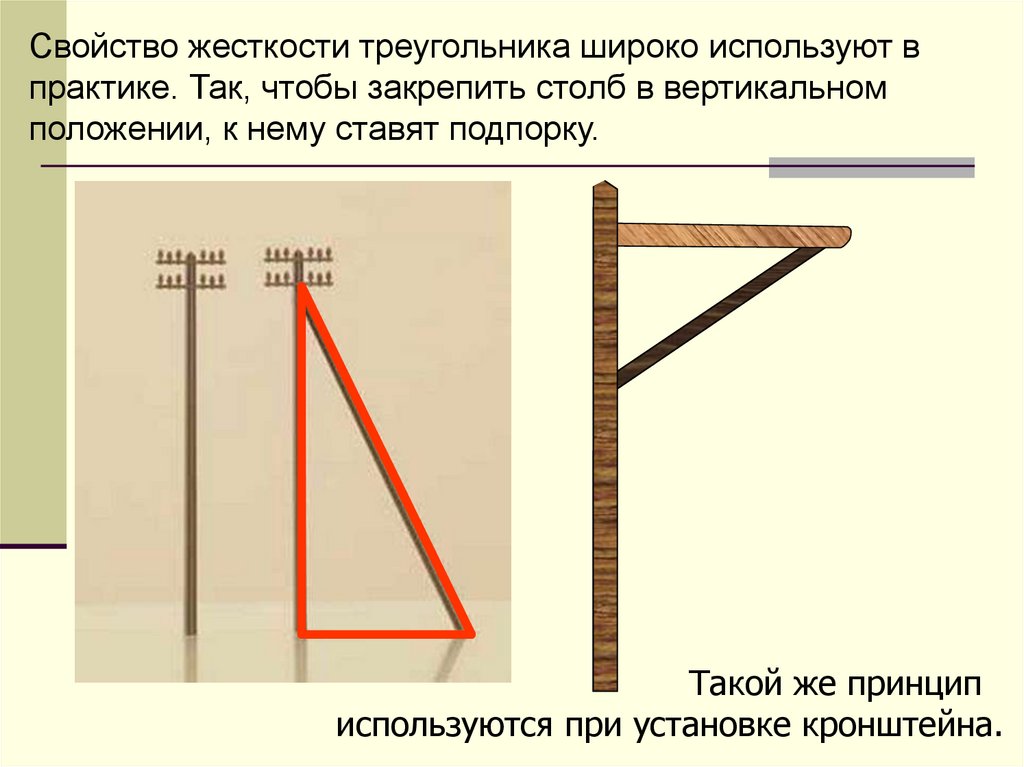
Свойство жесткости треугольника широко используют впрактике. Так, чтобы закрепить столб в вертикальном
положении, к нему ставят подпорку.
Такой же принцип
используются при установке кронштейна.
25.
19 марта 2007 года Шуховскойбашне на Шаболовке исполнилось
85 лет.
Свойство жесткости
треугольника широко
используют в практике при
строительстве железных
конструкций.
26.
Высоковольтные линии электропередачи.Треугольники делают конструкции надежными.
27.
Треугольники в конструкции мостов.28.
Треугольник полярный, треугольникхарактеристический. Каких только треугольников нет в
математике.
В глубокой древности вместе с астрономией появилась
появилась наука – тригонометрия.
Слово «тригонометрия»
произведено от греческих
«треугольник»
«меряю»
Буквальное значение – «наука об измерении
треугольников»
29.
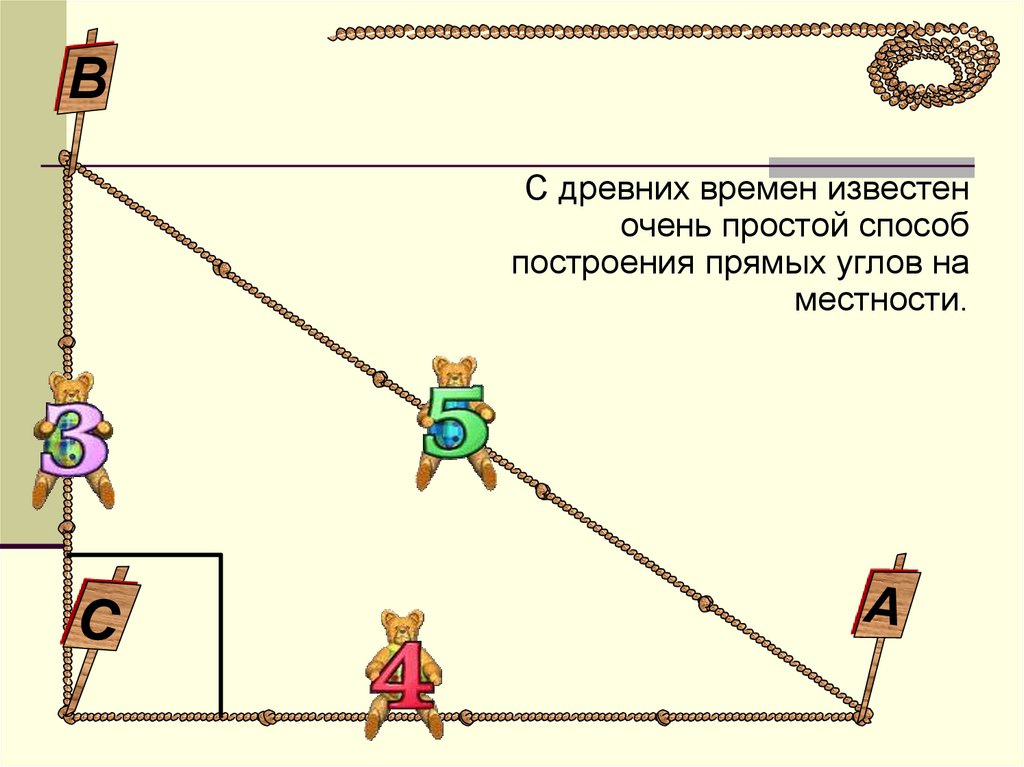
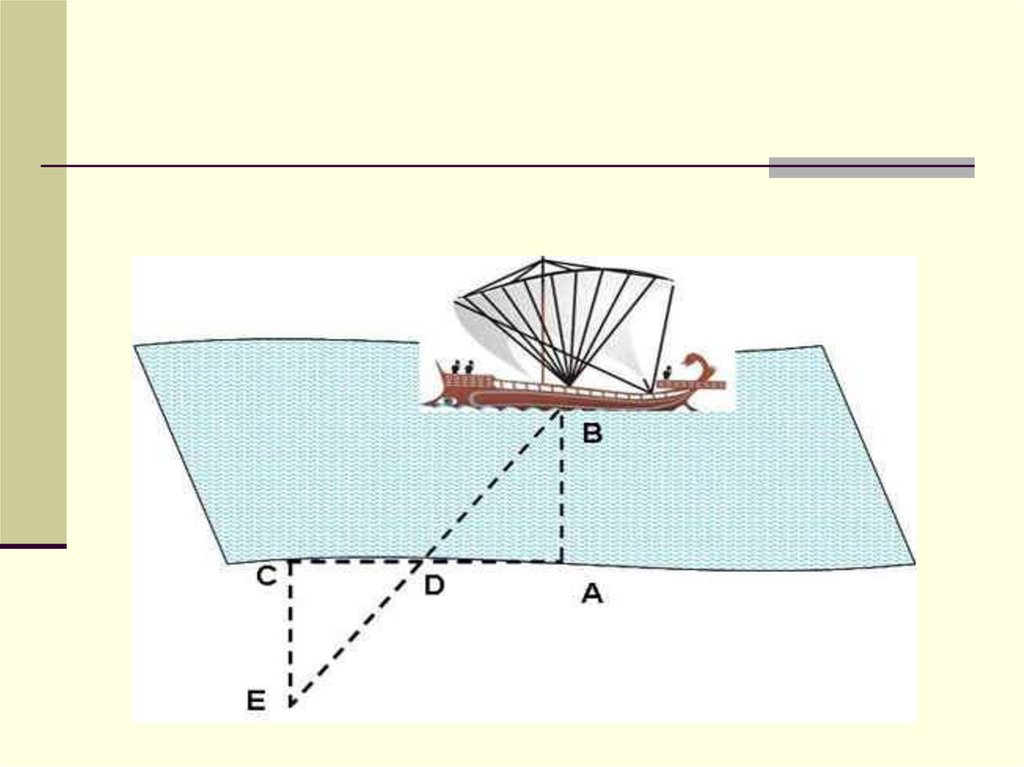
ВС древних времен известен
очень простой способ
построения прямых углов на
местности.
30.
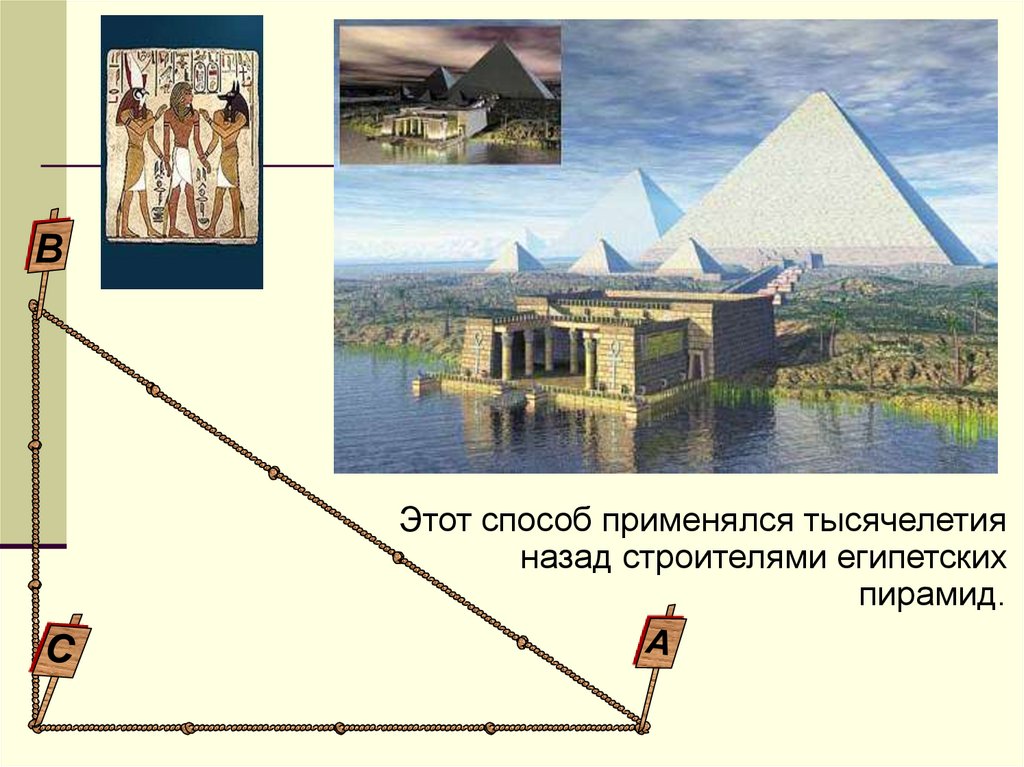
ВЭтот способ применялся тысячелетия
назад строителями египетских
пирамид.
31.
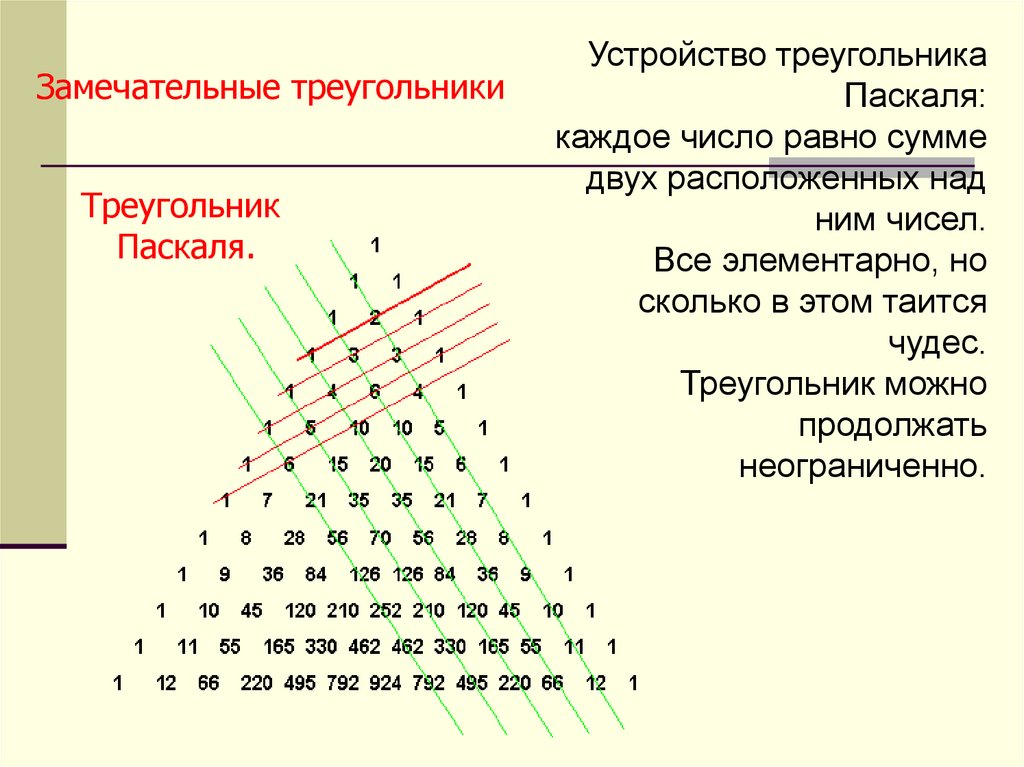
Замечательные треугольникиТреугольник
Паскаля.
Устройство треугольника
Паскаля:
каждое число равно сумме
двух расположенных над
ним чисел.
Все элементарно, но
сколько в этом таится
чудес.
Треугольник можно
продолжать
неограниченно.
32.
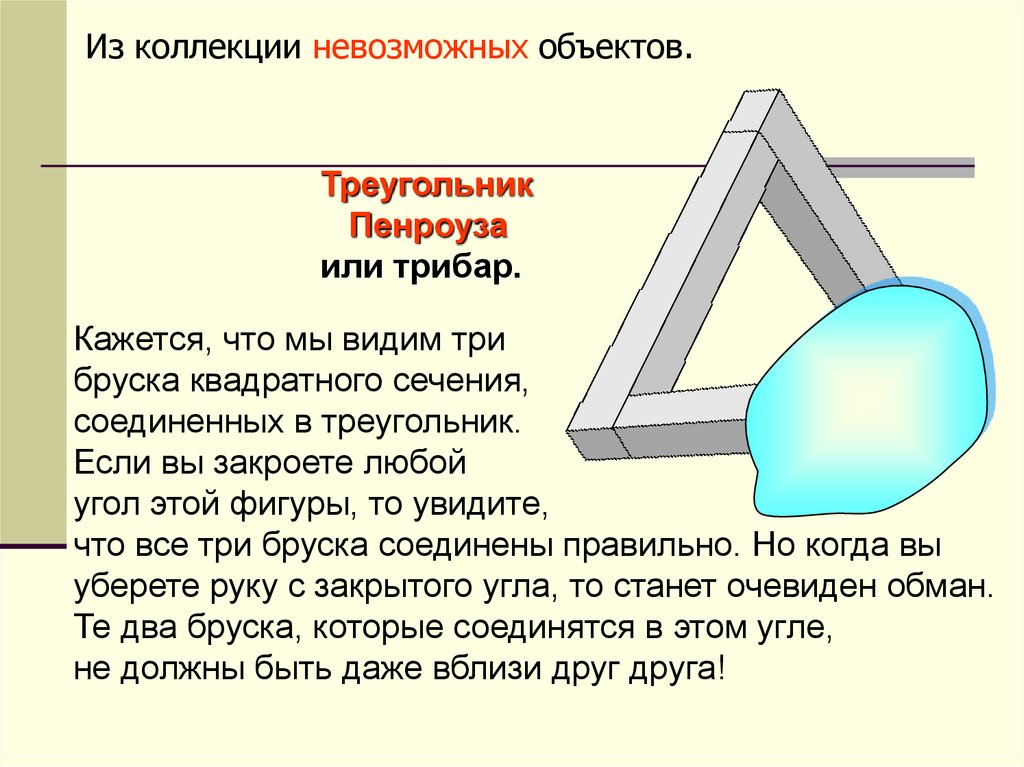
Из коллекции невозможных объектов.Треугольник
Пенроуза
или трибар.
Кажется, что мы видим три
бруска квадратного сечения,
соединенных в треугольник.
Если вы закроете любой
угол этой фигуры, то увидите,
что все три бруска соединены правильно. Но когда вы
уберете руку с закрытого угла, то станет очевиден обман.
Те два бруска, которые соединятся в этом угле,
не должны быть даже вблизи друг друга!
33.
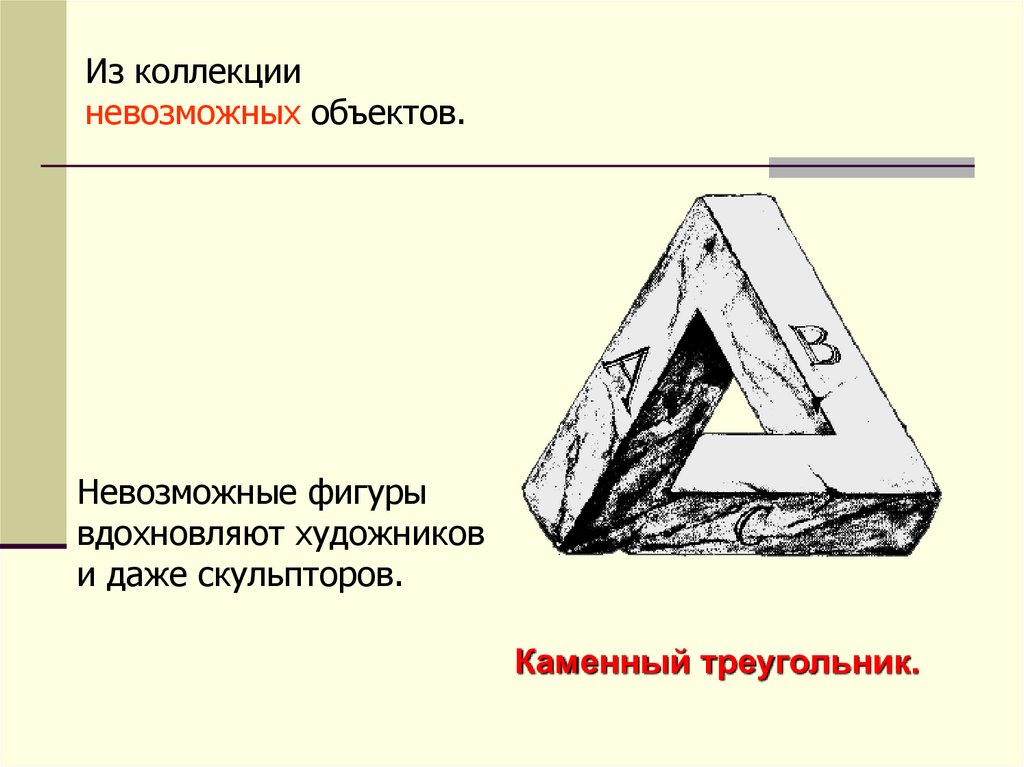
Из коллекцииневозможных объектов.
Невозможные фигуры
вдохновляют художников
и даже скульпторов.
Каменный треугольник.
34. Самостоятельная работа
Удачи!35. Домашнее задание.
1 уровень №1222 уровень №139
3 уровень №140
придумать задачи на применение
признаков равенства треугольников.














 mathematics
mathematics








