Способы решения систем уравнений с двумя переменными

1. «Учиться можно только весело. Чтобы переваривать знания, надо поглощать их с аппетитом».

Анатоль Франс

2.

3. Диофант ! ?

4. ДИОФАНТ АЛЕКСАНДРИЙСКИЙ /// век н.э. Диофант – один из представителей ученых, который ввел понятие систем уравнений.

5. Тема урока : Способы решения систем уравнений с двумя переменными

Цель урока:
обобщить, систематизировать и закрепить
теоретические знания по данной теме;
закрепить навыки решения систем уравнений
второй степени различными способами,
применяя наиболее рациональные.

6.

Определите степень уравнения
ху 2 у 5
х у 2
х у 0
х 3у 0
2
2
х 3у 4
2

7.

8.

9.

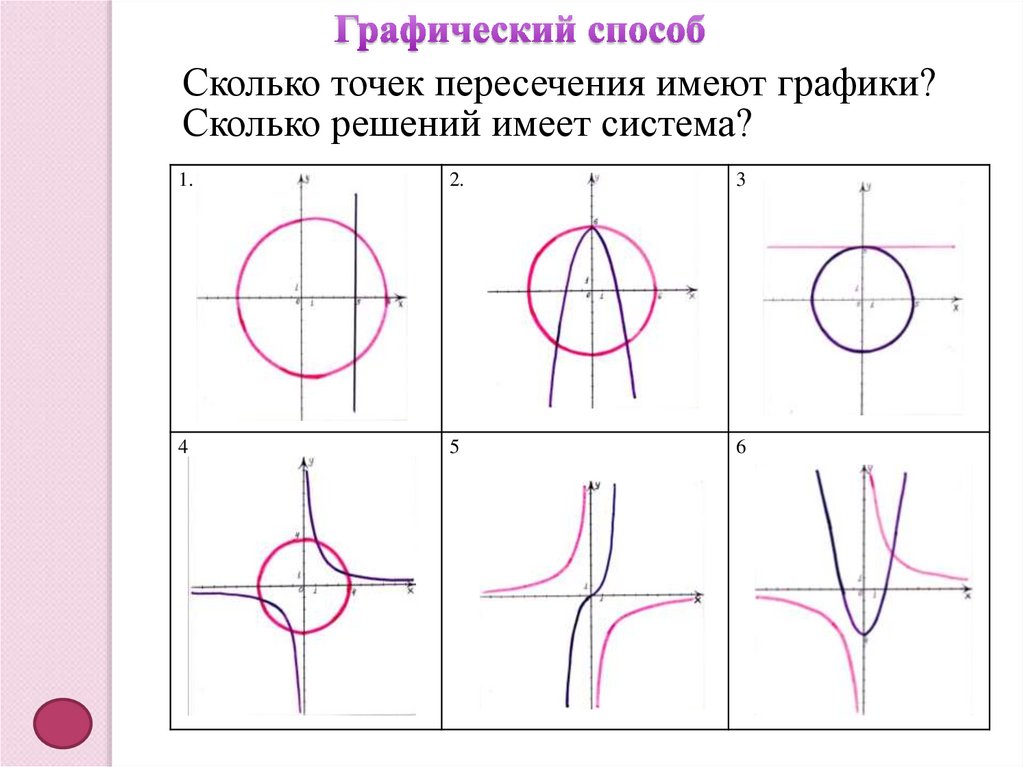
Сколько точек пересечения имеют графики?
Сколько решений имеет система?
1.
2.
3
4
5
6

10.

11.

12.

Выразите одну переменную через другую
4х 2 у 6
х у 7
ху 4
ху 5
3х 6 у 9

13.

Как решить систему
способом сложения
Как записать решение
системы?

14.

Работа по учебнику
№430 (г)
Работа у доски:

15. Умение решать уравнения второй степени используется: 1. В области атомной физики. 2. При расчетах фундаментов строений. 3. При

составлении карт геодезических
съёмок.

16.

Домашнее задание:
№ 452; 453 с.121

17.

18.

построить графики уравнения
в одной координатной
плоскости;
найти координаты точек
пересечения графиков, которые
и будут решением системы

19.

Выражают из какого-нибудь уравнения
системы одну переменную через другую;
Подставляют в другое уравнение
системы вместо этой переменной
полученное выражение;
Решают полученное уравнение с одной
переменной;
Находят соответствующее значение
второй переменной, из подстановки.

20.

Умножают почленно уравнения
системы, подбирая множители так, чтобы
коэффициенты при одной из переменных
стали противоположные числа;
Складывают почленно левые и правые
части уравнений системы;
Решают получившееся уравнение с
одной переменной;
Находят соответствующие уравнения
второй переменной.

21.

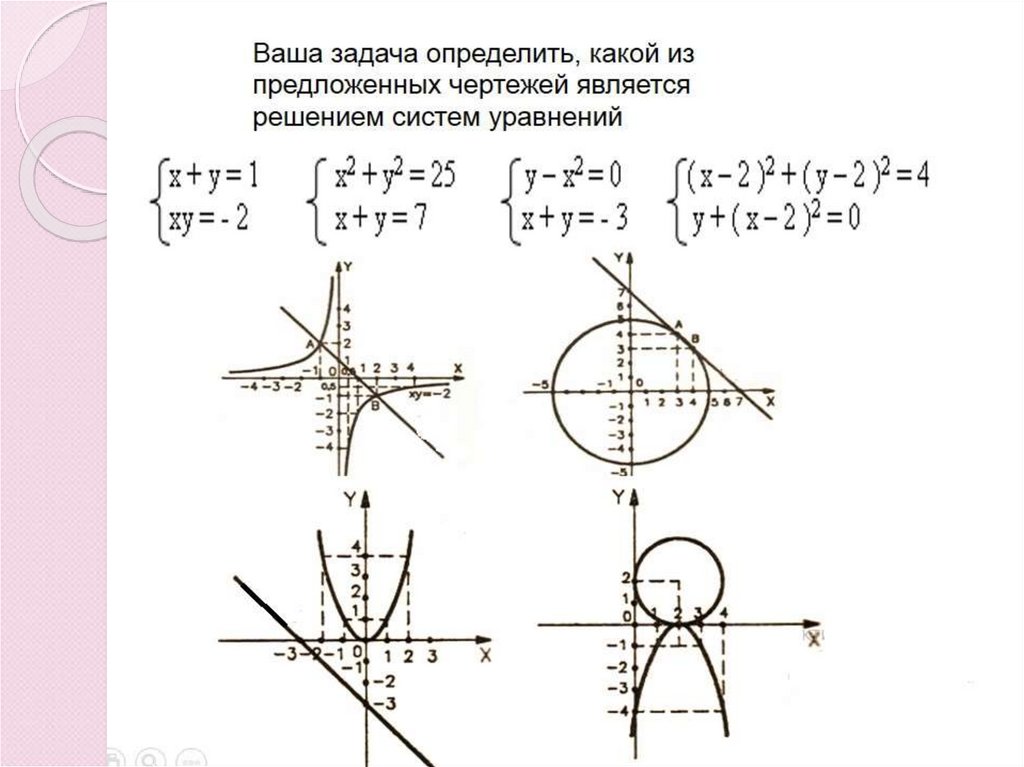
Координаты точек пересечения
удовлетворяют каждому уравнению системы.
Решение системы уравнений, если она
решается графическим способом, записывается
приближенным равенством для значений
переменных.
Количество решений системы уравнений при
графическом способе решения зависит от
количества точек пересечения графиков
уравнений.
Если графики имеют три точки пересечения,
то система имеет три решения.

22.

Если в систему входит уравнение 1-ой
степени, то подстановку получают из
этого уравнения. Если оба уравнения
второй степени, то подстановку получают
из любого.
Решение системы записывается парой
чисел.