Энтропия как мера степени неопределенности

1.

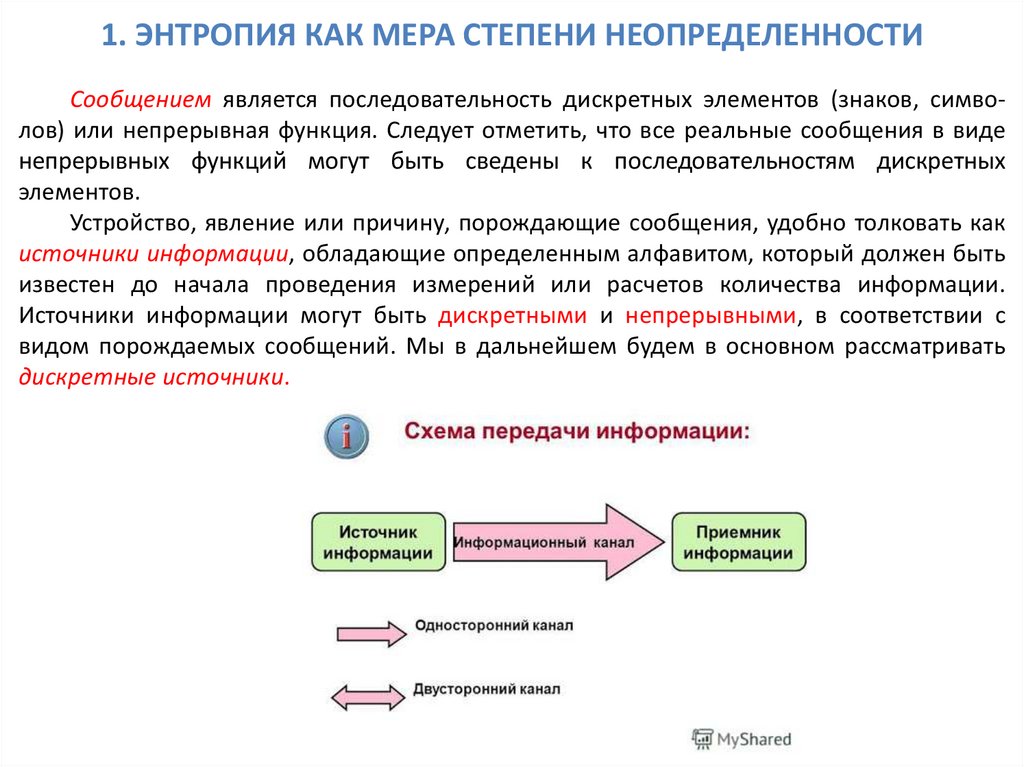
1. ЭНТРОПИЯ КАК МЕРА СТЕПЕНИ НЕОПРЕДЕЛЕННОСТИ
Сообщением является последовательность дискретных элементов (знаков, символов) или непрерывная функция. Следует отметить, что все реальные сообщения в виде
непрерывных функций могут быть сведены к последовательностям дискретных
элементов.
Устройство, явление или причину, порождающие сообщения, удобно толковать как
источники информации, обладающие определенным алфавитом, который должен быть
известен до начала проведения измерений или расчетов количества информации.
Источники информации могут быть дискретными и непрерывными, в соответствии с
видом порождаемых сообщений. Мы в дальнейшем будем в основном рассматривать
дискретные источники.

2.

Дискретный источник обладает конечным алфавитом из М
элементов, обозначаемых х1, х2, … , хi, … , хМ, каждый из которых
характеризуется вероятностью Р(х1), Р(х2), … , Р(хi), …, Р(хМ)
появления в сообщении. То есть мы опять имеем дело со
случайными событиями.
Совокупность элементов и их вероятностей удобно задавать в
виде матрицы:
x1
x2
xM
X
P( x1 ) P( x2 ) P( xM )
P
В большинстве реальных случаев появление элемента хi в
сообщении зависит от того, какой элемент хj был
предшествующим.

3.

Взаимосвязь элементов в сообщении
матрицей условных вероятностей:
P1 (1) P1 (2)
P2 (1) P2 (2)
Px j ( xi ) Pj (i )
Pj (1) Pj (2)
PM (1) PM (2)
P1 (i )
P2 (i )
Pj (i )
PM ( j )
характеризуется
P1 ( M )
P2 ( M )
Pj ( M )
PM ( M )
При отсутствии взаимосвязи элементов:
Px1 ( xi ) Px2 ( xi ) ... PxM ( xi ) P( xi )
Неопределенность выбора элементов хi при создании
сообщения удобно характеризовать энтропией источника H(x).
При независимых элементах:
M
H ( x) P(i ) log( P (i ))
i 1

4.

При зависимых элементах с условными вероятностями сначала
определяется частная условная энтропия, вычисленная по
предыдущей формуле, но в предположении зафиксированного
предыдущего элемента хj:
M
H x j ( x) Pj (i ) log( Pj (i ))
i 1
Величина H(x) случайная, так как случайным является
предшествующий элемент хj. Поэтому для получения полной
энтропии источника необходимо произвести усреднение по
вероятностям появления предшествующих элементов:
M
H ( x) Pj (i ) log( Pj (i )) P( j )
j 1 i 1
M
Это формула средней условной энтропии или просто энтропии
источника, которая учитывает взаимозависимость элементов в
сообщении.

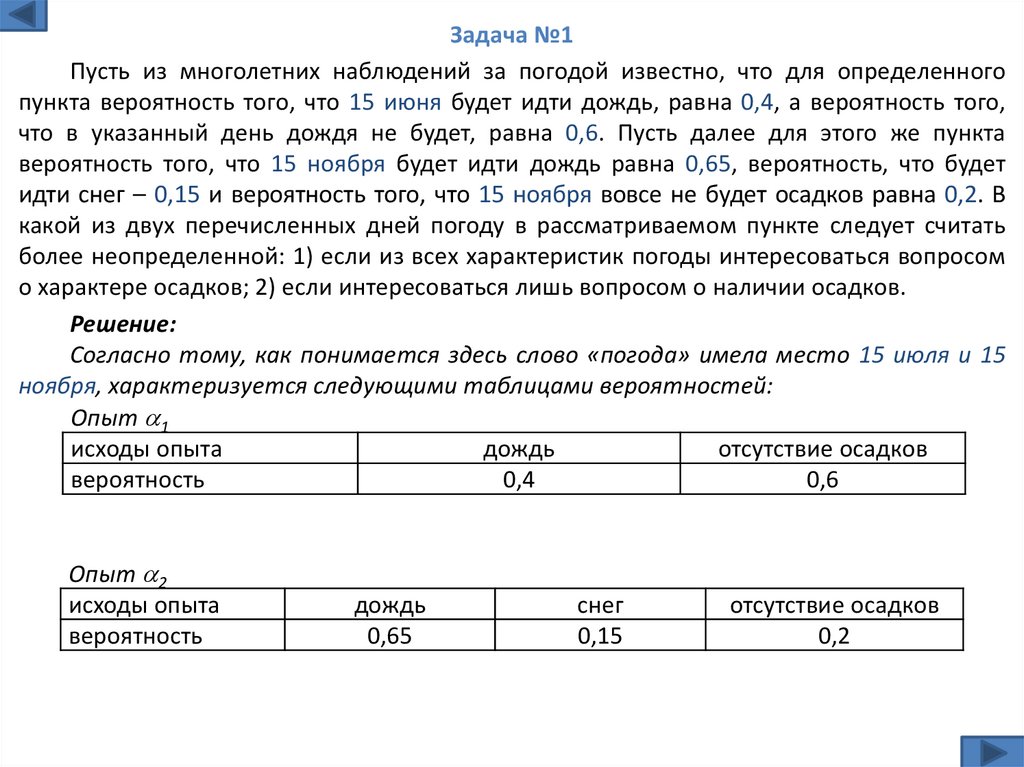
5.

Задача №1
Пусть из многолетних наблюдений за погодой известно, что для определенного
пункта вероятность того, что 15 июня будет идти дождь, равна 0,4, а вероятность того,
что в указанный день дождя не будет, равна 0,6. Пусть далее для этого же пункта
вероятность того, что 15 ноября будет идти дождь равна 0,65, вероятность, что будет
идти снег – 0,15 и вероятность того, что 15 ноября вовсе не будет осадков равна 0,2. В
какой из двух перечисленных дней погоду в рассматриваемом пункте следует считать
более неопределенной: 1) если из всех характеристик погоды интересоваться вопросом
о характере осадков; 2) если интересоваться лишь вопросом о наличии осадков.
Решение:
Согласно тому, как понимается здесь слово «погода» имела место 15 июля и 15
ноября, характеризуется следующими таблицами вероятностей:
Опыт 1
исходы опыта
дождь
отсутствие осадков
вероятность
0,4
0,6
Опыт 2
исходы опыта
вероятность
дождь
0,65
снег
0,15
отсутствие осадков
0,2

6.

1) Поэтому энтропии наших двух опытов равны
H ( 1 ) 0,4 log 0,4 0,6 log 0,6 0,4 1,33 0,6 0,74 0,98 бита
H ( 2 ) 0,65 log 0,65 0,15 log 0,15 0,2 log 0,2 0,403 0,4125 0,48 1,28 бита
Поэтому погоду 15 ноября в рассматриваемом пункте следует считать более
неопределенной, чем 15 июня.
2) Если интересоваться только тем, будут в рассматриваемый день осадки или
нет, то исходы «снег» и «дождь» опыта 2 следует объединить:
H ( 1 ) 0,98 бита (без изменений )
H ( 2 ) 0,8 log 0,8 2 log 0,2 0,264 0,48 0,72 бита
Тогда погоду 15 ноября в рассматриваемом пункте следует считать менее неопределенной, чем 15 июня.

7.

Задача №2
Имеются два дискретных троичных источника с независимыми элементами. На
выходе каждого источника появляются сообщения одинаковой длины – по 15 элементов.
Количество различных элементов в сообщении каждого источника постоянно.
Сообщения каждого источника отличаются только порядком следования элементов, а
состав сообщений постоянный. Зафиксированы два типичных сообщения:
021202120212021 – первого источника и 012101201101201 – второго. Для какого
источника неопределенность появления элементов выше?
Решение:
7
1
4
1
4
7
p12
p 22
p11
p 02
p01
p 12
15
5
15
15
15
3
Для первого источника:
2
H 1 pi1 log pi1
i 0
4
4 4
4 7
7
log log log 1,53 бит
15
15 15
15 15
15
Для второго источника:
2
H 2 pi2 log pi2
i 0
5
5 7
7 3
3
log log log 1,506 бит
15
15 15
15 15
15
Напомним, что средняя условная энтропия опыта β при условии выполнения опыта
α находится по формуле (см. лекции):
H ( ) p( A1 ) H A1 ( ) p( A2 ) H A2 ( ) ... p( Ak ) H Ak ( )

8.

Задача №3
Ракеты двух пусковых установок используются для поражения двух целей. Ракета,
пущенная с первой установки, поражает цель номер один с вероятностью 0,5, цель номер два – с вероятностью 0,3, и дает промах с вероятностью 0,2. Ракета второй установки поражает первую цель вероятностью 0,3, а вторую – с вероятностью 0,5 и вероятность промаха 0,2. Вероятность выбора первой установки 0,4. Чему равна неопределенность выбора установки: 1) если известно, что поражена вторая цель; 2) если
произошел промах?
Решение:
Полагаем, что варианты поражения целей соответствуют случайному опыту В,
а выбор ракетной установки – опыту А. Вероятности поражения целей ракетами
различных установок представляют собой условные вероятности:
PA ( B)
p A1 ( B1 )
p A2 ( B1 )
P( A) p( A1 )
p A1 ( B2 )
p A2 ( B2 )
p A1 ( B3 )
0,5 0,3 0,2
p A2 ( B3 )
0,3 0,5 0,2
p( A2 ) 0,4 0,6
Неопределенность выбора установки при условии, что поражена вторая цель
представляет собой энтропию:
2
H B 2 ( A) pB 2 ( Ai ) log( pB 2 ( Ai ))
i 1
Неопределенность выбора установки в случае промаха есть энтропия:
2
H B 3 ( A) pB 3 ( Ai ) log( pB 3 ( Ai ))
i 1

9.

Поэтому нам необходимо найти условные вероятности pB2(Ai) и pB3(Ai). Для
этого определяем элементы матрицы P(B) по формуле полной вероятности:
2
P( B j ) p ( Ai ) p Ai ( B j )
i 1
P(B1)=0,5∙0,4+0,3 ∙0,6=0,38
P(B2)=0,3∙0,4+0,5 ∙0,6=0,42
P(B3)=0,2∙0,4+0,2 ∙0,6=0,2
P( B) p( B1 )
p( B2 )
p( B3 ) 0,38 0,42 0,2

10.

Теперь мы можем найти условные вероятности (см. тему «условные вероятности»):
PAi ( B j )
PBj ( Ai )
P ( Ai )
P( B j )
PB1 ( A1 ) PB1 ( A2 )
0,526 0,474
PB ( A) PB 2 ( A1 ) PB 2 ( A2 ) 0,286 0,714
PB 3 ( A1 ) PB 3 ( A2 )
0,4
0,6

11.

В результате находим:
2
H B 2 ( A) pB 2 ( Ai ) log( pB 2 ( Ai )) 0,286 log 0,286 0,714 log 0,714 0,86
i 1
2
H B 3 ( A) pB 3 ( Ai ) log( pB 3 ( Ai )) 0,4 log 0,4 0,6 log 0,6 0,97
i 1

12.

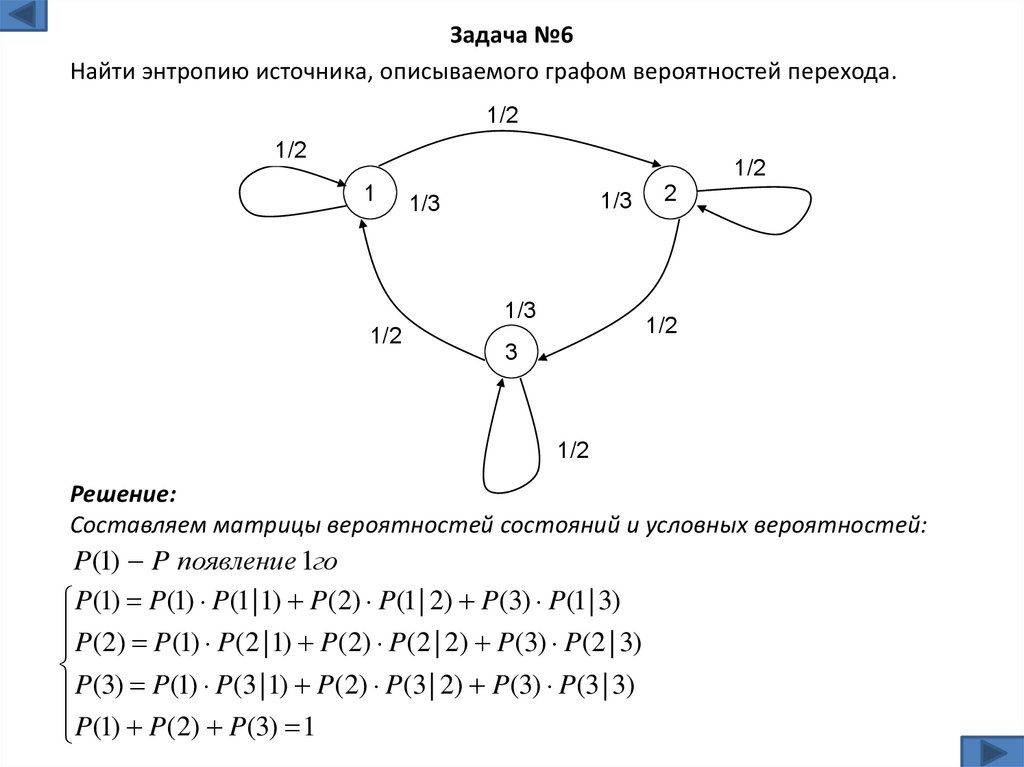
13.

Задача №6
Найти энтропию источника, описываемого графом вероятностей перехода.
1/2
1/2
1/2
1
1/3
1/3
1/3
1/2
2
1/2
3
1/2
Решение:
Составляем матрицы вероятностей состояний и условных вероятностей:
P(1) P появление 1го
P(1) P(1) P(1 | 1) P(2) P(1 | 2) P(3) P(1 | 3)
P(2) P(1) P(2 | 1) P(2) P(2 | 2) P(3) P(2 | 3)
P(3) P(1) P(3 | 1) P(2) P(3 | 2) P(3) P(3 | 3)
P(1) P(2) P(3) 1

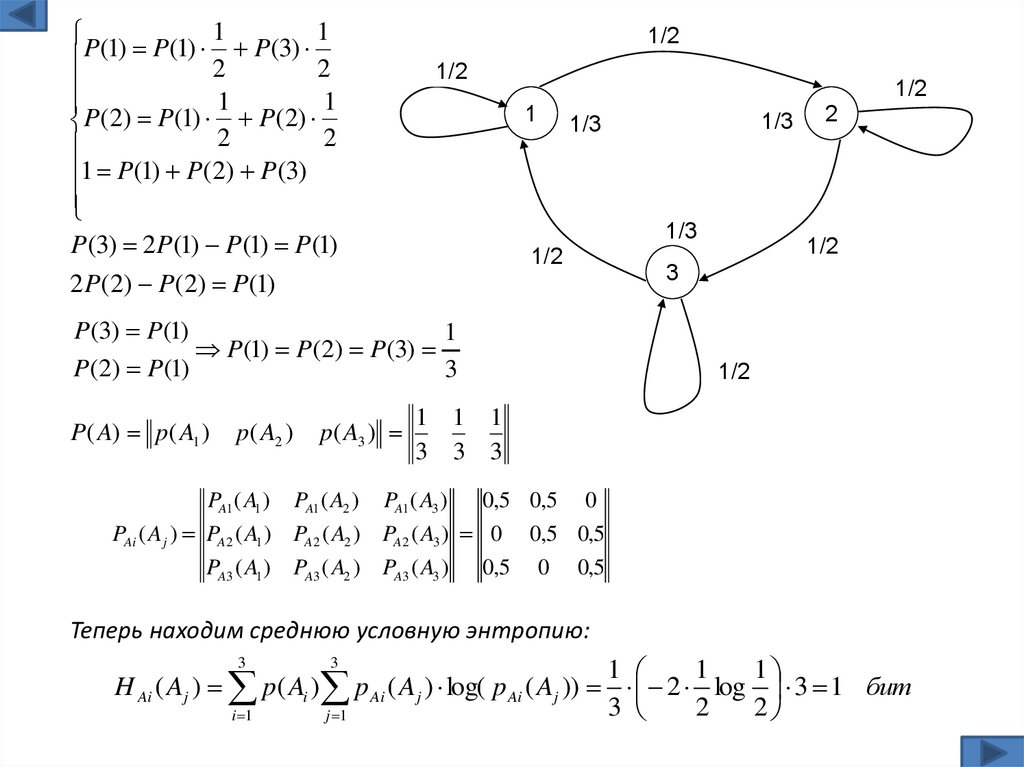
14.

1
1
P
(
1
)
P
(
1
)
P
(
3
)
2
2
1
1
P
(
2
)
P
(
1
)
P
(
2
)
2
2
1 P(1) P(2) P(3)
1/2
1/2
1/2
1
1/3
P(3) 2 P(1) P(1) P(1)
2 P(2) P(2) P(1)
1/2
P(3) P(1)
1
P (1) P(2) P (3)
P(2) P(1)
3
P( A) p( A1 )
p( A2 )
p( A3 )
1/3
1/3
2
1/2
3
1/2
1 1 1
3 3 3
PA1 ( A1 ) PA1 ( A2 ) PA1 ( A3 )
0,5 0,5 0
PAi ( Aj ) PA2 ( A1 ) PA2 ( A2 ) PA2 ( A3 ) 0 0,5 0,5
PA3 ( A1 ) PA3 ( A2 ) PA3 ( A3 )
0,5 0 0,5
Теперь находим среднюю условную энтропию:
1
1
1
H Ai ( Aj ) p( Ai ) p Ai ( Aj ) log( p Ai ( Aj )) 2 log 3 1 бит
3
2
2
i 1
j 1
3
3

15.

Задача №4
Пусть опыты α и β состоят в последовательном извлечении двух шаров из урны, содержащей m черных и (n-m) белых шаров (α - извлечение первого шара и β - извлечение
второго шара). Чему равна энтропия H(α), H(β) и условная энтропия Hα(β)?
Решение:
m
m n m
n m
H ( ) log
log
.
n
n
n
n
Обозначим:
А1 – первый раз извлекли черный шар, А2 – первый раз извлекли белый шар;
В1 – второй раз извлекли черный шар, В2 – второй раз извлекли белый шар;
Если нам известен исход опыта α, то:
m
n m
p ( A1 ) , p ( A2 )
.
n
n
m
m n m
n m
m
m
n m
H ( ) log
log
log m log n
log( n m)
n
n
n
n
n
n
n
n m
m
m
m
m
log n log m log n log( n m) log( n m) log n log n
n
n
n
n
n
m 1
n m
p A1 ( B1 )
, p A1 ( B2 )
;
n 1
n 1
m
n m 1
p A 2 ( B1 )
, p A 2 ( B2 )
.
n 1
n 1

16.

Теперь, по формуле полной вероятности
2
p( Bi ) p( A j ) p A ( Bi )
j 1
j
можно определить безусловные вероятности опыта β:
n m
m
p
(
B
)
.
p ( B1 ) ,
2
n
n
Таким образом, безусловная энтропия опыта β равна безусловной энтропии
опыта α.
Найдем частные условные энтропии опыта β, что:
m 1
m 1 n m
n m
H A1 ( )
log
log
,
n 1
n 1 n 1
n 1
m
m
n m 1
n m 1
H A2 ( )
log
log
.
n 1
n 1
n 1
n 1
m
n m
H ( ) H A1 ( )
H A2 ( )
n
n
И, наконец, находим:
m m 1
m 1
n m
n m
H ( ) p( A1 ) H A1 ( ) p( A2 ) H A2 ( )
log
log
n n 1
n 1
n 1
n 1
n m m
m
n m 1
n m 1 nm m 2 n 2 2nm m 2 n m
log
log
n n 1
n 1
n 1
n 1
n(n 1)
nm n 2 n m m(1 n) n(n 1) n m
n(n 1)
n(n 1)
n

17.

Задача №7
Определить максимальную энтропию телевизионного изображения, содержащего
500 строк по 650 элементов в строке, при условии, что яркость каждого элемента передается восьмью квантованными уровнями, если: а) уровни не коррелированы; б) статистическая связь между различными градациями яркости задана графом
1/3
1/2
1/3
1
1/3
2
1/2
1/3
1/3
1/3
1/3
3
1/3
1/3
4
1/3
5
1/3
1/3
1/3
1/3
1/3
6
1/3
1/2
1/2
7
1/3
8
1/3
Решение:
а) Максимальная энтропия одного элемента изображения, при условии, что уровни не коррелированы, составляет (энтропия максимальна в случае, если уровни являются равновероятными):
1
p(i) , i 1...8
H 1 log( 8) 3 бита
500 650 = 3250000
8
Так как, у нас элементов 500х650, то возможное количество состояний 8500 650
изображения , а максимальная энтропия телевизионного изображения равна:
H И log( 8500 650 ) 500 650 log( 8) 325000 H 1 975000 бит

18.

б) Найдем максимальную среднюю условную энтропию одного элемента. Для
этого, исходя из приведенного графа, составим матрицу условных переходных вероятностей:
0,5 0,5 0 0 0 0 0
0
1
3
0
PAi ( A j )
1
3
1
3
1
3
1
3
1
3
0
1
3
1
3
1
3
0
0
0
0
0
0
0
0
0
0
0
1
3
1
3
1
3
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
3
1 1
0
3 3
1 1
1
3 3
3
0 0,5 0,5
Уровни считаем равновероятными, так как ищем максимальную энтропию, значит:
P( Ai ) 0,125 0,125 0,125 0,125 0,125 0,125 0,125 0,125
Теперь находим максимальную среднюю условную энтропию одного элемента
8
8
изображения:
1
H Ai ( A j ) p( Ai ) p Ai ( A j ) log( p Ai ( A j )) 1,439 бит
i 1
j 1
Отсюда максимальная энтропия телевизионного изображения равна:
H И 500 650 H 1Ai ( A j ) 467600 бит

19.

Задача №8
Дана матрица вероятностей
совместных событий:
Определить энтропии:
H(X), H(Y), Hy1(X), Hx2 (Y), HX (Y), HY(X), H(X, Y).
X
Решение:
18 18 18
p( x1 y1 )
P( X , Y )
Y 18 0 18
p( x2 y1 )
18 18 18
p( x3 y1 )
P( X , Y )
p( x1 y 2 )
p ( x2 y 2 )
p ( x3 y 2 )
X
18 18 18
18 0 18
18 18 18
Y
p( x1 y3 )
p ( x2 y3 )
p ( x3 y 3 )
1) По формуле полной вероятности имеем:
p( xi ) p( y1 xi ) p( y2 xi ) p( y3 xi ), i 1...3; p( y j ) p( y j x1 ) p( y j x2 ) p( y j x3 ), j 1...3
3
2
3
2
3
p( xi ) , i 1...3; p( x2 ) ; p( y1 ) , p( y2 ) , p( y3 ) ;
8
8
8
8
8
3
2 6
1
3 3 2
H ( x) p( xi ) log p( xi ) 2 log log 1,4 2 1,05 0,5 1,55 бит
8 8
4
i 1
8 8 8
3
2 6
1
3 3 2
H ( y ) p( yi ) log p( yi ) 2 log log 1,4 2 1,05 0,5 1,55 бит
8 8
4
i 1
8 8 8
3
3
p( xi ) p( y j , xi ), p( yi ) p( x j , yi ), H ( x) H ( y) 1,55 бита.
j 1
2)
3
3
i 1
j 1
j 1
3
3
i 1
j 1
H y ( x) p( yi ) p yi ( x j ) log( p yi ( x j )), H x ( y) p( xi ) pxi ( y j ) log( pxi ( y j )),
p yi ( x j ) p( yi , x j ) p( yi ) , p xi ( y j ) p( xi , y j ) p( xi ) , H y ( x) H x ( y ) 1,43 бита .

20.

3
3)
H y1 ( x) p y1 ( x j ) log( p y1 ( x j )),
j 1
3
H x 2 ( y) px 2 ( y j ) log( px 2 ( y j )),
j 1
1
1,58 бита .
3
1 8 1
1 8 1
1 8 1
p y1 ( x1 ) , p y1 ( x2 ) , p y1 ( x3 ) ,
8 3 3
8 3 3
8 3 3
1
1
H x 2 ( y ) 2 log 1 бит .
2
2
1 8 1
1 8 1
p x 2 ( y1 ) , p x 2 ( y2 ) 0, p x 2 ( y3 ) .
8 2 2
8 2 2
H y1 ( x) log
3
4)
1 8 1
p y 2 ( x1 ) ,
8 2 2
3
H ( x, y) p( xi , y j ) log p( xi , y j ) или H ( x, y) H ( x) H x ( y);
i 1 j 1
p yi ( xi )
H y 2 ( x ) 1, H y 3 ( x) 1,59
3
1 1 1
3 3 3
1
1
0
2
2
1 1 1
3 3 3
p xi ( y j )
1
3
1
2
1
3
1 1
3 3
1
0
2
1 1
3 3
3
2
H y ( x) H x ( y) 1,44
H y ( x) p( yi ) H yi ( x) 2 1,59 1,44
8
8
i 1 3
3
1
1
H ( x, y) p( xi , y j ) log p( xi , y j ) 8 log 3 бита .
8
8
i 1 j 1

21.

Задача №9
Информация передается при помощи частотно-модулированных сигналов, рабочая
частота F которых изменяется с равной вероятностью в пределах от F1=10МГц до
F2=50МГц. Определить энтропию значения частоты, если точность измерения частоты
F=2кГц.
Решение:
Так как точность измерений составляет F=2кГц, то мы имеем дело с
n
F2 F1
20 10 3 числом равновероятных исходов.
F
1
p( Fi )
20 10 3
Поэтому энтропия частоты будет определяться:
H ( F ) log n 14,28 бит.

22.

Напомним некоторые свойства энтропии источников информации.
1) Условная энтропия источника всегда меньше безусловной:
0 H (X | Y) H (X )
2) Если составной источник состоит из источников информации X и Y, то для случая
независимых источников:
H ( X , Y ) H ( X ) H (Y ),
а для случая зависимых друг от друга источников:
H ( X , Y ) H ( X ) H (Y | X ) или
H ( X , Y ) H (Y ) H ( X | Y ).
Задача №11
Элементы алфавитов X и Y статистически связаны. Известно, что H(X) = 8 бит, H(Y) =
12 бит. В каких пределах меняется условная энтропия H(Y | X) при изменении H(X | Y) в
максимально возможных пределах?
Решение:
Т.к.: H(X, Y) = H(X) + H(Y | X) и H(X, Y) = H(Y) + H(X | Y), то можем записать:
H(X) + H(Y | X) = H(Y) + H(X | Y).
Условная энтропия может изменяться: 0 H(X | Y) H(X), поэтому значения
какие будет принимать H(Y | X) при изменении H(X | Y) можно определить:
H(Y | X) = H(Y) + H(X | Y) - H(X).
При минимальном значении: H(X | Y) = 0: H(Y | X) = 0 + 4 = 4 бит.
При максимальном значении: H(X | Y) = H(X) = 8: H(Y | X) = 8 + 4 = 12 бит.
4 H (Y | X ) 12.

23.

Дополнительные задачи
Задача №13
Имеются два дискретных источника информации, заданных следующими таблицами вероятностей:
Х
х1
х2
Y
y1
y2
y3
вероятность р1
р2
вероятность q1
q2
q3
Определить, какой источник обладает большей неопределенностью в случае, если:
а) p1 = p2, q1 = q2 = q3 ; б) p1 = q1 , p2 = q2 + q3 .
Решение:
1) В случае равновероятных элементов большей неопределенностью обладает
троичный источник. При этом неопределенность может быть подсчитана, как logM,
где М – число равновероятных состояний.
2) Запишем:
H ( X ) p1 log p1 p2 log p2 q1 log q1 (q2 q3 ) log( q2 q3 )
q1 log q1 q2 log( q2 q3 ) q3 log( q2 q3 )
1
1
1
q1 log q2 log
q3 log
q1
(q2 q3 )
(q2 q3 )
1
1
1
H (Y ) q1 log q1 q2 log q2 q3 log q2 q1 log q2 log q3 log
q1
q2
q3
Отсюда следует, что H ( X ) H (Y ).

24.

Задача №14
Определить среднюю неопределенность появления одного символа сообщения
01001000101001, при условии, что вероятность появления элементов на выходе источника информации с течением времени не изменяется, а приведенная последовательность символов – типичная.
Решение:
5
5 9
9
H ( x) log log
0,94.
14
14 14
14
Задача №15
Измерительное устройство регистрирует временные интервалы, распределенные
случайным образом в пределах от 100 до 500мс. Как изменится энтропия случайной
величины при изменении точности измерения с 1мс до 1мкс?
Решение:
При точности измерения 1мс случайная величина принимает (500-100)/1=400
равновероятных значений, а значит ее энтропия:
H 1 ( x) log( 400) 8,64 бит
А при точности измерения 1мкс случайная величина принимает
(500-100)/0.001=400000 равновероятных значений, а значит ее энтропия:
H 1 ( x) log( 400000) 18,61 бит .
Значит, энтропия случайной величины увеличится примерно на 10 бит.

25.

Задача №16
Опыт Х – случайный выбор целого числа от 1 до 1050. Опыт Y – определение величин остатков от деления этого числа на 35. Определить энтропии H(X), H(Y), H(X | Y).
Решение:
Чтобы найти энтропии H(X), H(Y), строим вероятностные схемы для X и Y.
Т.к. Х может принимать равновероятные значения от 1 до 1050, то получаем:
x1
x2 ... xi ... x1050
X
,
1 1050 1 1050 ... 1 1050 ... 1 1050
т.к. при делении на 35, остаток от деления может принимать 35 равновероятных значений от 0 до 34, а значит:
y
y2 ... yi ... y35
Y 1
.
1 35 1 35 ... 1 35 ... 1 35
Находим: H ( X ) log 1050 10,02 бит , H (Y ) log 35 5,12 бит .
Для определения H(X | Y) построим матрицу P(X | Y). При построении данной
матрицы будем исходить из следующих соображений, если мы имеем остаток от
деления на 35 y1 = 0, то этому должны отвечать числа x35 =35, x70 =70,…, x1050 =1050,
которые отстоят друг от друга на 35 и количество этих чисел равно 1050/35=30. Так
как числа равновероятные, то вероятности их появления при условии, что остаток
от деления равен 0, составляет 1/30. Тоже самое относится к значениям Х при
условии других остатков от деления. Т.о. получаем:

26.

x1
x2
x3 ... x35 x36 x37 ... x1050
y1 1 / 30 0
0 ... 0 1 / 30 0 ... 0
0 1 / 30 ... 0
P( X | Y ) y2 0 1 / 30 0 ... 0
y3 0
0 1 / 30 ... 0
0
0 ... 0
...
...
... ... ...
...
... ... ...
y35 0
0
0 0 1 / 30 0
0 0 1 / 30
Находим:
35
1050
i 1
j 1
H ( X | Y ) p( yi ) p( x j | yi ) log( p( x j | yi )) log 30 4,9 бита .