Исследование одной геометрической задачи

1.

Исследование одной
геометрической задачи.
Найдёшкина Л.А.,
учитель математики
МБОУ «Сапоговская СОШ»
20178г

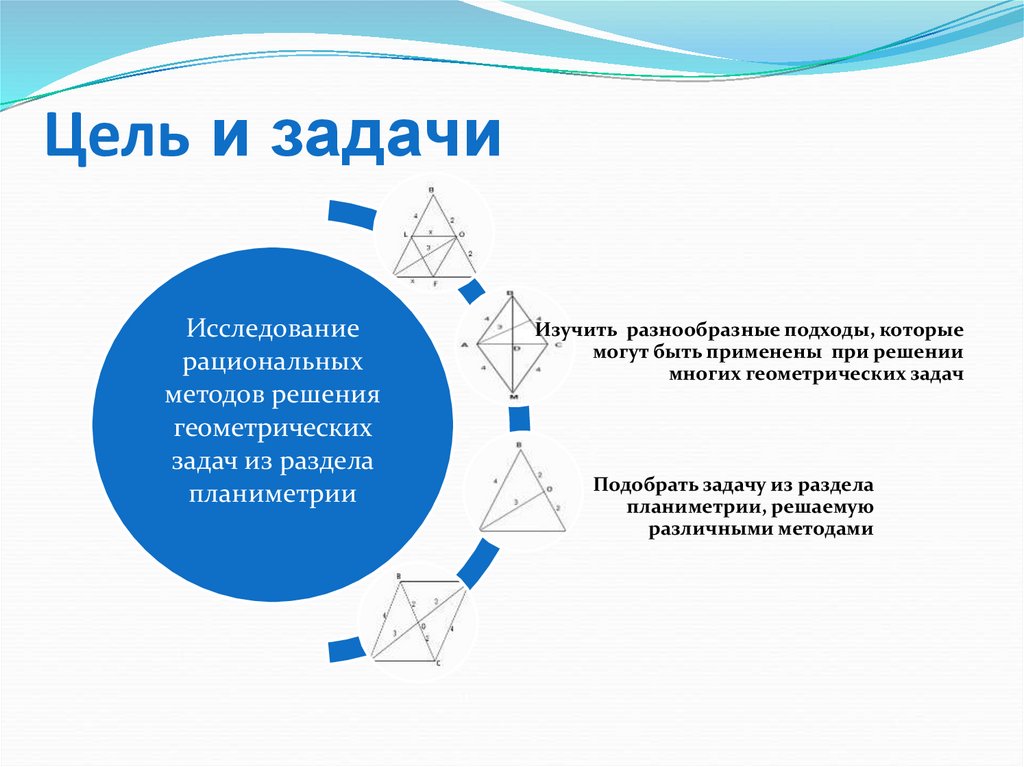
2. Цель и задачи

Исследование
рациональных
методов решения
геометрических
задач из раздела
планиметрии
Изучить разнообразные подходы, которые
могут быть применены при решении
многих геометрических задач
Подобрать задачу из раздела
планиметрии, решаемую
различными методами

3. Актуальность

Геометрия является самым могущественным средством для
изощрения наших умственных способностей и дает нам возможность
правильно мыслить и рассуждать.
Г.Галилей
Большинство задач по планиметрии не решается с
помощью жестких алгоритмов, почти каждая
геометрическая задача требует своего подхода. Здесь
уже мало иметь те или иные знания, нужно уметь
применять их в каждом конкретном случае. Особое
значение имеет выработка разнообразных
эвристических подходов, которые могут быть успешно
применены при решении многих геометрических
задач.
Задача выступила не только в качестве иллюстрации
теории, но и рассматривалась как самостоятельный
объект, как средство развития исследовательской и
эвристической деятельности.

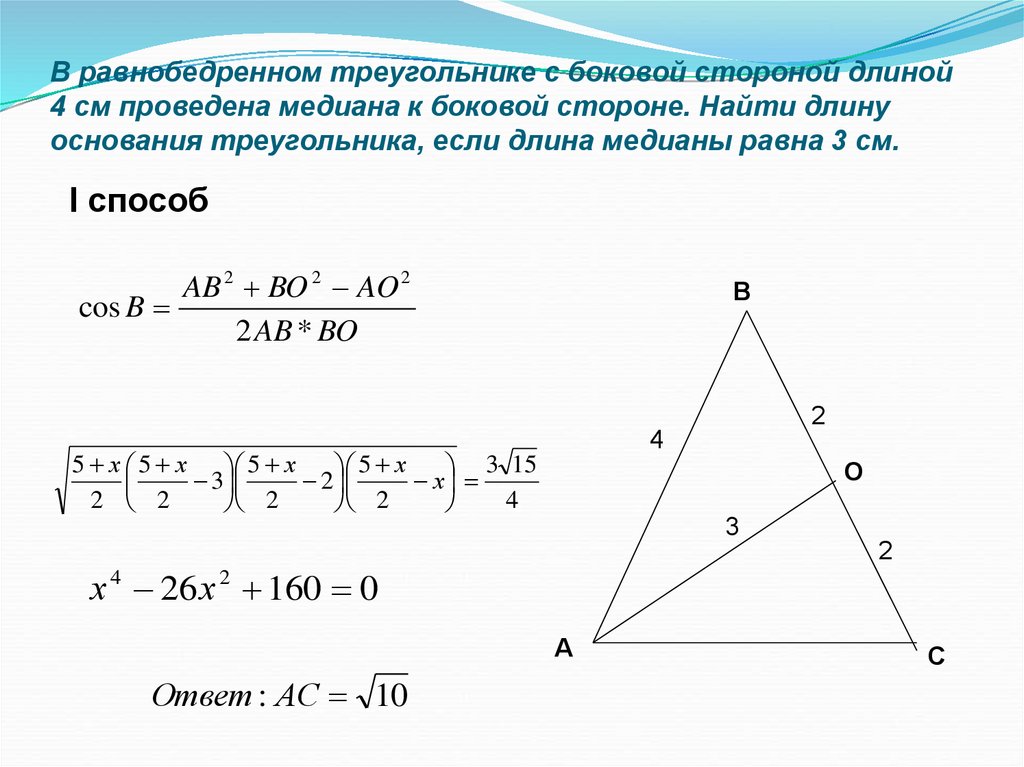
4. В равнобедренном треугольнике с боковой стороной длиной 4 см проведена медиана к боковой стороне. Найти длину основания

треугольника, если длина медианы равна 3 см.
I способ
AB 2 BO 2 AO 2
cos B
2 AB * BO
В
2
4
5 х 5 х
5 х
5 х
3 15
3
2
х
2 2
4
2
2
О
3
2
х 4 26 х 2 160 0
А
Ответ : АС 10
С

5.

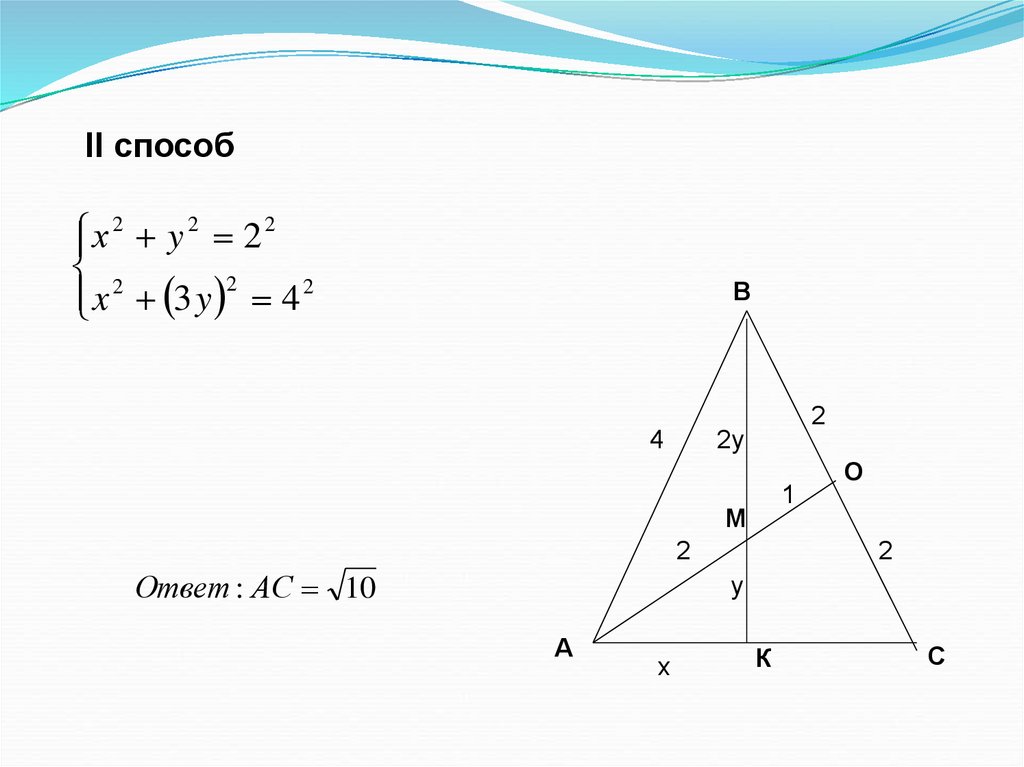
II способ
х 2 y 2 2 2
2
x 3 y 2 4 2
В
2
4
2y
1
М
2
Ответ : АС 10
О
2
y
А
х
К
С

6.

III способ
В
OL2 9 3 x 2
2
OL 4 x 2
2
4
О
3
2
Ответ : АС 10
А
х
3х
L
С

7.

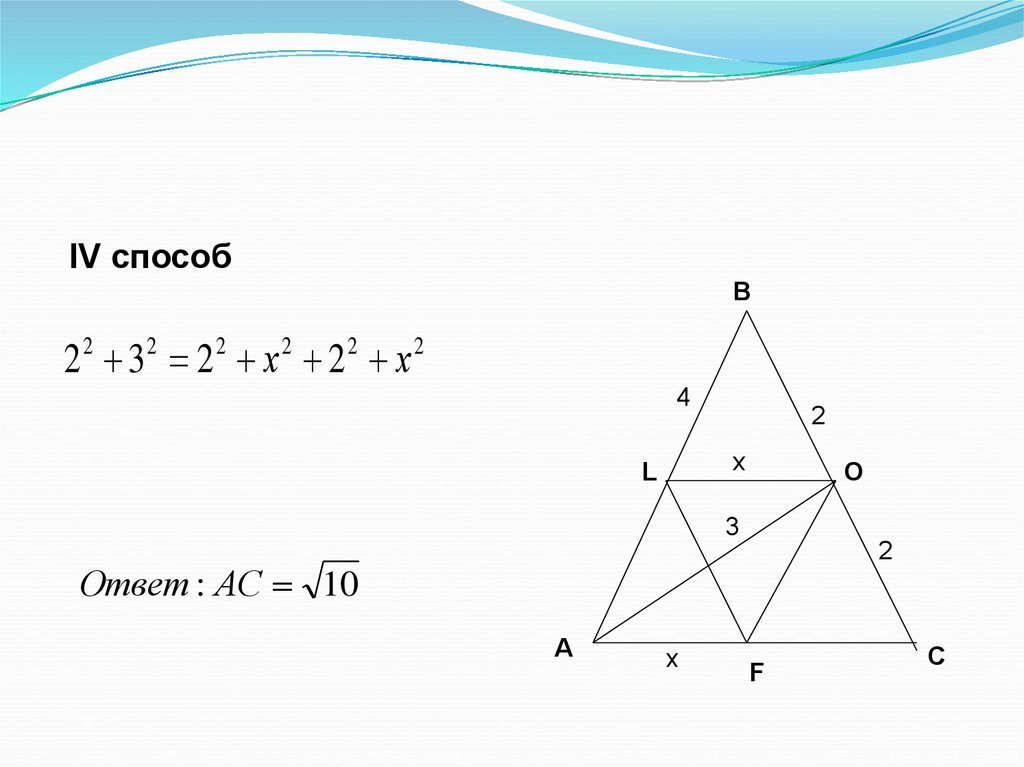
IV способ
В
2 2 32 2 2 х 2 2 2 х 2
4
2
x
L
О
3
2
Ответ : АС 10
А
x
F
С

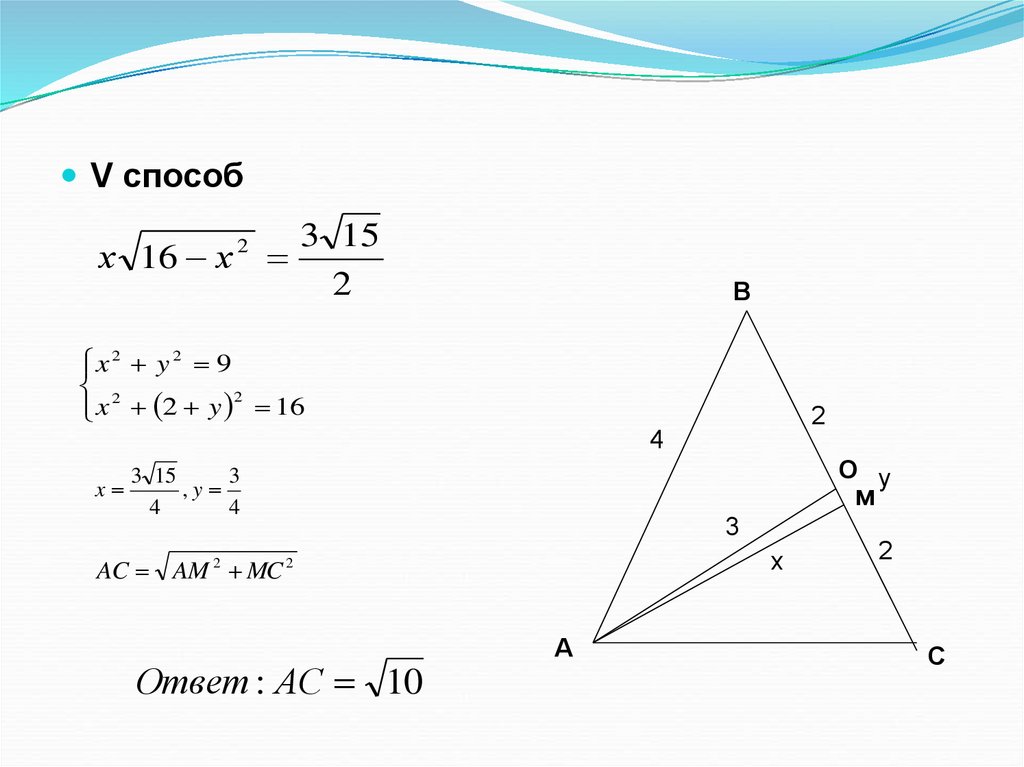
8.

V способ
3 15
х 16 х
2
2
В
2
2
x y 9
2
2
x 2 y 16
2
4
x
О y
3 15
3
,y
4
4
м
3
х
AC AM 2 MC 2
Ответ : АС 10
А
2
С

9.

VI способ
В
D
3
2
4 6 4 х 4 х
2
4
О
3
А
2
2
2
2
4
2
С
Ответ : АС 10
2

10.

В
VII способ
ВМ АС 4 4 4 4
2
2
2
ВМ - ?
2
2
4
2
4
3
А
С
D
4
4
М

11. Вывод

Невозможно указать два, три и даже пять методов,
освоив которые, научился бы решать все геометрические
задачи. Они всегда непредсказуемы. В этом сложность
геометрических задач, их отличие от большинства
школьных алгебраических задач. Но в этом заключается и их
прелесть. Каждая геометрическая задача требует
индивидуального подхода, определенной доли
изобретательности и интуиции. Конечно же, для решения
таких задач необходимо твердо знать теоремы школьного
курса. Но этого мало. Нужно уметь применять эти теоремы,
и каждый раз в новой ситуации. Такое умение приобретается
с опытом решения задач. Именно эти знания и этот опыт
служат базой, на которую опираются и интуиция, и
изобретательность.

12.

Благодарю за внимание!