Геометрические задачи на экстриемум

1.

2.

I.
II.
III.
IV.
V.
Оглавление
Введение
------------------------------------------------ с.1
а) История развития задач на экстремумы ---------- с.2 – с.4
б) Экстремумы функции --------------------------------- с.5 – с.6
в) Задачи на экстремумы --------------------------------- с.7 - с.11
Заключение ------------------------------------------------- с.12
Список использованной литературы ------------------- с.13
Приложение ------------------------------------------------- с. 14-16

3.

Цель: исследовать решение геометрических задач на
экстремумы.
Для достижения этой цели были поставлены следующие
задачи:
1. Подобрать и изучить дополнительную литературу по теме
2. Изучить методы решения геометрических задач на
экстремумы и грамотно переводить на математический
язык
3. Научиться решать экстремальные задачи
Объект исследования: задачи на экстремум
Предмет исследования: решение геометрических задач на
экстремум
Практическая значимость работы: 1. задачи с национально региональным компонентом могут быть применены
учителями на уроках математики
2. Задачи на экстремум имеют широкий спектр применения во
всех областях человеческой жизни

4.

«В мире не происходит ничего, в чем бы
не был виден смысл какого- нибудь
максимума или минимума»
Леонард Эйлер (1707 – 1783 г.г.)

5.

Задачи, где требуется определить условия, при которых некоторая
величина принимает наибольшее и наименьшее значение, принято
называть задачами «на экстремум» ( от латинского слова
«extremum» - «крайний») или задачами на «максимум» и
«минимум» (от латинских «maximum» и «minimum» соответственно «наибольшее» и «наименьшее»). Такие задачи
часто встречаются в технике и естествознании, в повседневной
деятельности людей.
Самая простая и, вероятно, самая древняя геометрическая задача на
экстремум такая: какой из всех прямоугольников заданного
периметра имеет наибольшую площадь? Решение ее было известно
древнегреческой математике. Оно изложено в vɪ книге «Начал»
Евклида (книга «Начала» древнегреческого ученого Евклида
относится к 3 веку до нашей эры), где доказывается, что если
рассмотреть прямоугольник и квадрат одного и того же периметра,
то площадь квадрата будет больше. Я исследовал эту задачу и
решение покажу в 2 части своей работы (задача 1).

6.

Рассмотренная задача относится к широкому классу
геометрических задач на экстремум – так называемым
изопериметрическим задачам, в которых фигура с экстремальным
свойством отыскивается среди других с равным периметром.
Изопериметрические задачи объединяют также одним названием
– «задачи Дидоны». Они названы так по имени легендарной
основательницы города Карфагена и его первой царицы.
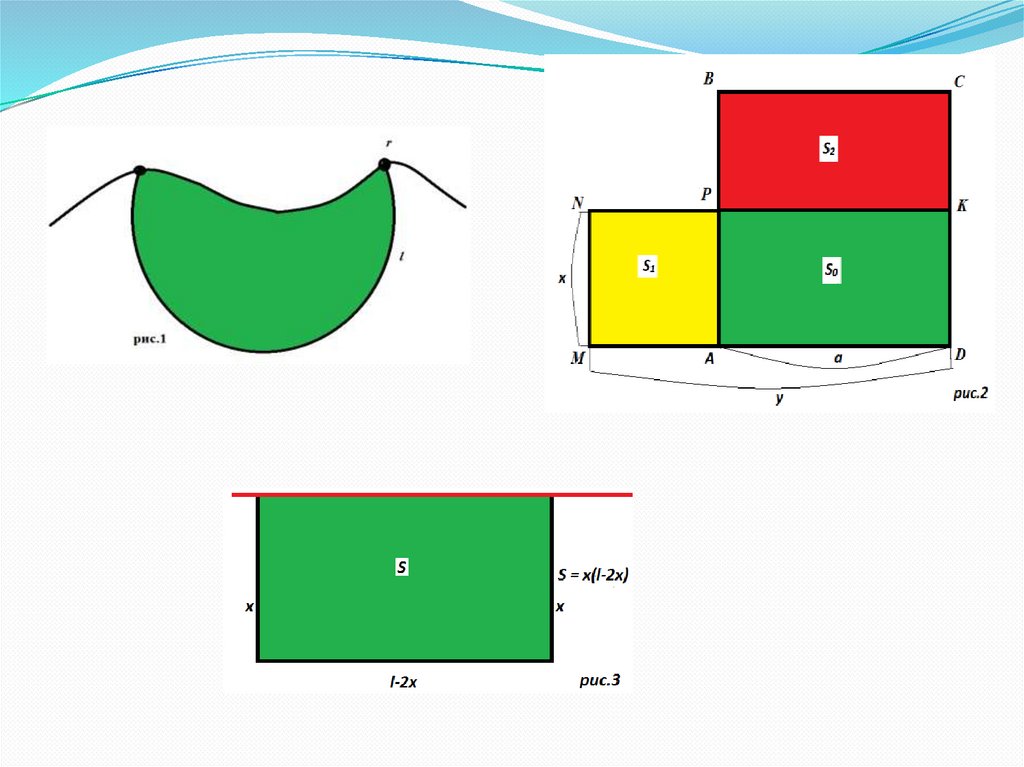
Если учесть, что Дидона выбирала участок, примыкающий к
берегу моря, то математическую задачу, с которой она столкнулась,
можно сформулировать так: какой формы должна быть кривая
длины , чтобы площадь фигуры, ограниченная этой кривой и
заданной линией r, была наибольшей? (рис.1)

7.

Задача 1. Какой из всех прямоугольников заданного
периметра имеет наибольшую площадь?
Я хочу показать доказательство самой древней
задачи на экстремум, которое основано на
сравнении площадей (рис.2).

8.

Задача 2 (частный случай задачи Дидоны).
Дидона выбрала участок, примыкающий
большей стороной к берегу моря, если
береговая линия не кривая, а прямая длины l.
При каких значениях l площадь
ограничиваемого участка будет наибольшей?
Решение:
Эту задачу я решил по изложенной схеме:
1. Формализация (перевод на язык математики)
2. Решение полученной задачи:
3. Интерпретация найденного решения

9.

Задача 3. Из квадратного листа жести со стороной
а надо изготовить открытую сверху коробку,
вырезав по углам (рис.5, рис.6) квадратики и
загнув образовавшиеся кромки. Какой должна
быть сторона основания коробки, чтобы ее объем
был максимальным?
Решение:
1. Формализация.
2. Решение полученной задачи:
3. Максимальный объем имеет та коробка,
сторона основания которой равен 2 а /3 .

10.

Я составил подобные задачи на экстремумы с
национально – региональным компонентом.
Задача 4.
Вышка (точка В) сотовой связи оператора «Мегафон»
расположена в поле на расстоянии 1 км от ближайшей
точки шоссе Верхняя Иволга – Иволга (точка А). С
вышки нужно велосипедисту доехать до Иволгинского
дацана (точка Д), расположенного по шоссе в 4 км от
упомянутой точки (считаем шоссе прямолинейным).
Скорость велосипедиста по полю 4 км/ч, а по шоссе 5
км/ч. К какой точке шоссе ему надо ехать, чтобы в
кратчайшее время достичь Дацана? (рис.7)
Решение:
В – вышка. Д – Иволгинский дацан, ВСД – маршрут
следования велосипедиста
АВ = 1 км
АД = 4 км
Пусть АС = х, где 0 ≤ х ≤ 4

11.

Задача 5.
Лодка находится на Карасином озере на расстоянии 3
км от ближайшей точки А берега. Ребята, которые
катались на этой лодке, желают достигнуть лагеря
«Черемушки», находящегося на берегу на расстоянии 5
км от А (участок АВ берега считаем прямолинейным).
Лодка движется со скоростью 4 км/ч, а ребята, выйдя из
лодки,
могут в час пройти 5 км. К какому пункту берега
должна пристать лодка, чтобы ребята достигли лагеря в
кратчайший срок? (рис.8)
Решение:
Л – лодка, Ч – лагерь «Черемушки»
ЛА = 3 км
АЧ = 5 км
Пусть АВ = х, где 0 ≤ х ≤ 5
Ответ: Лодка должна пристать к пункту В, удаленному
от лагеря «Черемушки» на расстоянии 1 км.

12.

13.