Similar presentations:
Математический пакет MathCAD
1.
Математическийпакет
MathCAD
2.
MathCAD - это интегрированная системапрограммирования, ориентированная на проведение
математических и инженерно-технических расчетов.
В состав среды MathCAD входят несколько
интегрированных между собой компонентов:
• редактор для ввода и редактирования текста и
формул;
• вычислительный процессор, предназначенный для
проведения расчетов согласно введенным формулам;
• символьный процессор, обладающий
возможностями системы искусственного
интеллекта;
• графический процессор.
2
3.
Основными достоинствами пакета являются:• легкость и наглядность программирования задач;
• запись сложных математических выражений в том
виде, в котором они обычно записываются инженерами
на бумаге;
• простота в использовании;
• возможность создания встроенными средствами
качественных отчетов с таблицами, графиками,
текстом.
3
4.
Документ MathCAD — это в полном смысле этогослова компьютерная программа, а сама система
MathCAD — настоящая система программирования.
Большинство других сред программирования (таких как
Си, Фортран, Бейсик и т. п.) разделяют редактирование
кода программ и их выполнение. В MathCAD и код
программы, и результат их выполнения объединены в
одном документе. Тем не менее, редактирование формул
и их расчеты выполняются раздельно, и пользователь
может управлять опциями вычислений.
4
5.
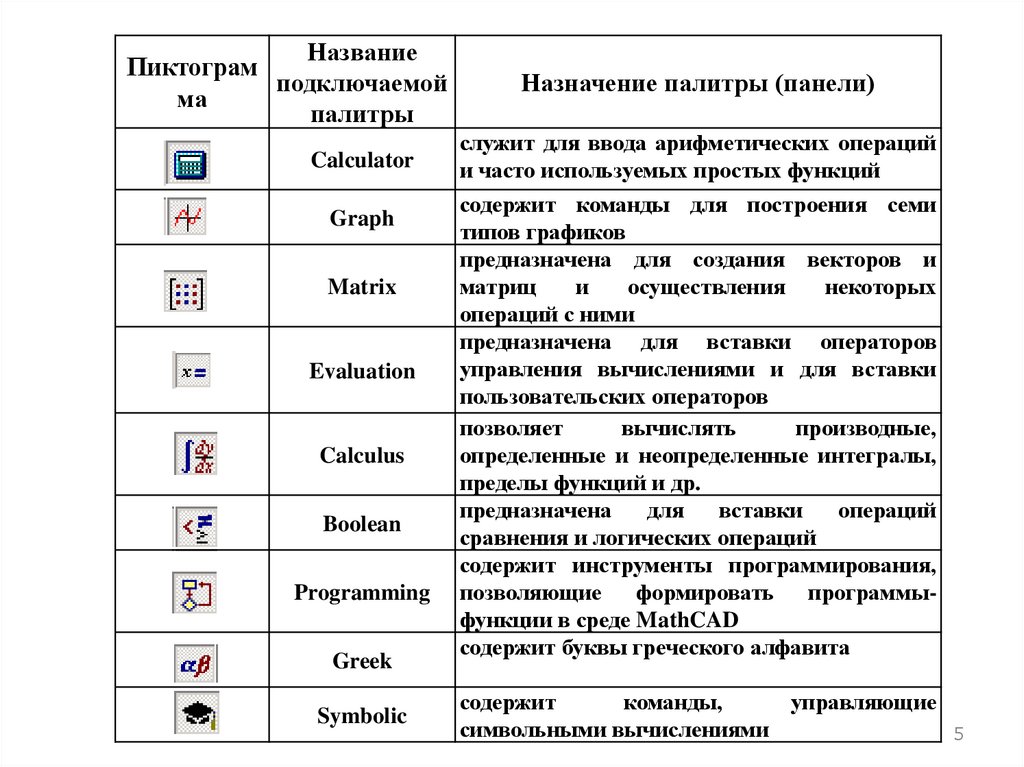
НазваниеПиктограм
подключаемой
ма
палитры
Calculator
Graph
Matrix
Evaluation
Calculus
Boolean
Programming
Greek
Symbolic
Назначение палитры (панели)
служит для ввода арифметических операций
и часто используемых простых функций
содержит команды для построения семи
типов графиков
предназначена для создания векторов и
матриц
и
осуществления
некоторых
операций с ними
предназначена для вставки операторов
управления вычислениями и для вставки
пользовательских операторов
позволяет
вычислять
производные,
определенные и неопределенные интегралы,
пределы функций и др.
предназначена
для
вставки
операций
сравнения и логических операций
содержит инструменты программирования,
позволяющие
формировать программыфункции в среде MathCAD
содержит буквы греческого алфавита
содержит
команды,
управляющие
символьными вычислениями
5
6.
Замечание: необходимо учитывать, что компиляторсреды MathCAD прочитывает содержимое рабочей области
два раза – слева направо и сверху вниз. В этой связи
вычислительные блоки должны располагаться с учетом их
приоритетности.
6
7.
Структура MathCAD-документаВ документе MathCAD могут размещаться области трех типов:
1) текстовая;
- неисполняемая область
2) вычислительная;
- исполняемые области
3) графическая.
7
8.
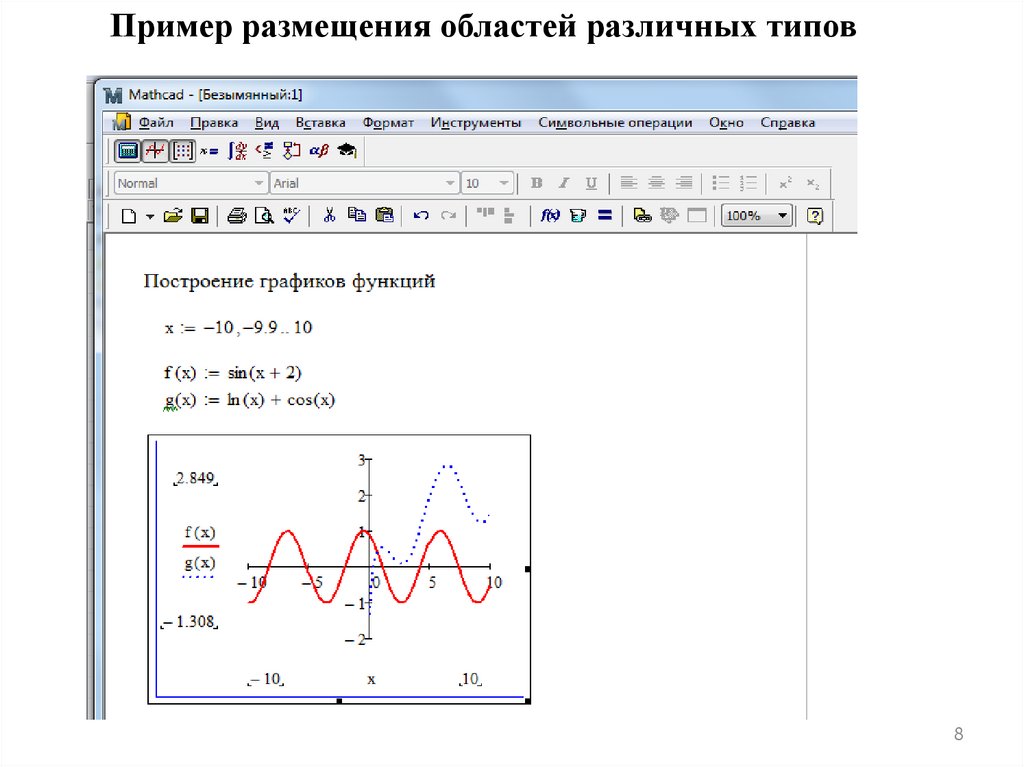
Пример размещения областей различных типов8
9.
Из символов алфавита формируются идентификаторы(имена) переменных и функций.
Синтаксис при определении имен переменных и функций имеет
следующие ограничения:
строчные и прописные буквы считаются различными символами,
поскольку в системе MathCAD имеет место понятие
«чувствительность к регистру»;
дробная часть в числах пишется через точку;
различные значения пишутся через запятую;
имена не могут совпадать с именами встроенных функций,
констант и размерностей, поскольку это приведет к их
переопределению;
имена переменных и функций не различаются в документе, т.е.
если сначала определить функцию f(x), а потом переменную f, то в
оставшейся части документа будет утерян доступ к функции f(x),
поскольку произойдет ее переопределение.
9
10.
К основным объектам входного языка системы MathCADотносятся:
константы;
переменные;
операторы;
функции.
Замечание: данные объекты входного языка
участвуют в образовании вычислительных областей
документа MathCAD.
10
11.
Константами называются поименованные объекты,хранящие некоторые значения, которые не могут быть
изменены.
В MathCAD применяются десятичные, восьмеричные и
шестнадцатеричные числовые константы. Десятичные
константы могут быть целочисленными, вещественными,
заданными с фиксированной точкой, и вещественными,
заданными в виде мантиссы и порядка. В MathCAD
содержится особый вид констант - размерные. Помимо
своего числового значения они характеризуются еще и
указанием на то, к какой физической величине они
относятся. Для этого указания используется символ
умножения. В системе MathCAD заданы следующие
основные типы физических величин: time (время), length
(длина), mass (масса) и charge (заряд). При необходимости
их можно изменить на другие.
11
12.
Переменная – именованный объект данных, имеющийнекоторое значение, которое может изменяться по ходу
выполнения программы. Значения переменным задаются с
помощью знака присвоить .
Переменные, определяемые в документе MathCAD, могут
быть:
1) системные;
2) пользовательские (далее просто переменные).
Системная переменная – это переменная, созданная
разработчиками
среды
MathCAD,
имеющая
предопределенное системой начальное значение.
Пользовательская переменная определяется самим
пользователем в целях решения конкретной задачи путем
назначения ей идентификатора в соответствии с синтаксисом
определения имен и указания значения этой переменной.
12
13.
Переменная в системе MathCAD может приниматьзначения следующих типов:
число;
массив;
текст (строка).
Среда MathCAD оперирует с вещественными,
комплексными числами, а также встроенными
константами. Любое выражение, начинающееся с
цифры, интерпретируется как число.
13
14.
Массив — имеющая уникальное имя совокупностьконечного числа числовых или символьных элементов,
упорядоченных
некоторым
образом
и
имеющих
определенные адреса.
В пакете MathCAD используются массивы двух
наиболее распространенных типов:
– одномерные (векторы);
– двухмерные (матрицы).
Вывести шаблон матрицы или вектора можно одним
из способов:
выбрать пункт меню Вставка — Матрица;
нажать комбинацию клавиш Ctrl + M;
нажать кнопку
на Панели векторов и матриц.
14
15.
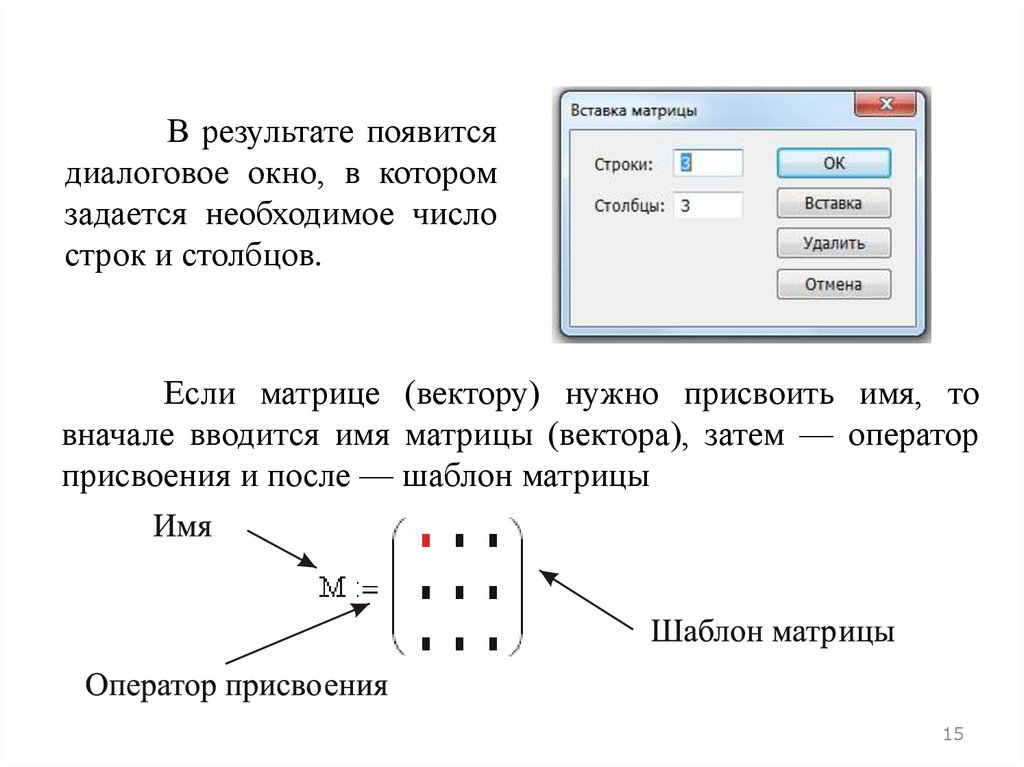
В результате появитсядиалоговое окно, в котором
задается необходимое число
строк и столбцов.
Если матрице (вектору) нужно присвоить имя, то
вначале вводится имя матрицы (вектора), затем — оператор
присвоения и после — шаблон матрицы
15
16.
Ранжированные (дискретные) переменныеРанжированная переменная – переменная, которая
принимает ряд значений при каждом ее использовании.
Для определения ранжированной переменной общего
вида используется выражение:
Имя_переменной := начальное_значение, начальное_значение +
шаг .. конечное_значение
Пример:
Если шаг равен 1, тогда ранжированную переменную можно
задавать следующим образом:
Имя_переменной := начальное_значение .. конечное_значение
Пример:
Любое выражение с ранжированными переменными после
знака равенства (=) создает таблицу вывода
16
17.
Любое выражение с ранжированными переменнымипосле знака равенства (=) создает таблицу вывода
17
18.
Операторы — элементы MathCAD, с помощьюкоторых можно создавать математические выражения. К ним,
например, относятся символы арифметических операций,
знаки вычисления сумм, произведений, производной,
интеграла и т.д.
Оператор определяет:
а) действие, которое должно выполняться при наличии тех или
иных значений операндов;
б) сколько, где и какие операнды должны быть введены в
оператор.
Операнд — число или выражение, на которое действует
оператор.
Например, в выражении 5+3 числа 5 и 3 — операнды
оператора «+» (плюс).
Любой оператор в MathCAD можно ввести двумя способами:
нажав клавишу (сочетание клавиш) на клавиатуре;
используя математическую панель.
18
19.
Для присвоения или вывода содержимого ячейкисвязанной с переменной, используются следующие операторы:
памяти,
знак присвоения — такое присвоение называется
локальным, до этого присваивания переменная не определена
и ее нельзя использовать;
= оператор приближенного равенства (жирное равно) используется при решении уравнений и систем уравнений
блоком Given - Find;
= оператор равенства (простое равно) - отведен для
вывода значения константы или переменной;
глобальный оператор присвоения — это присвоение
может производиться в любом месте документа, к примеру,
если переменной присвоено таким образом значение в самом
конце документа, то она будет иметь это же значение и в начале
документа.
19
20.
Функция – выражение, согласно которому проводятсянекоторые вычисления с его аргументами и определяется его
числовое значение. Функции в пакете MathCAD могут быть
встроенные и определенные пользователем.
Функция пользователя вначале должна быть определена, а
затем к ней может быть произведено обращение. Функция
пользователя определяется следующим образом:
Имя_функции (Переменная) := Выражение
20
21.
Построение двухмерных графиковДля построения двухмерного графика функции
необходимо:
задать диапазон значений аргумента(
);
задать функцию;
установить курсор в то место, где должен быть
построен график, на математической панели выбрать
кнопку двухмерный график;
21
22.
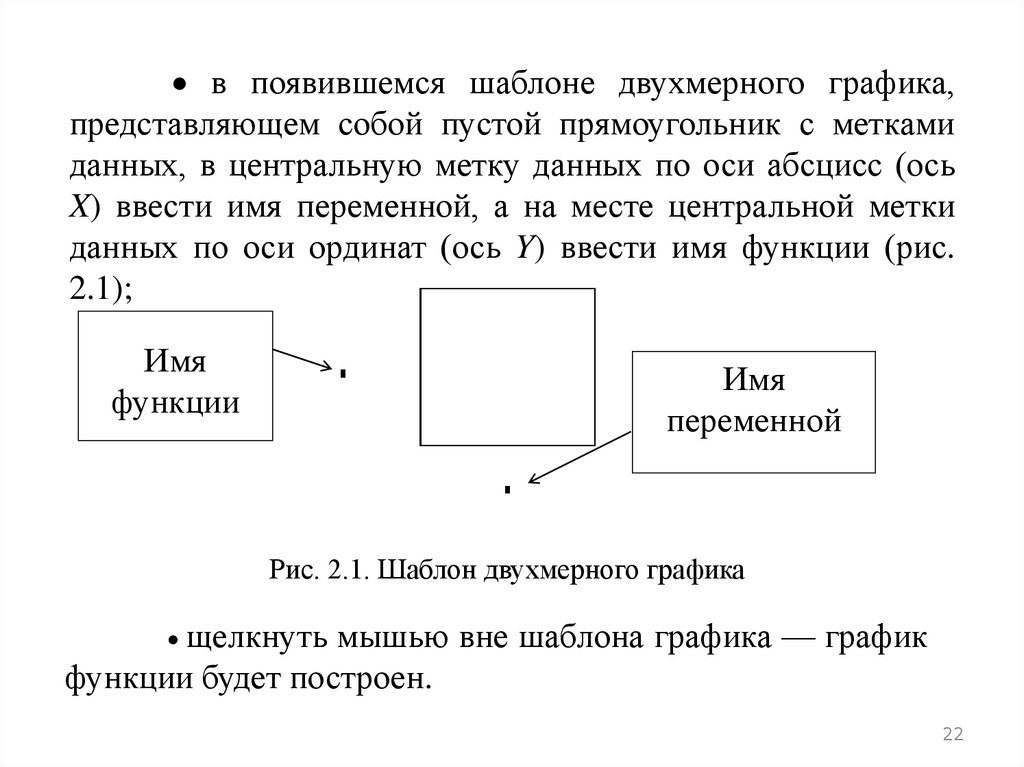
в появившемся шаблоне двухмерного графика,представляющем собой пустой прямоугольник с метками
данных, в центральную метку данных по оси абсцисс (ось
X) ввести имя переменной, а на месте центральной метки
данных по оси ординат (ось Y) ввести имя функции (рис.
2.1);
Имя
функции
Имя
переменной
Рис. 2.1. Шаблон двухмерного графика
щелкнуть мышью вне шаблона графика — график
функции будет построен.
22
23.
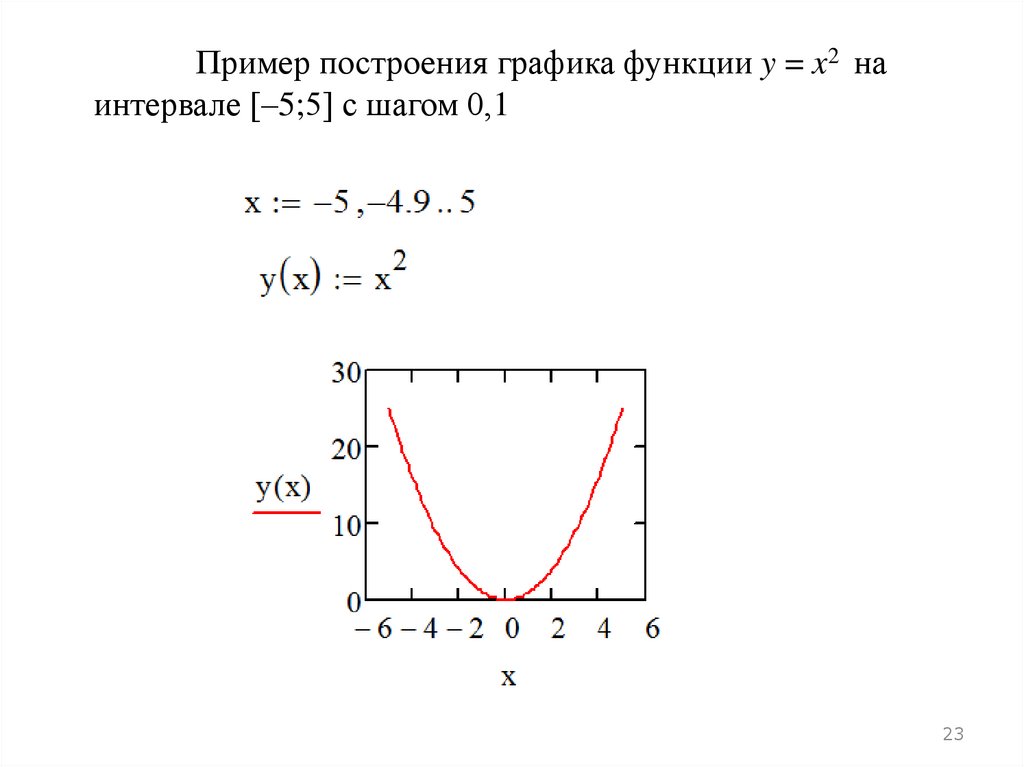
Пример построения графика функции y = x2 наинтервале [–5;5] с шагом 0,1
23
24. Решение уравнений средствами MathCAD
2425.
Решение одного уравнения1-й способ (графический) функция root
Для простейших уравнений вида f(x) = 0 решение в MathCAD находится
с помощью функции root.
root( f(х1, x2, …), х1, a, b )
Возвращает значение х1, принадлежащее отрезку [a, b], при котором
выражение или функция f(х) обращается в 0. Оба аргумента этой функции
должны быть скалярами. Функция возвращает скаляр.
Аргументы:
f(х1, x2, …) - функция, определенная где-либо в рабочем документе, или
выражение. Выражение должно возвращать скалярные значения.
х1 - - имя переменной, которая используется в выражении. Этой переменной
перед использованием функции root необходимо присвоить числовое
значение. Mathcad использует его как начальное приближение при поиске
корня.
a, b - необязательны, если используются, то должны быть вещественными
числами, причем a < b.
25
26.
Внимание. Если правая часть уравнения 0, тонеобходимо привести его к нормальному виду
(перенести все в левую часть).
Перед использованием функции root необходимо
задать аргументу х начальное приближение. Если
корней несколько, то для отыскания каждого корня
необходимо задавать свое начальное приближение.
Внимание. Перед решением желательно построить
график функции, чтобы проверить, есть ли корни
(пересекает ли график ось абсцисс ОХ), и если есть, то
сколько. Начальное приближение можно выбрать по
графику поближе к точке пересечения
!
26
27.
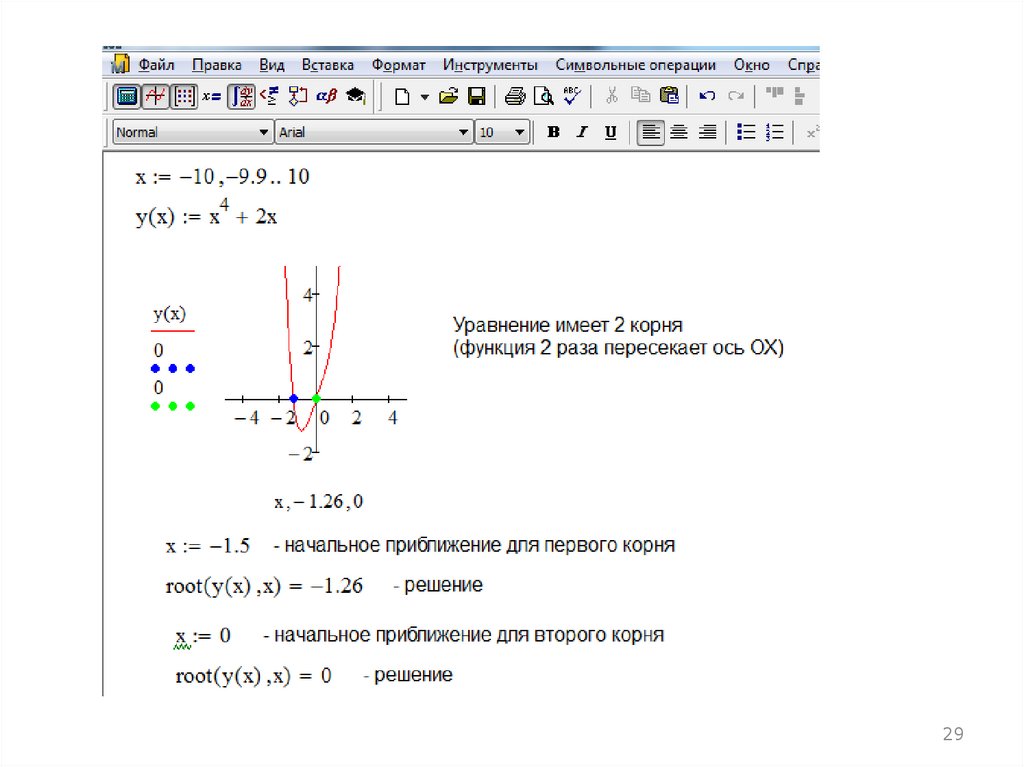
Пример. Решение уравнения x4 = -2x с помощью функции root. Перед тем какприступить к решению в системе MathCAD, в уравнении все перенесем в левую
часть. Уравнение примет вид: x4 +2x = 0
27
28.
2829.
2930.
)30
31.
2-й способ функция polyrootsДля нахождения корней выражения, имеющего вид
vnxn + ... + v2x2 + v1x + v0,
лучше использовать функцию polyroots, нежели root. В отличие от
функции root, функция polyroots не требует начального приближения
и возвращает сразу все корни, как вещественные, так и комплексные.
Polyroots(v)
Возвращает корни полинома степени n. Коэффициенты полинома
находятся в векторе v длины n + 1. Возвращает вектор длины n,
состоящий из корней полинома.
Аргументы:
v - вектор, содержащий коэффициенты полинома.
31
32.
Пример. Решение уравненияс помощью функции polyroots.
32
33.
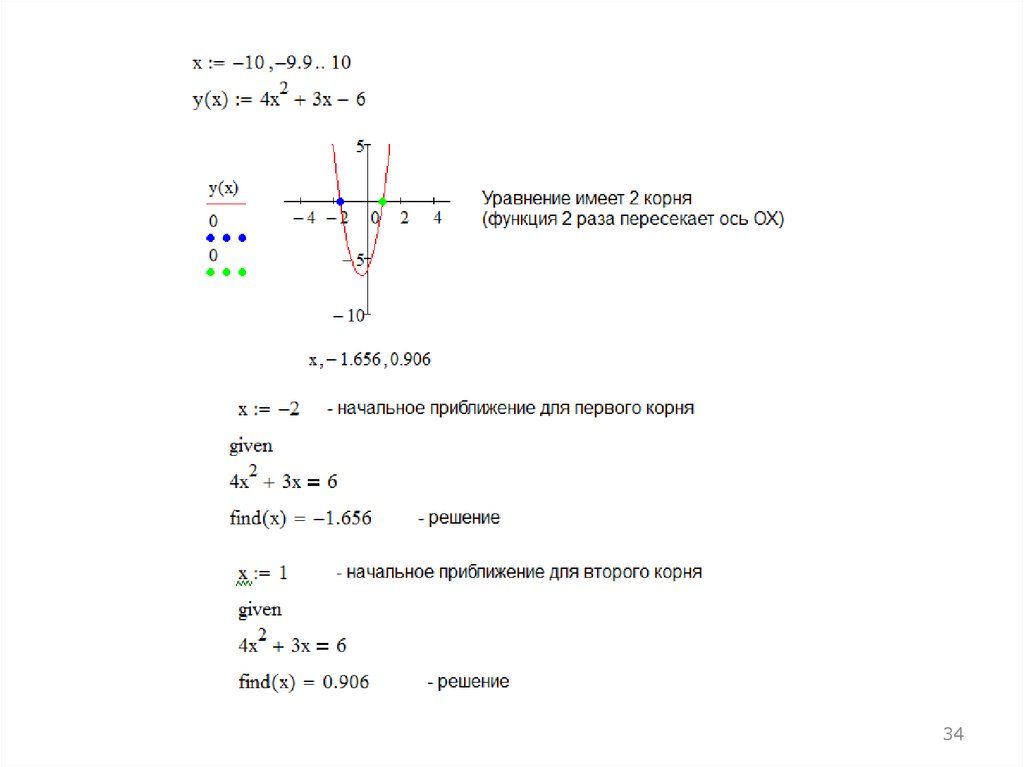
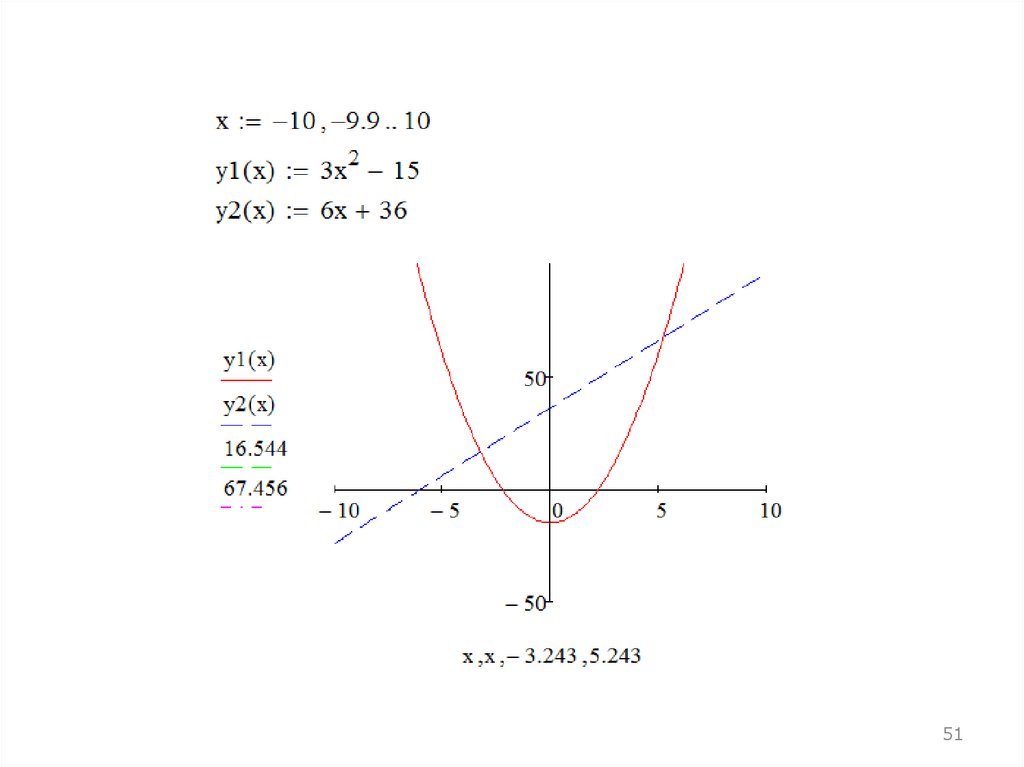
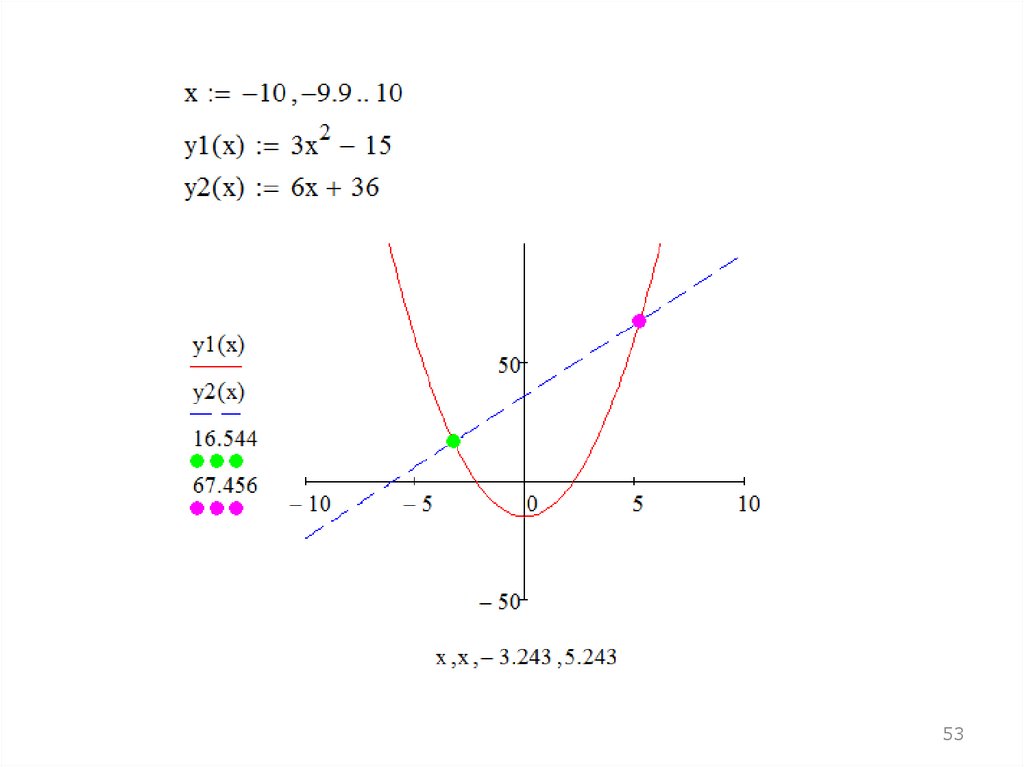
3-й способ (графический) блок given - findПример. Решение уравнения y = 4x2 +3x – 6
33
34.
3435.
Решение систем уравненийMathCAD дает возможность решать также и системы уравнений.
Максимальное число уравнений и переменных равно 50. Результатом решения
системы будет численное значение искомого корня.
Для решения системы уравнений необходимо выполнить следующее:
•Задать начальное приближение для всех неизвестных, входящих в систему
уравнений. Mathcad решает систему с помощью итерационных методов.
•Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует
система уравнений.
•Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для
печати символа =. Между левыми и правыми частями неравенств может
стоять любой из символов <, >,
и
.
•Введите любое выражение, которое включает функцию Find,
например: а:= Find(х, у).
Find(z1, z2, . . .)
35
36.
Возвращает точное решение системы уравнений. Числоаргументов должно быть равно числу неизвестных.
Ключевое слово Given, уравнения и неравенства, которые
следуют за ним, и какое-либо выражение, содержащее функцию Find,
называют блоком решения уравнений.
Следующие выражения недопустимы внутри блока решения:
•Ограничения со знаком
.
•Дискретный аргумент или выражения, содержащие дискретный
аргумент в любой форме.
•Неравенства вида a < b < c.
Блоки решения уравнений не могут быть вложены друг в друга,
каждый блок может иметь только одно ключевое слово Given и имя
функции Find.
Функция, которая завершает блок решения уравнений, может
быть использована аналогично любой другой функции. Можно
произвести с ней следующие три действия:
36
37.
•Можно вывести найденное решение, напечатав выражение вида:Find(var1, var2,…) =.
•Определить переменную с помощью функции Find:
a := Find(x) - скаляр,
var := Find(var1, var2,…) - вектор.
Это удобно сделать, если требуется использовать решение
системы уравнений в другом месте рабочего документа.
•Определить другую функцию с помощью Find
f(a, b, c, …) := Find(x, y, z, …).
Эта конструкция удобна для многократного решения
системы уравнений для различных значений некоторых
параметров a, b, c, …, непосредственно входящих в систему
уравнений.
37
38.
.Решение систем уравнений
1. Решение систем линейных уравнений
Систему
линейных
уравнений
можно
решить матричным методом (или через обратную
матрицу или используя функцию lsolve(A,B)) и с
использованием
двух
функций
Find
и
функции Minerr.
38
39.
1-й способ Матричный методПример. Дана система уравнений:
39
40.
2-й способ функция lsolve(A,B)Lsolve(A,B) — это встроенная функция, которая
возвращает вектор Х для системы линейных уравнений
А*Х=В при заданной матрице коэффициентов А и
векторе свободных членов В.
40
41.
Пример. Дана система уравнений:41
42.
3-й способ с помощью блока Given – FindПри данном методе уравнения вводятся без использования
матриц, т.е. в «натуральном виде». Предварительно необходимо
указать начальные приближения неизвестных переменных. Это
могут быть любые числа, входящие в область определения. Часто
за них принимают столбец свободных членов.
Для того чтобы решить систему линейных уравнений с
помощью вычислительного блока Given – Find, необходимо:
1) задать начальные приближения для всех переменных;
2) ввести служебное слово Given;
3) записать систему уравнений, используя знак жирное
равно(=);
4) написать функцию Find, перечислив неизвестные переменные
в качестве параметров функции.
В результате расчетов выведется вектор решения системы.
42
43.
Пример. Дана система уравнений:43
44.
Приближенное решение системы линейныхуравнений
Решение системы линейных уравнений с помощью
функцию Minerr аналогично решению с помощью
функции Find (используется тот же алгоритм), только
функция Find дает точное решение, а Minerr —
приближенное. Если в результате поиска не может
быть получено дальнейшее уточнение текущего
приближения к решению, Minerr возвращает это
приближение. Функция Find в этом случае
возвращает сообщение об ошибке.
44
45.
Общие рекомендации по решению уравнений и системуравнений
Ниже перечислены некоторые рекомендации, которые
следует
выполнять,
если
MathCAD
не
может
самостоятельно найти решение.
· Можно подобрать другое начальное приближение.
· Можно увеличить или уменьшить точность расчетов.
Для этого в меню выбрать Math ► Options (Математика –
Опции), вкладка Built-In Variables (Встроенные
переменные). В открывшейся вкладке необходимо
уменьшить
допустимую
погрешность
вычислений
(Convergence Tolerance (TOL)). По умолчанию TOL = 0.001.
Внимание. При матричном методе решения необходимо
переставить
коэффициенты
согласно
возрастанию
неизвестных х1, х2, х3, х4.
45
46.
2. Решение систем нелинейных уравненийСистемы нелинейных уравнений в MathCAD решаются
с
помощью вычислительного блока Given –Find.
Конструкция Given – Find использует расчетную методику,
основанную на поиске корня вблизи точки начального
приближения, заданной пользователем.
Для решения системы уравнений с помощью блока Given –
Find необходимо:
1) задать начальные приближения для всех переменных;
2)
ввести служебное слово Given;
3) записать систему уравнений, используя знак жирное
равно(=);
4) написать функцию Find, перечислив неизвестные переменные
в качестве параметров функции.
46
47.
В результате расчетов выведется вектор решениясистемы.
Если система имеет несколько решений, алгоритм
следует
повторить
с
другими
начальными
приближениями.
Примечание. Если решается система из двух
уравнений с двумя неизвестными, перед решением
желательно построить графики функций, чтобы
проверить, есть ли корни у системы (пересекаются ли
графики заданных функций), и если есть, то сколько.
Начальное приближение можно выбрать по графику
поближе к точке пересечения.
47
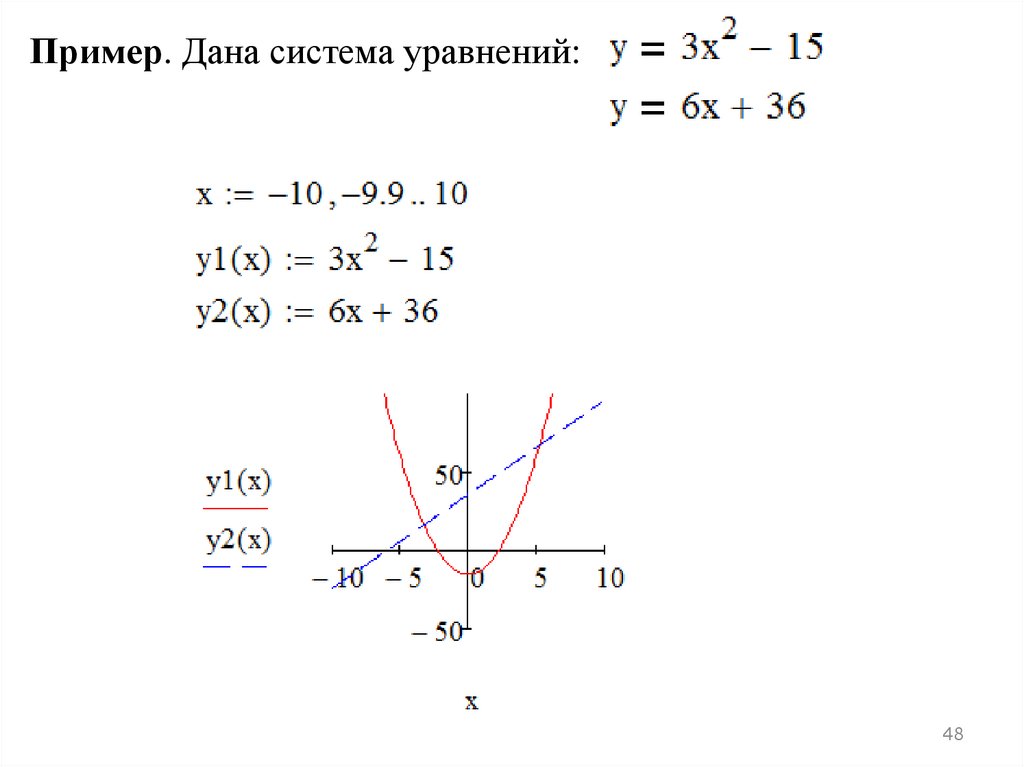
48.
Пример. Дана система уравнений:48
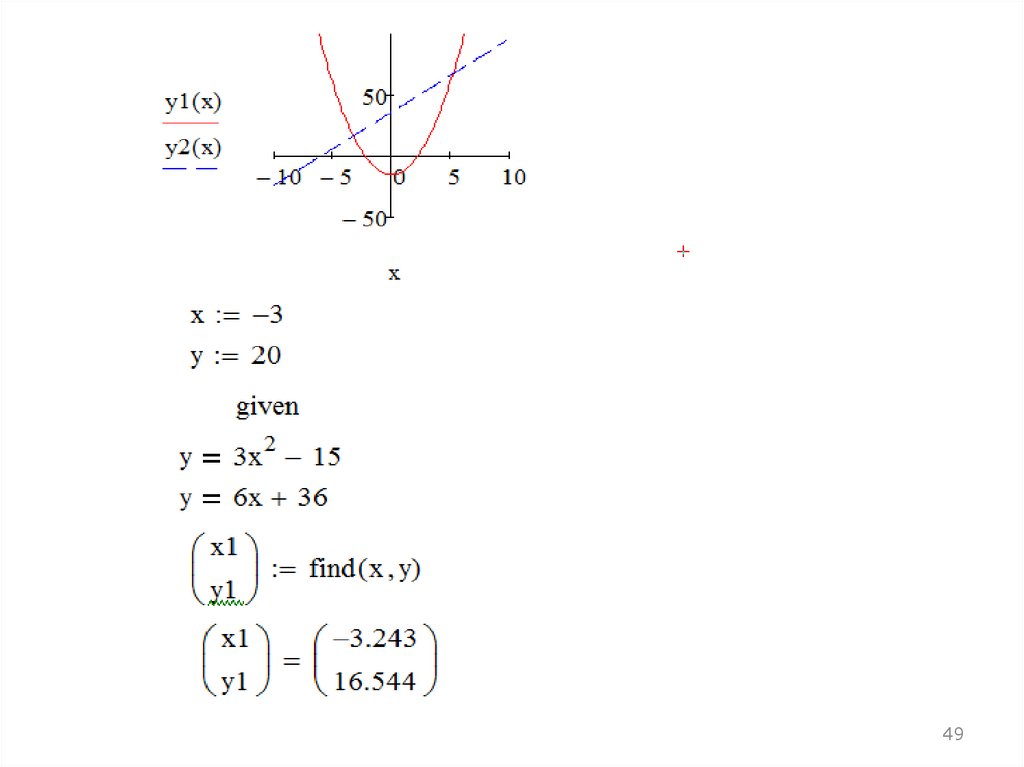
49.
4950.
5051.
5152.
5253.
5354.
5455.
Нахождение локальных экстремумовфункций
Необходимое условие экстремума (максимума и/или
минимума) непрерывной функции формулируется так:
экстремумы могут иметь место только в тех точках, где
производная или равна нулю, или не существует (в
частности, обращается в бесконечность). Для нахождения
экстремумов непрерывной функции сначала находят точки,
удовлетворяющие необходимому условию, то есть находят
все действительные корни уравнения
Если построен график функции, то можно сразу увидеть
— максимум или минимум достигается в данной точке х.
Если графика нет, то каждый из найденных корней
исследуют одним из способов.
55
56.
1-й способ. Сравнение знаков производной.Определяют знак производной в окрестности точки (в
точках, отстоящих от экстремума функции по разные
стороны на небольших расстояниях). Если знак
производной при этом меняется от «+» к «–»,
то в данной точке функция имеет максимум.
Если знак меняется от «–» к «+» , то в
данной точке функция имеет минимум. Если
знак
производной
не
меняется,
то
экстремумов не существует.
56
57.
2-й способ. Вычисление второй производной.В этом случае вычисляется вторая производная в точке
экстремума. Если вторая производная меньше
нуля, то в данной точке функция имеет
максимум, если вторая производная больше
нуля, то минимум.
57
58.
Сначала построим график функцииОпределим по графику начальные приближения значений х,
соответствующих локальным экстремумам функции f(x). Найдем эти
экстремумы, решив уравнение
58
59.
Для решения используем блок Given – Find59
60.
Определим вид экстремумов первым способом, исследуя изменение знакапроизводной в окрестности найденных значений
60
61.
Из таблицы значений производной и из графикавидно, что знак производной в окрестности точки x1
меняется с плюса на минус, поэтому в этой точке
функция достигает максимума. А в окрестности
точки x2 знак производной поменялся с минуса на
плюс, поэтому в этой точке функция достигает
минимума.
61
62.
Определим вид экстремумов вторым способом, вычисляя знаквторой производной
Видно, что в точке x1 вторая производная меньше нуля, значит,
точка х1 соответствует максимуму функции. А в точке x2 вторая
производная больше нуля, значит, точка х2 соответствует минимуму
функции.
62
63.
.Определение площадей фигур,
ограниченных непрерывными линиями
Площадь криволинейной трапеции, ограниченной
графиком функции f(x), отрезком [a,b] на оси OХ и
двумя вертикалями х = а и х = b, a < b, определяется по
формуле:
63
64.
Пример. Нахождение площадилиниями f(x) = 1 – x2 и y = 0.
фигуры,
ограниченной
64
65.
Площадь фигуры, заключенной между графикамифункций f1(x) и f2(x) и прямыми х = а и х = b,
вычисляется по формуле:
b
S f 1( x) f 2( x) dx
a
Внимание. Чтобы избежать ошибок при вычислении
площади, разность функций надо брать по модулю. Таким
образом, площадь будет всегда положительной величиной.
65
66.
Пример. Нахождение площади фигуры, ограниченнойфункциями
f 1( x) 1 x2
и
f 2( x) x2 2
1. Строим график функций.
2. Находим точки пересечения функций с помощью
функции root. Начальные приближения определим по
графику
.
3. Найденные значения x подставляем в формулу
b
S f 1( x) f 2( x) dx
a
как пределы интегрирования.
66
67.
6768.
Построение кривых по заданным точкамПостроение прямой, проходящей через две
заданные точки
Для составления уравнения прямой, проходящей через
две точки А(x0, y0) и B(x1, y1), предлагается
следующий алгоритм:
1. Прямая задается уравнением y = ax + b,
где a и b — коэффициенты прямой, которые нам
требуется найти.
Подставляем в это уравнение заданные
координаты точек и получаем систему:
y0 a x0 b
y1 a x1 b
68
69.
2. Данная система является линейной. В ней двенеизвестные переменные: a и b. Систему можно
решить матричным способом.
Пример. Построение прямой, проходящей через
точки А(–2, –4) и В(5, 7).
Подставим в уравнение прямой координаты
данных точек и получим систему:
4 2 a b
7 5 a b
69
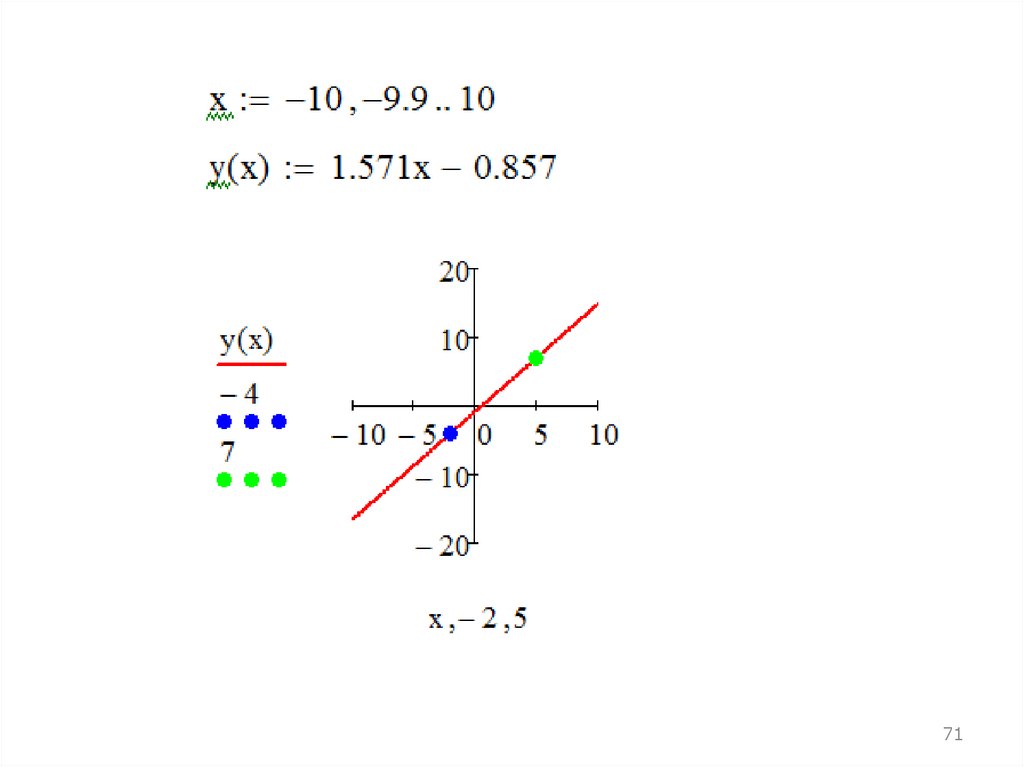
70.
Решение этой системы в MathCADВ результате решения системы получаем:
а = 1.571, b = –0.857. Значит, уравнение прямой будет
иметь вид: y = 1.571x – 0.857. Построим эту прямую
70
71.
7172.
Построение параболы, проходящей черезтри заданные точки
Для построения параболы, проходящей через три
точки А(x0, y0), B(x1, y1) и C(x2, y2), алгоритм
следующий:
1. Парабола задается уравнением
2
y = ax + bх + с
где а, b и с — коэффициенты параболы, которые нам
требуется найти.
72
73.
Подставляем в это уравнение заданные координатыточек и получаем систему:
y0 a x0 b x0 c
y1 a x1 b x1 c
y2 a x2 b x2 c
2. Данная система является линейной. В ней три
неизвестные переменные: a, b и с. Систему можно
решить матричным способом.
3. Полученные коэффициенты подставляем в
уравнение и строим параболу.
73
74.
Пример. Построение параболы, проходящей черезточки А(–1, –4), B(1, –2) и C(3, 16).
Подставляем
в
уравнение
параболы
заданные
координаты точек и получаем систему:
4 a ( 1) 2 b ( 1) c
2
2
a
1
b 1 c
2
16
a
3
b 3 c
74
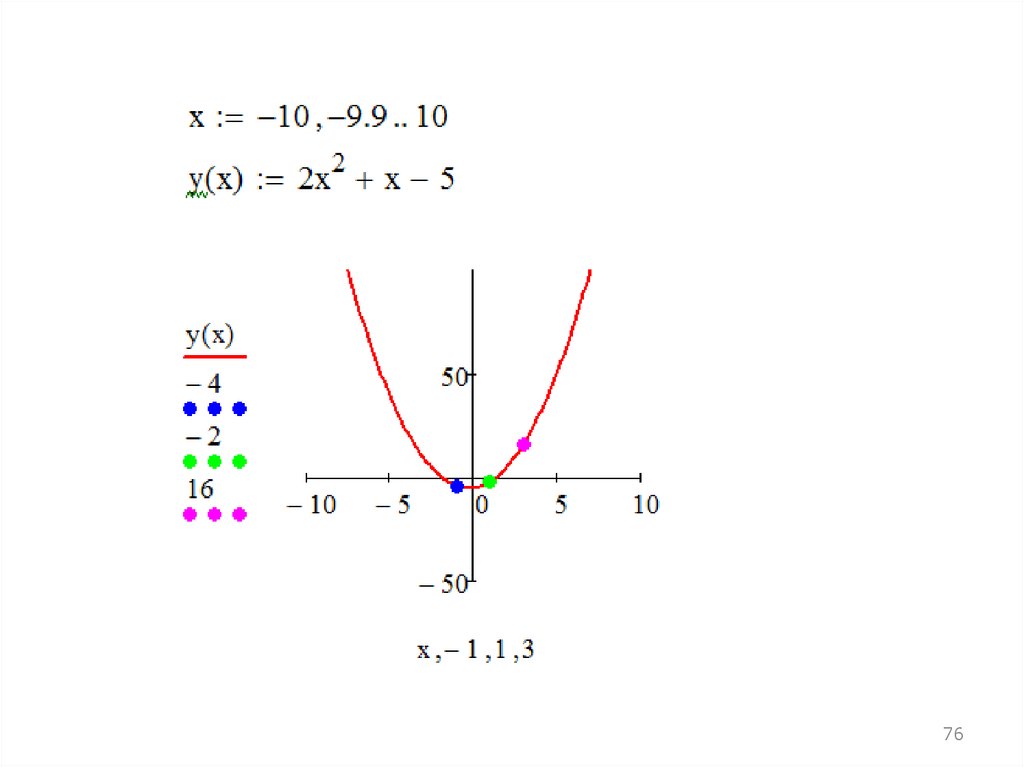
75.
Решение этой системы уравнений в MathCADВ результате получены коэффициенты: a=2, b=1, c= –5.
Получаем
уравнение
параболы:
y=2x2+x–5.
Построим эту параболу
75
76.
7677.
Построение окружностиПостроение окружности с центром в точке O(2;3) и радиусом
R=6.
Уравнение окружности с центром в точке с координатами
(x0, y0) и радиусом R записывается в виде:
x x0 y y0 R
2
2
2
.
Выразим из этого уравнения y:
y y0 R x x0 ;
2
2
2
y y0 R x x0 ;
2
2
y R x x0 y0 .
2
2
77
78.
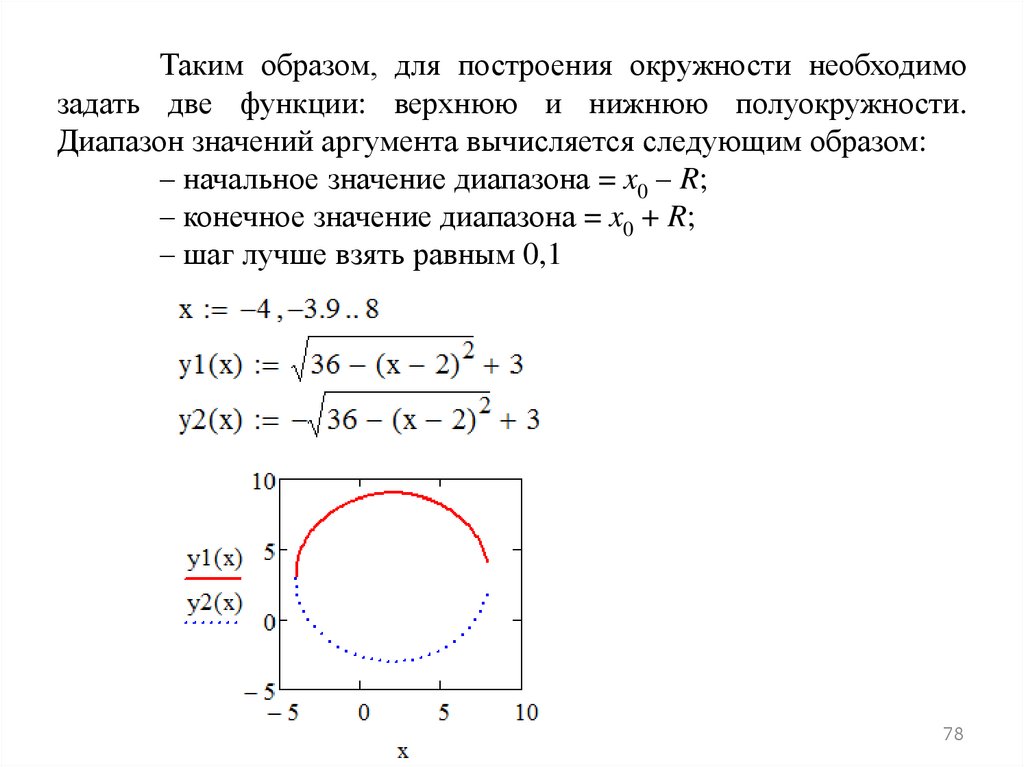
Таким образом, для построения окружности необходимозадать две функции: верхнюю и нижнюю полуокружности.
Диапазон значений аргумента вычисляется следующим образом:
– начальное значение диапазона = x0 – R;
– конечное значение диапазона = x0 + R;
– шаг лучше взять равным 0,1
78
79.
Построение окружности, проходящей черезтри заданные точки
Для построения окружности, проходящей через три
точки А(x1,y1), B(x2,y2) и C(x3,y3), можно
воспользоваться следующим алгоритмом:
1.
Окружность задается уравнением
x x0 y y0 R
2
2
2
где x0,y0 — координаты центра окружности;
R — радиус окружности.
79
80.
2. Подставим в уравнение окружности заданныекоординаты точек и получим систему:
( x1 x0) 2 ( y1 y 0) 2 R 2
2
2
2
( x 2 x0) ( y 2 y 0) R
2
2
2
( x3 x0) ( y3 y 0) R
Данная система является нелинейной. В ней три
неизвестные переменные: x0, y0 и R. Система решается
с применением вычислительного блока Given – Find.
80
81.
Пример. Построение окружности, проходящей черезтри точки А(–2; 1), B(6; 0) и C(2; 4).
Подставим
в
уравнение
окружности
заданные
координаты точек и получим систему:
( 2 x0) 2 (1 y 0) 2 R 2
2
2
2
(6 x0) (0 y 0) R
2
2
2
(2 x0) (4 y 0) R
81
82.
Решение системы в MathCAD82
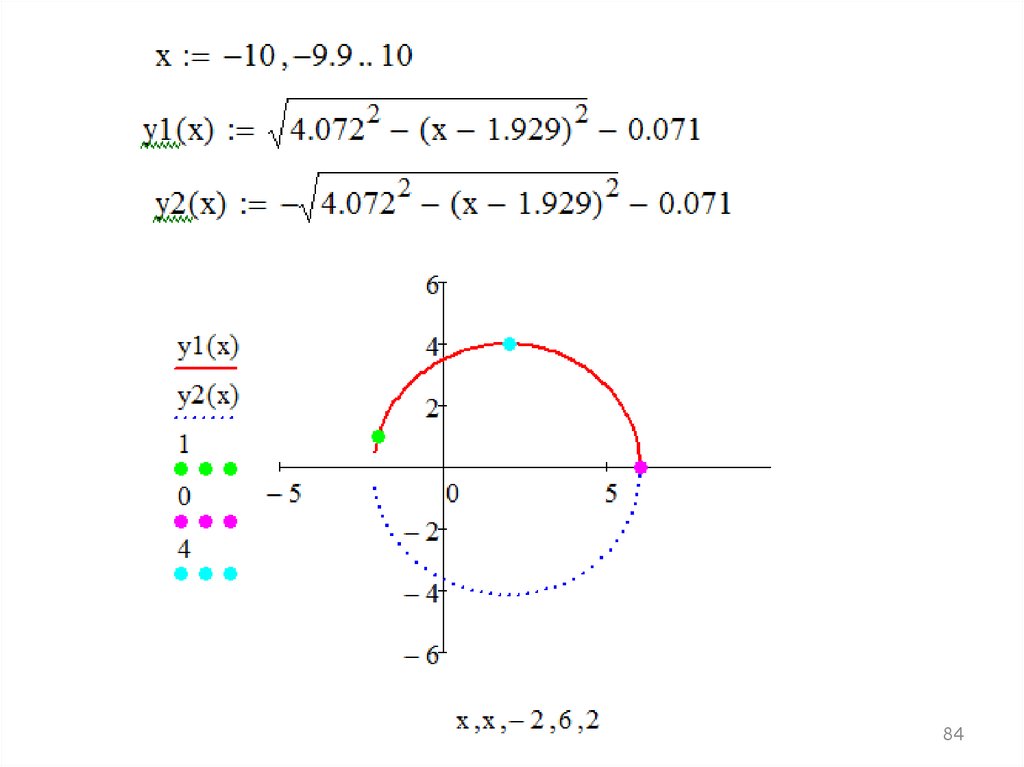
83.
В результате решения системы получено:x0 = 1.929, y0 = -0.071, R = 4.072.
Подставим
полученные
координаты
центра
окружности и радиус в уравнение окружности.
Получим: ( x 1.929 ) 2 ( y 0.071) 2 4.072 2
Выразим отсюда y и построим окружность
83
84.
8485.
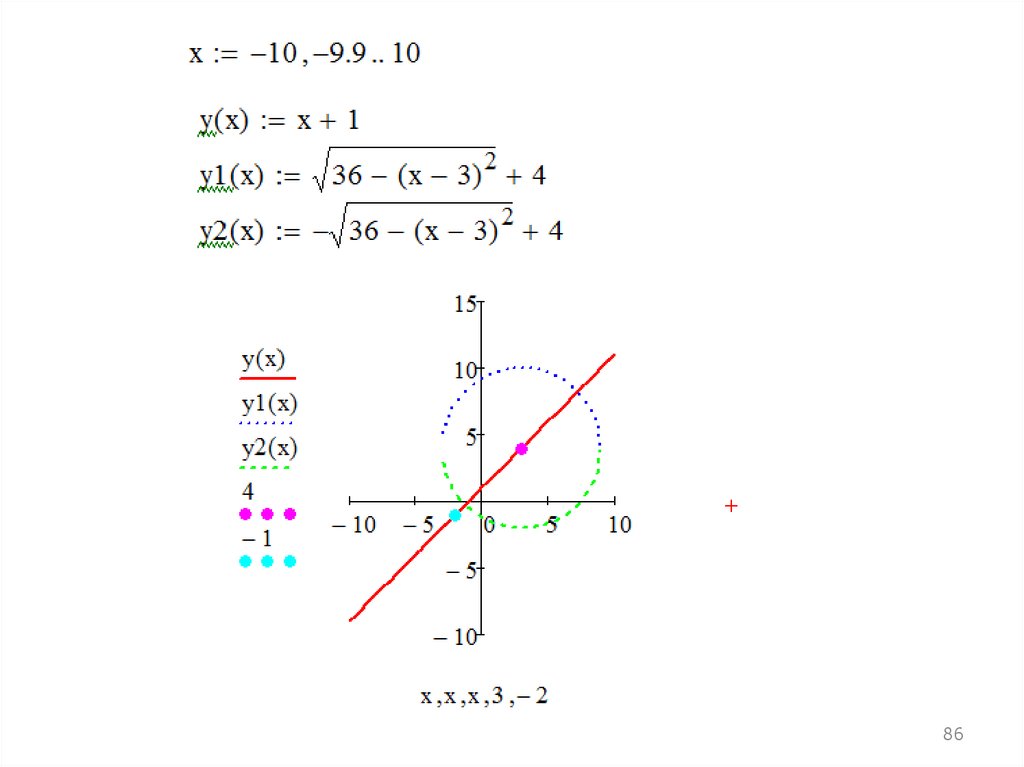
Решение инженерных задач1) Дана окружность с центром в точке О(3; 4) и радиусом
R = 6. Прямая проходит через центр окружности и точку
А (–2, –1). Построить окружность и прямую и найти их
точки пересечения.
85
86.
8687.
8788.
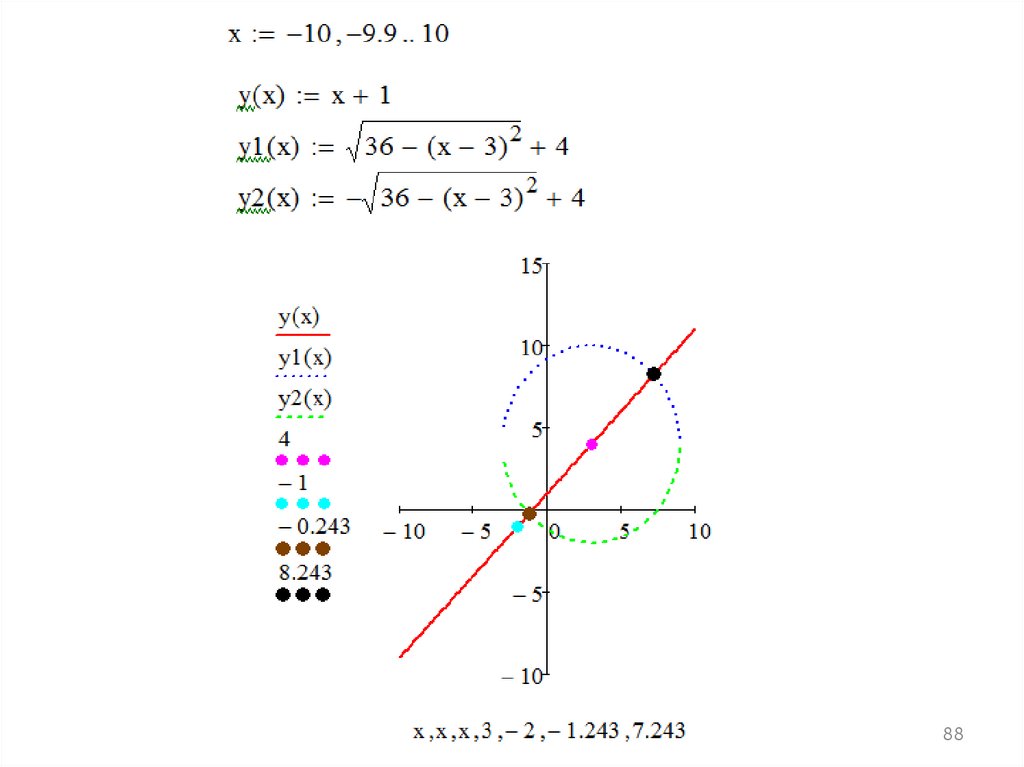
8889.
8990.
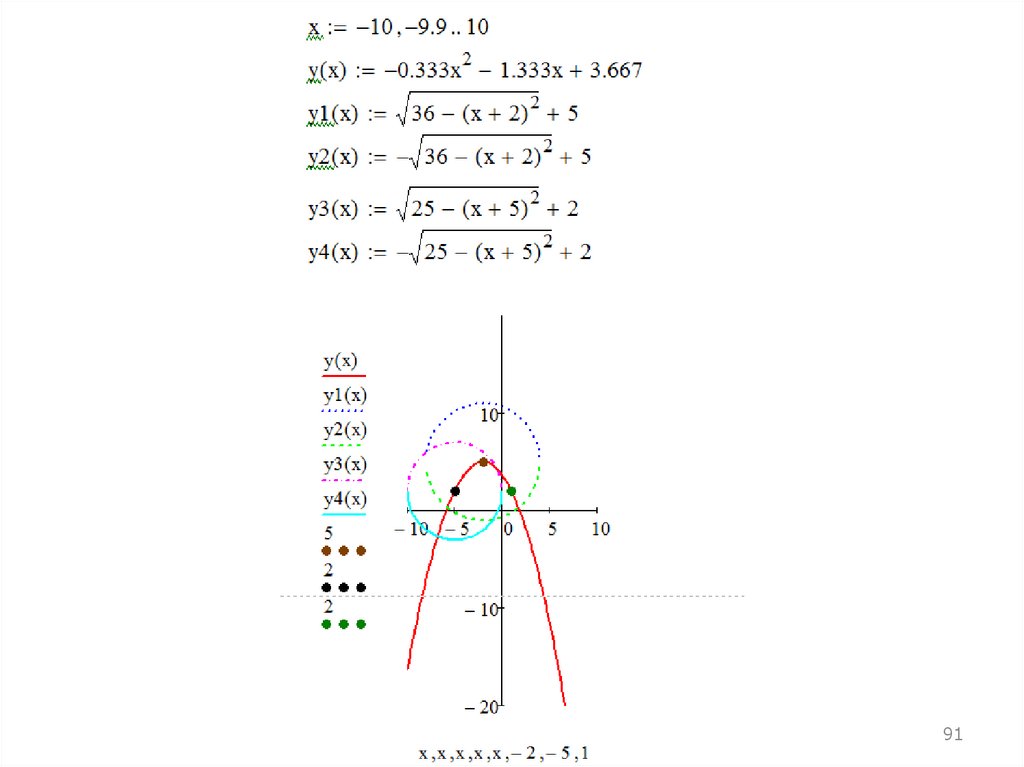
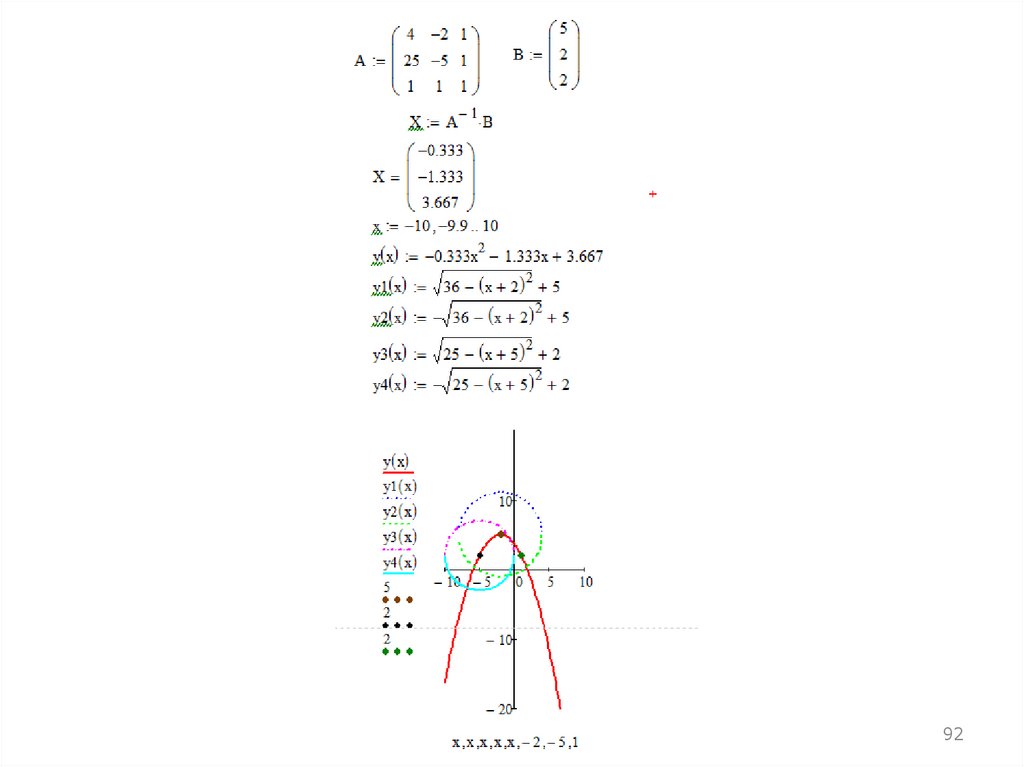
2) Дано: А(–2, 5) и В(–5, 2) — координаты центров двухокружностей.
R1 = 6; R2 = 5 — их радиусы.
Построить эти окружности и параболу, проходящую через
центры окружностей и точку С(1, 2).
90






































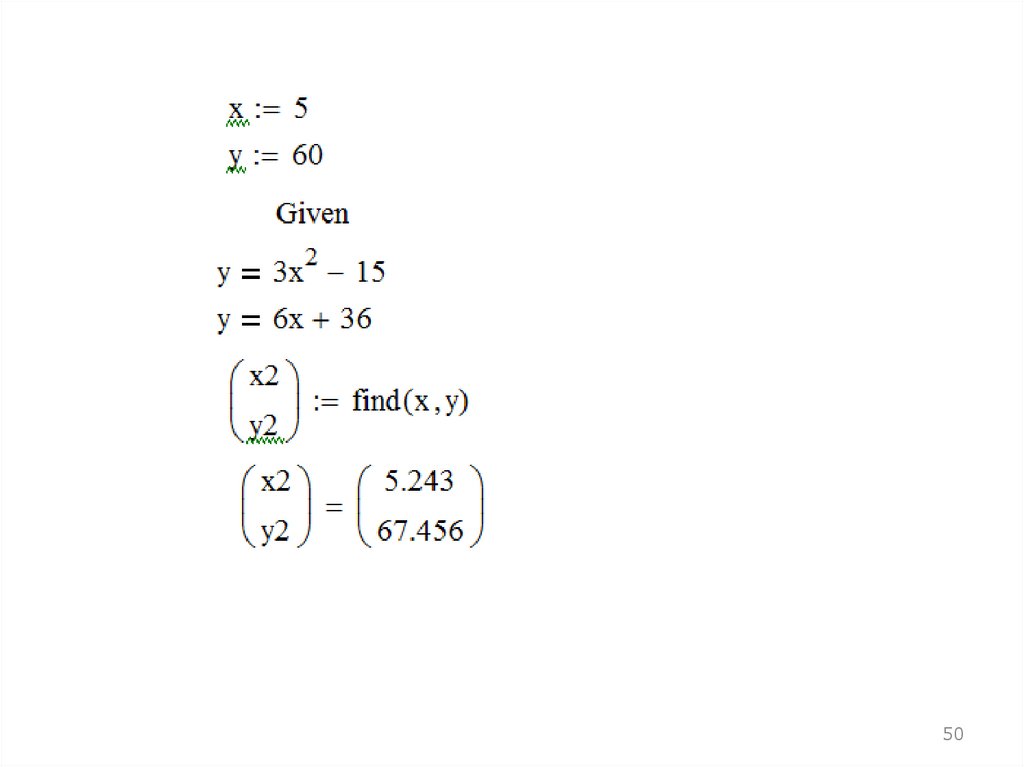































 mathematics
mathematics








