Электромагнитные колебания

1.

Подготовлено:
Учителем физики
Агеевой Л.А.
МБОУСОШ №49
Для учащихся 11 класса

2.

точное или приближенное повторение какого-либо
процесса с течением времени
Механические колебания
Электромагнитные колебания
Другие колебания

3.

физические величины, описывающие колебательный
процесс и сами испытывающие повторяющиеся
изменения.
Механические колебания
координата, скорость,
ускорение, энергия и т.д.
Электромагнитные колебания
сила тока, напряжение, заряд
конденсатора, энергия и т.д.

4.

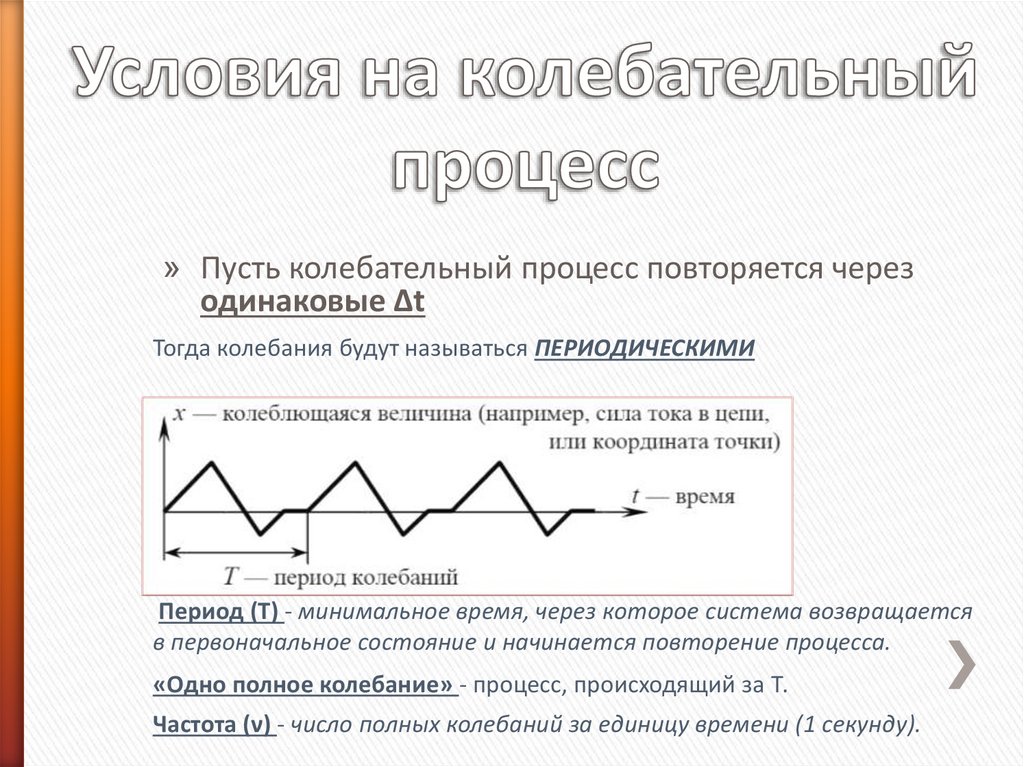
» Пусть колебательный процесс повторяется через
одинаковые ∆t
Тогда колебания будут называться ПЕРИОДИЧЕСКИМИ
Период (T) - минимальное время, через которое система возвращается
в первоначальное состояние и начинается повторение процесса.
«Одно полное колебание» - процесс, происходящий за Т.
Частота (ν) - число полных колебаний за единицу времени (1 секунду).

5.

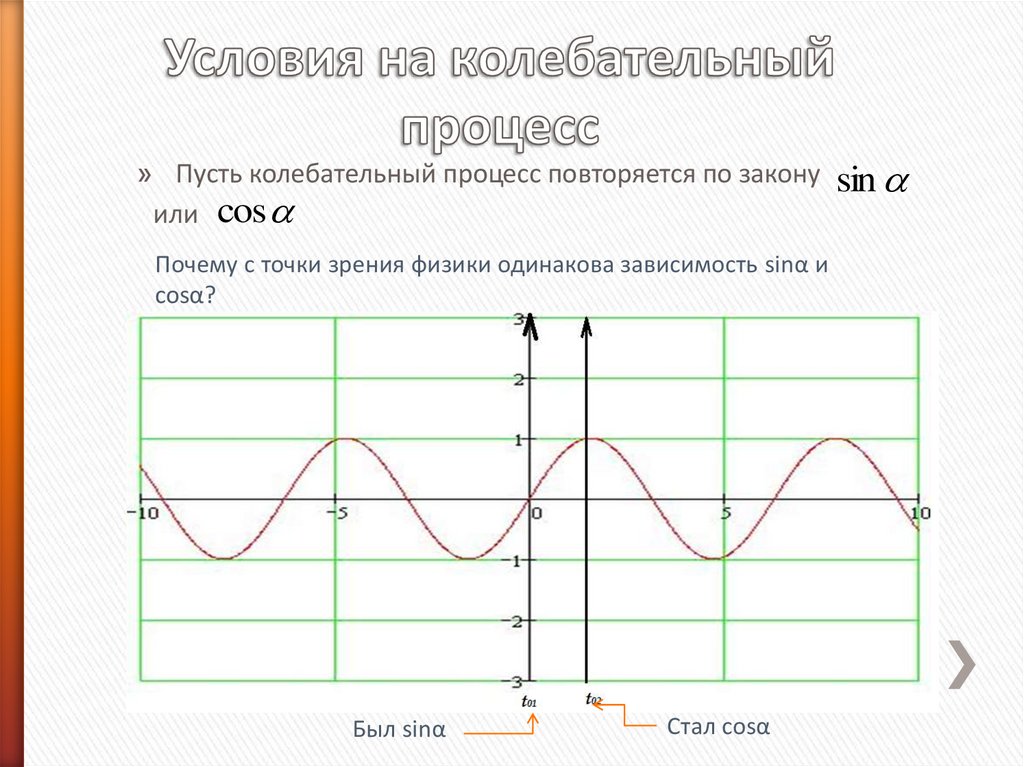
» Пусть колебательный процесс повторяется по закону
или cos
Почему с точки зрения физики одинакова зависимость sinα и
cosα?
Был sinα
Стал cosα
sin

6.

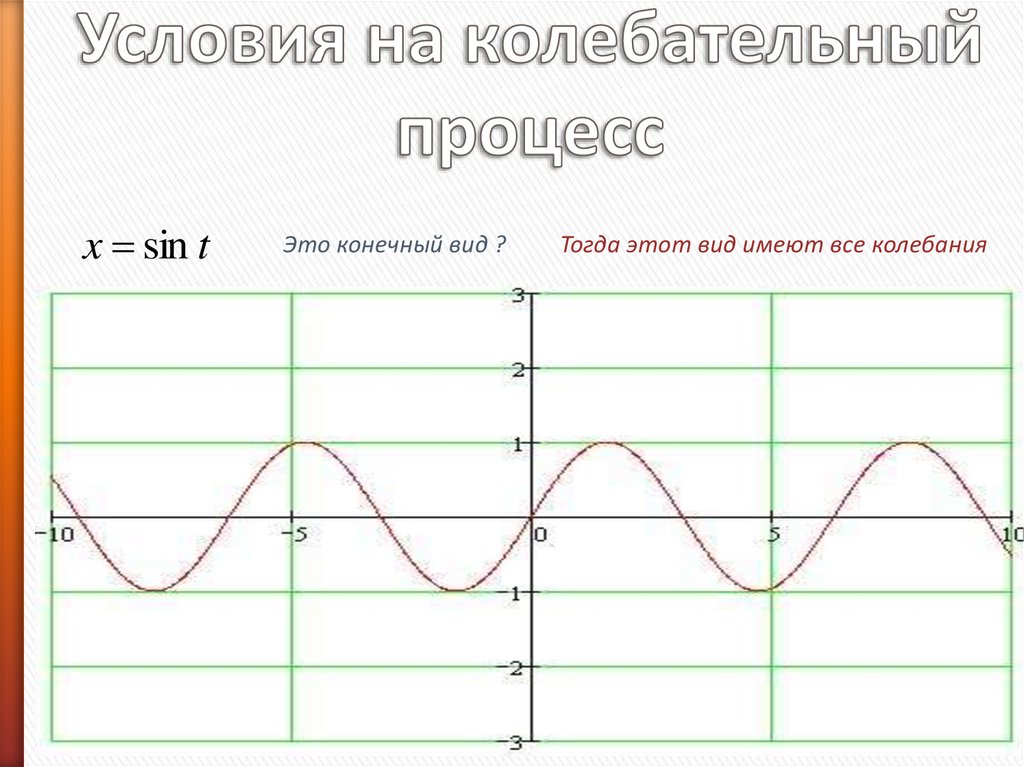
x sin t
Это конечный вид ?
Тогда этот вид имеют все колебания

7.

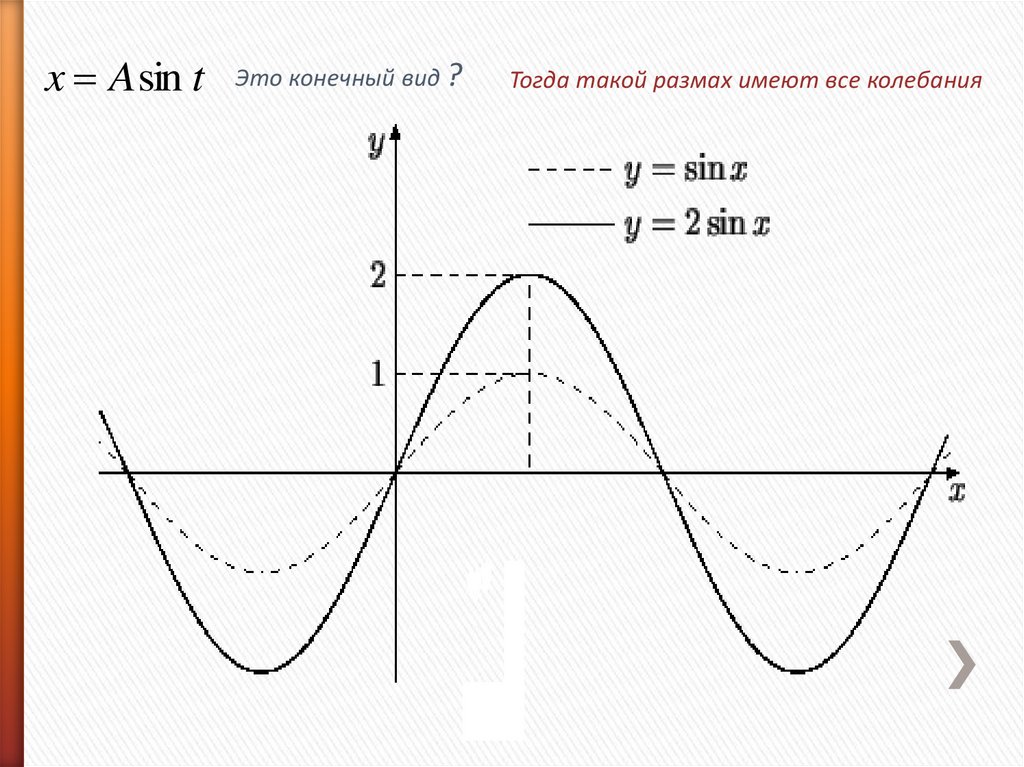
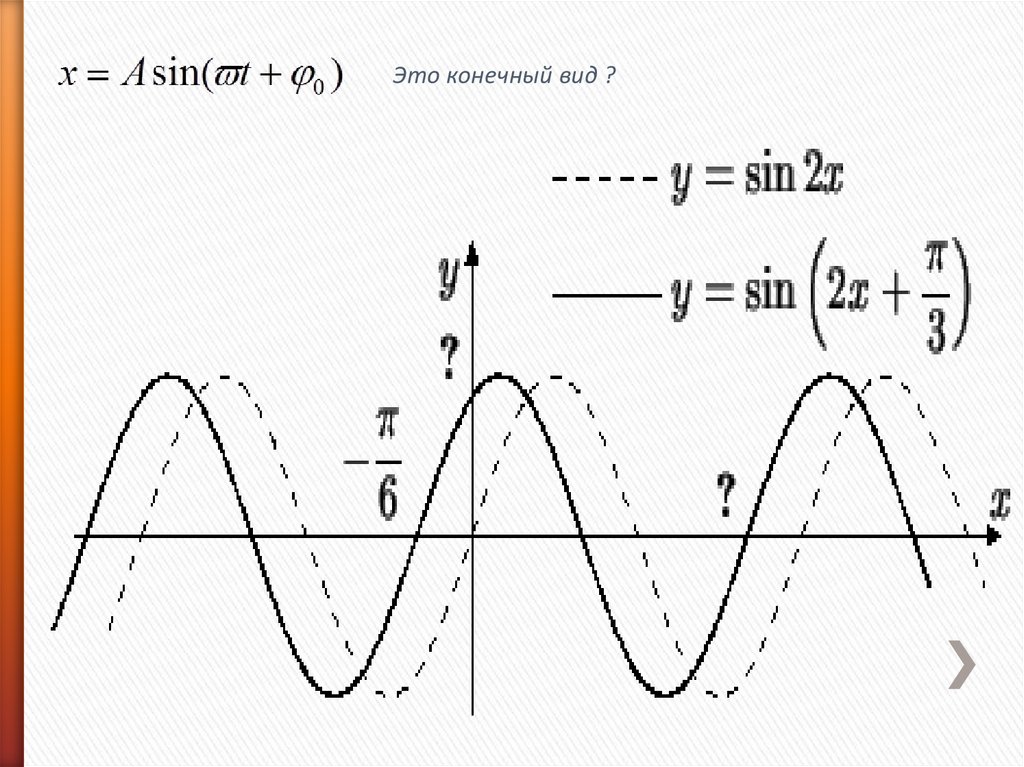
x Asin t
Это конечный вид ?
Тогда такой размах имеют все колебания

8.

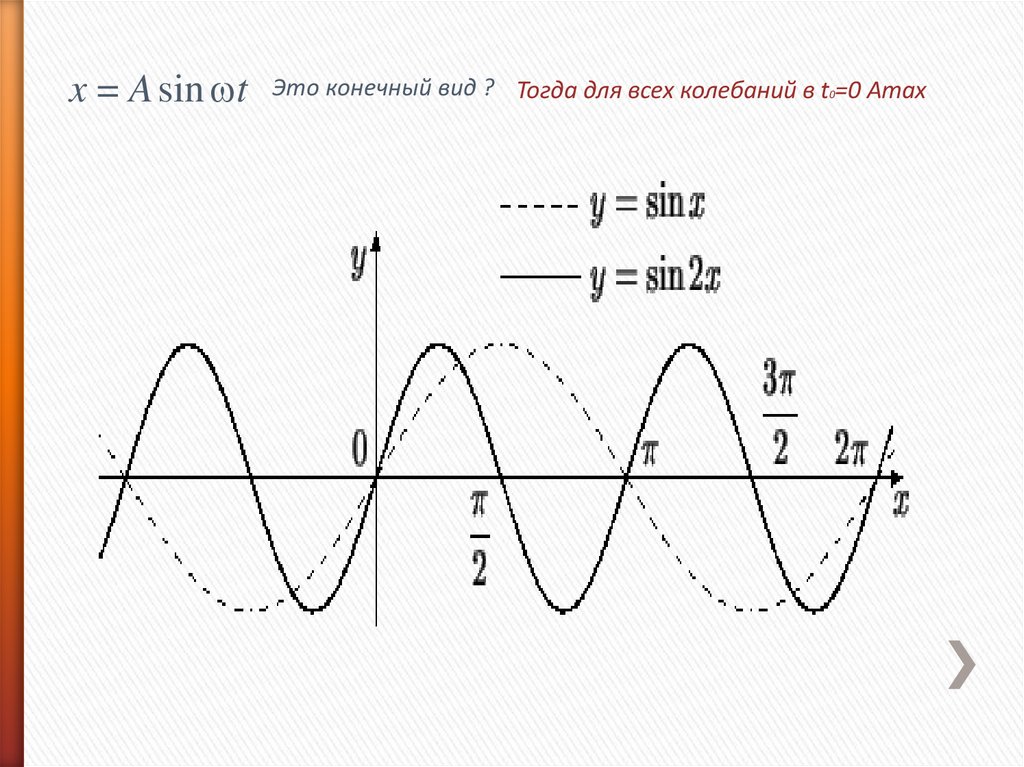
x = A sin wt
Это конечный вид ? Тогда для всех колебаний в t0=0 Amax

9.

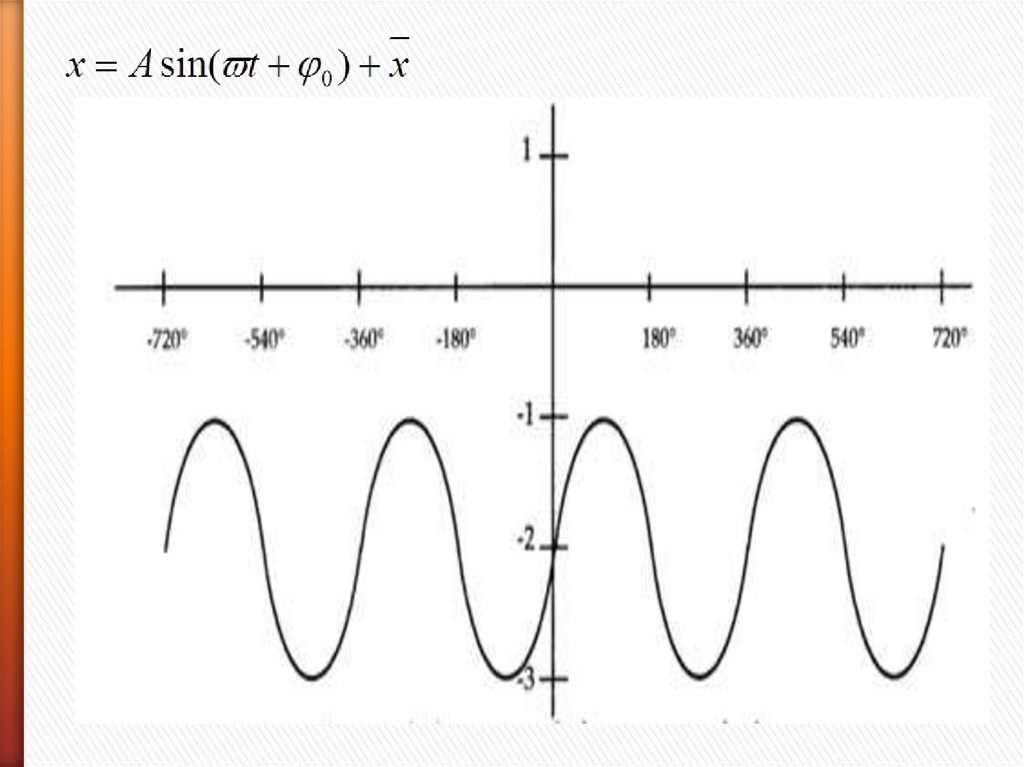
Это конечный вид ?

10.

11.

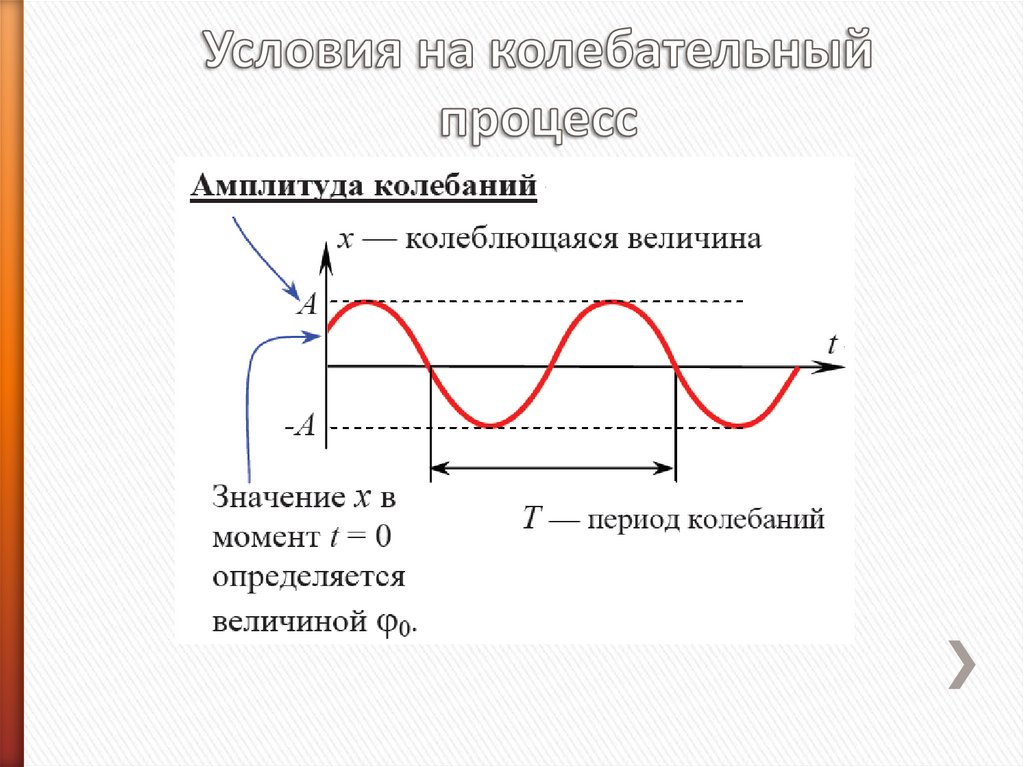
Где:
x – колеблющаяся величина (координата точки, сила тока, напряжённость поля, или
иная величина)
A – амплитуда колебаний – максимальное отклонение колеблющейся величины от
среднего за период значения.
Если среднее за период значение колеблющейся величины=0, то амплитуда равна
максимальному значению колеблющейся величины: А=
-начальная фаза- значение фазы
в момент t=0.
Изменяя значение
, можно получать различные значения x в момент t=0.
- Фаза колебаний – аргумент функции синус или косинус в уравнении
зависимости колеблющейся величины от времени.
- циклическая частота колебаний - скорость изменения фазы с течением времени.
Изменение фазы, произошедшее за время
Т. к. функции sin и cos повторяют свои значения
при изменении аргумента на 2π

12.

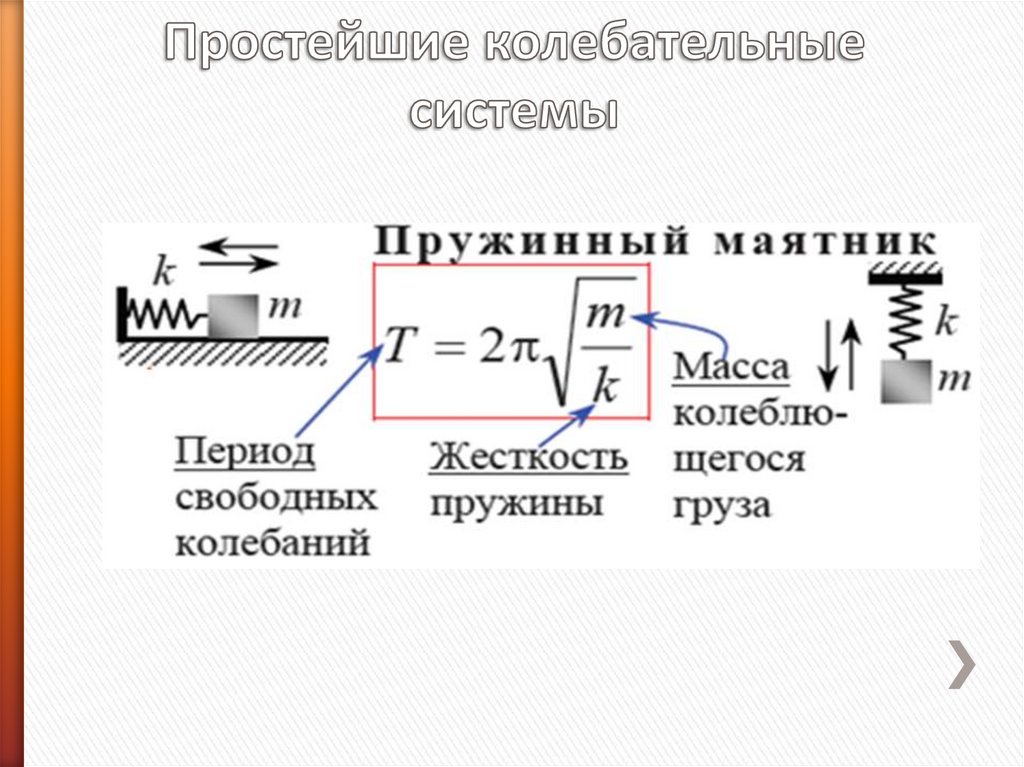
13.

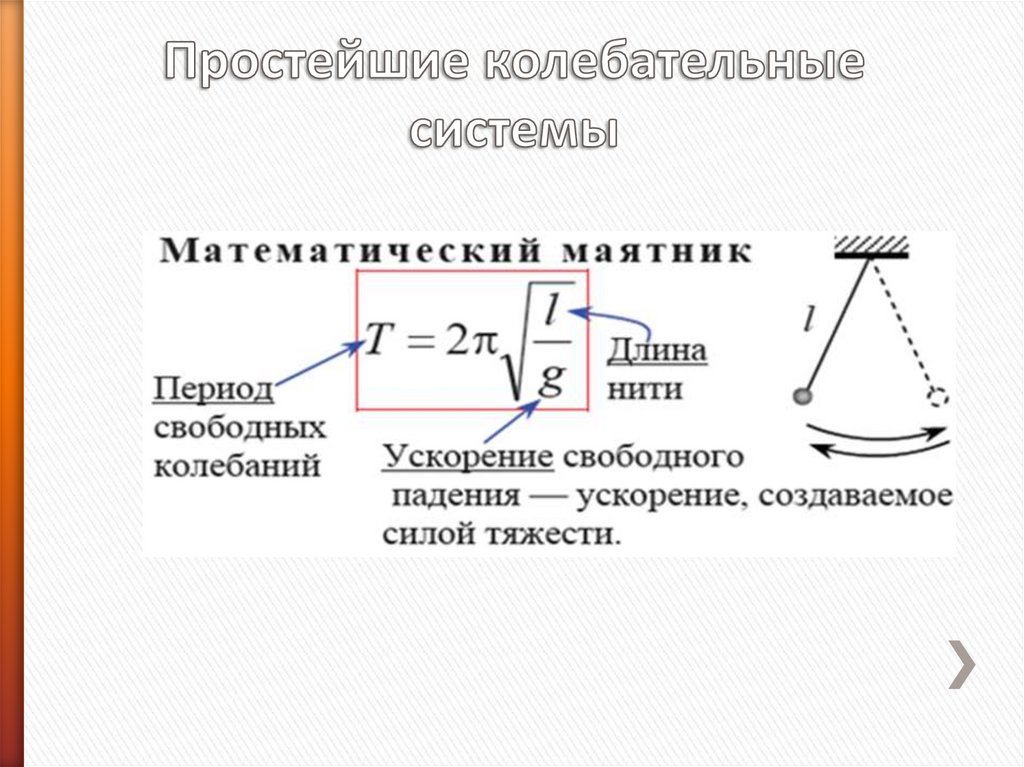
14.

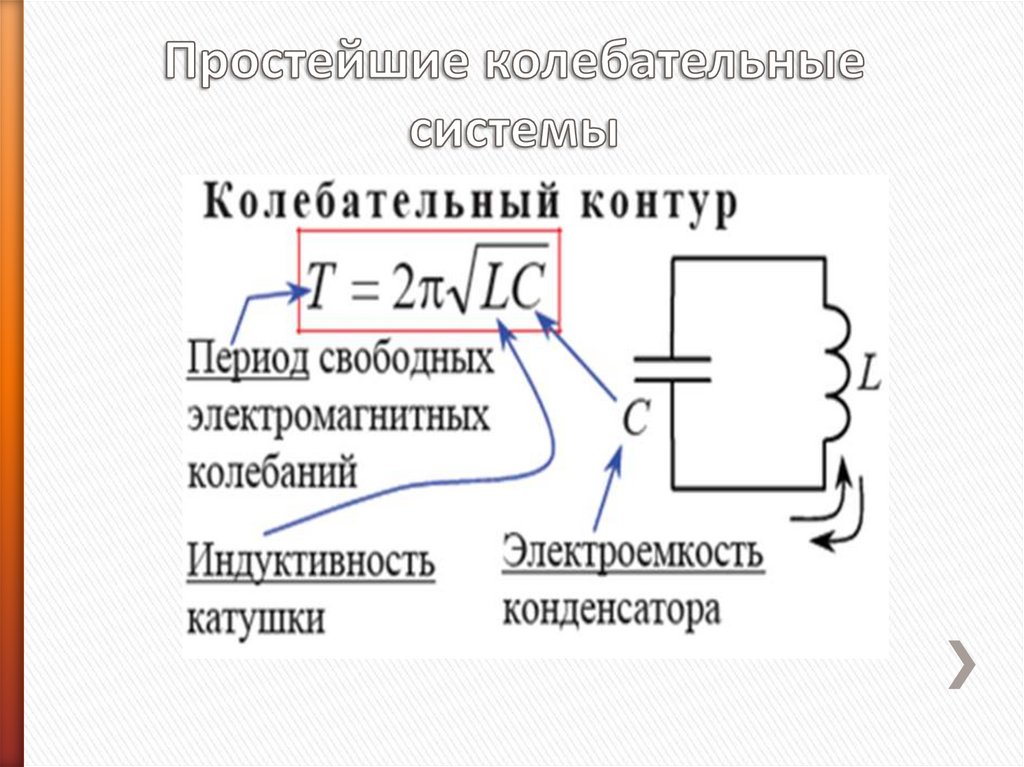
15.

16.

» В работе использованы опорные конспекты
Котова В.Е.
WWW.vkotov.narod.ru