Числа Фибоначчи

1.

Муниципальное образовательное учреждение города
Новосибирска
«Средняя общеобразовательная Школа №196»
Числа Фибоначчи
Выполнил: Захаров Александр Сергеевич, ученик 5
«М» класса.
Руководитель проекта: Светлана Васильевна
Горбачёва, учитель математики.
Новосибирск 2019 год

2.

Цель проекта:
• Изучить последовательность чисел Фибоначчи
• Рассмотреть роль в природе и практическое
применение
• Рассмотреть примеры «золотого сечения» в
природе
Задачи проекта:
• Познакомиться с числами Фибоначчи и историей
их создания.
• Рассмотреть закономерность чисел Фибоначчи.
• Изучить числовой ряд Фибоначчи

3.

Содержание
1. Леонардо Пизанский (Фибоначчи).
2. Последовательность Фибоначчи и ее свойства.
3. Спираль Фибоначчи и «Золотое сечение».
4. Пропорции Фибоначчи:
- в природе
- в архитектуре
- в космосе
5. Актуальность
6. Выводы.
7. Список используемой литературы.

4.

Первый крупный математик
средневековой Европы
( около 1170 – около 1250 гг.)
г.Пиза, в семье дипломата

5.

В молодости часто бывал в Алжире. Изучал
там математику у арабских учителей
Позже посетил Египет, Сирию, Византию,
Сицилию. Везде изучал труды математиков
По арабским переводам ознакомился с
достижениями античных и индийских
математиков
На основе усвоенных им знаний Фибоначчи
написал ряд выдающихся математических
трактатов

6.

Числа Фибоначчи
Числа Фибоначчи – элементы числовой последовательности
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …
в которой каждое последующее число, начиная с третьего,
равно сумме двух предыдущих чисел.
Эта последовательность была известна ещё в древней Индии,
где она применялась в метрических науках

7.

1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377,…
Каждое третье число чётное, каждое четвёртое
делится на 3, каждое пятое - на 5, каждое пятнадцатое
– на10
Невозможно построить треугольник, сторонами
которого являются числа ряда Фибоначчи (никакое
число ряда не может повторяться дважды)

8.

Прямоугольник с шириной и длиной равными двум соседним
числам Фибоначчи называют «золотым» прямоугольником

9.

Если разбивать его на более мелкие «золотые» прямоугольники и
разделить каждый из них дугой, то система приобретет форму
спирали, у которой есть начало, но нет конца

10.

Пропорции Фибоначчи в природе
Еще немецкий поэт Гёте подчеркивал
тенденцию природы к спиральности.
Спираль видна в ананасах, кактусах и т.д.
Паук плетет паутину спиралеобразно.
Спиралью закручивается ураган.
Чешуйки на поверхности сосновой шишки
расположены строго закономерно - по двум
спиралям, которые пересекаются
приблизительно под прямым углом. Число
таких спиралей у сосновых шишек равно 8
и 13 или 13 и 21.
Расстояние между листьями (или ветками
на стволе растения) относятся примерно как
числа Фибоначчи.

11.

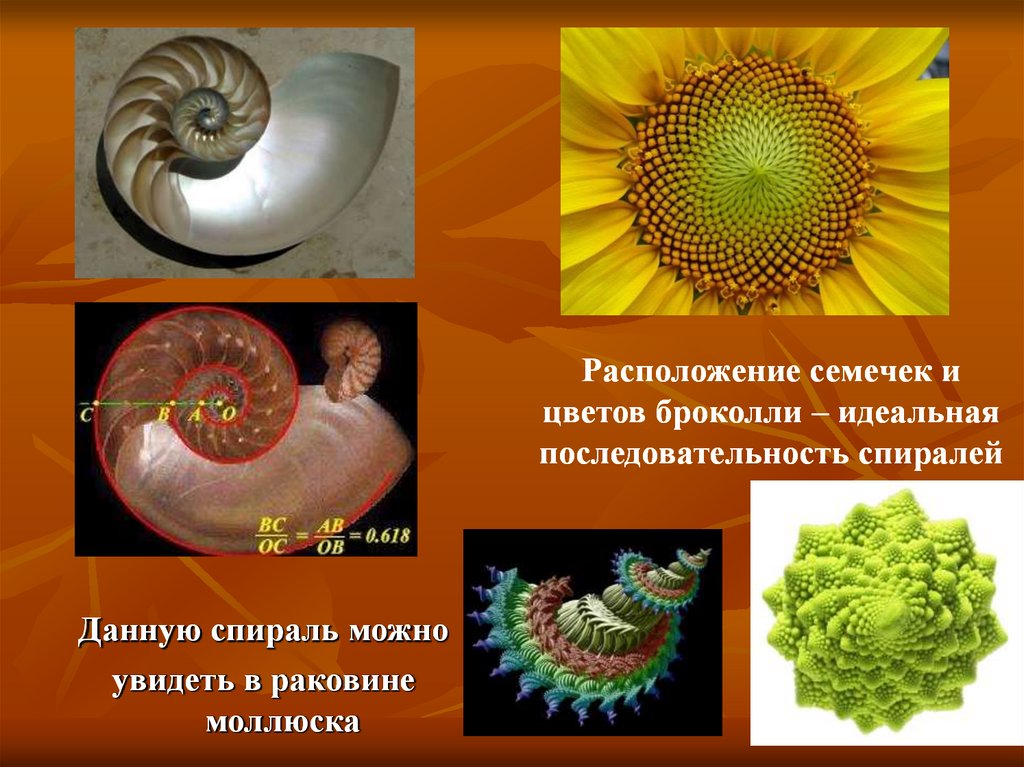
Расположение семечек и
цветов броколли – идеальная
последовательность спиралей
Данную спираль можно
увидеть в раковине
моллюска

12.

Пропорции Фибоначчи в архитектуре
Пирамиды в Гизе
Пирамиды Майя в Мексике
Во всех внешних и внутренних
пропорциях пирамид наблюдаются
соотношения чисел Фибоначчи

13.

Пропорции Фибоначчи в космосе
Рукава многих спиралевидных галактик расположены в
соответствии с этой последовательностью

14.

Актуальность темы
И в настоящее время числа Фибоначчи и их производные имеют
огромное значение в машиностроении, экономике и часто используется
в менеджменте и маркетинге.
Суть его сводится к тому, что необходимым
условием наличия или начала процесса устойчивого эволюционного
развития сложной рыночной социально-экономической системы
является существование в ее структуре пропорций «золотого сечения».

15.

Выводы
В результате работы я познакомился с
числами Фибоначчи
Числа Фибоначчи – это красиво, серьёзно,
актуально
Числа Фибоначчи имеют различное
проявление в природе, архитектуре, космосе
При выполнении работы я убедился, что
природа сама творит красоту по законам
математики

16.

Литература
1. А. И. Маркушевич Возвратные последовательности. — Гос. Издательство
Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции
по математике) .
2. А. Н. Рудаков Числа Фибоначчи и простота числа 2127-1 //
Математическое Просвещение, третья серия. — 2000. — Т. 4.

17.

Приложение 1
Вот такую спираль Фибоначчи я собрал из детской
мозаики

18.

Спасибо
за
внимание!