Similar presentations:
Золотое сечение. Числа Фибоначчи
1. Итоговый проект по теме “Золотое сечение. Числа Фибоначчи”
СОСТ А ВИ Т Е ЛЬ : Б Р А Й Ц Е В СЕ Р Г Е Й ,УЧЕ НИК 9 Г К ЛАССА
НА У ЧНЫ Й Р У К ОВОД И ТЕЛЬ: К У П Ц ОВА
И . Н. , У ЧИ Т Е ЛЬ М А Т ЕМ АТИ КИ
2. Введение
Проблема: Теме “Золотое сечение” почти не уделяется внимание в школьной программе.Актуальность: Актуальность исследования обусловлена стремлением углублять
математические знания через выявление связи между многими точными и естественными
науками, представления о красоте, порядке и гармонии, бытовые и производственные
сферы жизни.
Гипотеза: Золотое сечение высшее проявление структурного и функционального
совершенства целого и его частей в искусстве, науке, технике и природе.
Цель: Раскрыть суть понятий “Золотое сечение” и “Последовательность Фибоначчи”.
Показать присутствие золотой пропорции вокруг нас. Экспериментальным путем показать
золотое сечение в человеческом теле и объектах архитектуры
Задачи: Введение понятий “Золотое сечение” и “Ряд Фибоначчи”. Демонстрация Золотой
пропорции вокруг нас. Изучение человеческого тела и объектов архитектуры на наличие
золотого сечения. Формирование математической грамотности учащихся.
3. Что такое золотое сечение?
Золотое сечение – это деление отрезка на 2 части, при которых отношение длины всегоотрезка относится к большей части также, как большая часть к меньшей и это отношение
равно 1,618. Обозначается буквой φ(Фи).
4. История появления понятия
Само понятие ввел древнегреческий математик Пифагор, а нынешнее название “Золотоесечение” предложил Леонардо Да Винчи, который уделял много времени изучению
данной пропорции.
Пифагор
Леонардо Да Винчи
5. Последовательность Фибоначчи
Ряд Фибоначчи – бесконечный числовой ряд, где каждый новый член равен сумме двухпредыдущих, т.е. 1,1,2,3,5,8,13 и так далее. Носит своё название в честь математика Леонардо
Пизанского, более известного как Фибоначчи. Эта последовательность связана с числом золотой
пропорции так, что частное двух соседних чисел с каждым разом приближается к золотому числу
Леонардо Фибоначчи
Золотая пропорция в ряду Фибоначчи
6. Задача на размножение кроликов
В изолированное место поместили пару кроликов, природа которых такова, что любаяпара кроликов производит на свет другую пару каждый месяц, начиная со второго месяца
своего существования. Сколько пар кроликов будет через год? (Ответ:233 пары). Решается с
помощью ряда Фибоначчи.
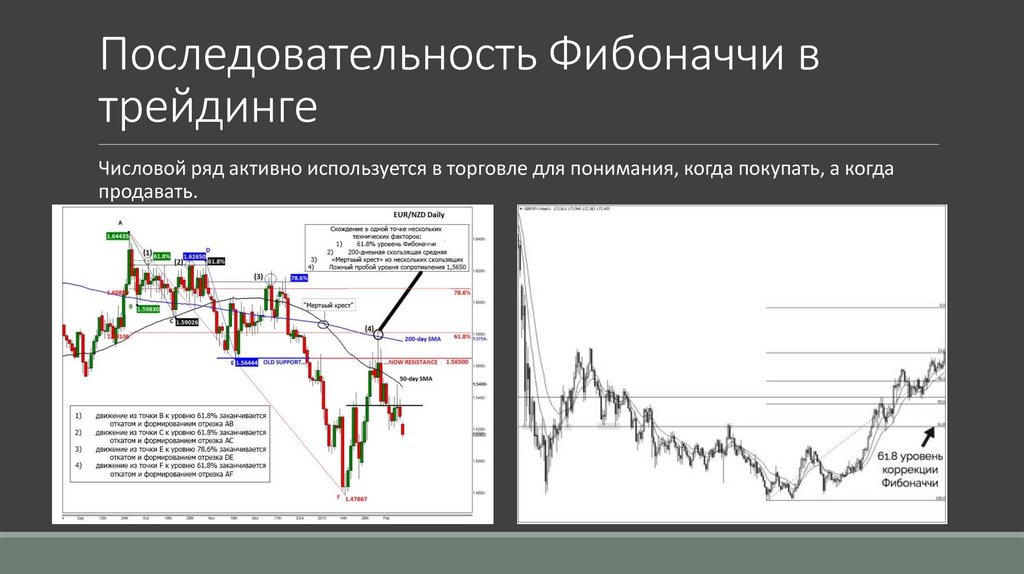
7. Последовательность Фибоначчи в трейдинге
Числовой ряд активно используется в торговле для понимания, когда покупать, а когдапродавать.
8. Золотая логарифмическая спираль
Золотая логарифмическая спираль – это логарифмическая спираль, коэффициент ростакоторой равен φ4, где φ — золотое сечение. Свое название эта спираль получила из-за
связи с последовательностью вложенных друг в друга прямоугольников с отношением
сторон, равным φ, которые принято называть золотыми. Золотую спираль можно как
вписать в систему таких прямоугольников, так и описать вокруг нее.
Золотая спираль в золотом прямоугольнике
Золотая спираль(Спираль Фибоначчи)
9. Золотое сечение в архитектуре
ПарфенонКалифорнийская инженерная школа
Храм Василия Блаженного
10. Золотое сечение в живописи
Мона ЛизаАфинская школа
Иоанн-креститель
11. Золотое сечение в музыке
Золотое сечение в музыке отражает человеческое восприятие временных пропорций. Насекунду, номер которой есть в ряду Фибоначчи может приходиться кульминация или
самый тихий момент. Также имеет место быть в создании музыкальных инструментов
12. Исследование
Человек – лучшее творение природы и он своими руками строит невероятной красотыархитектурные сооружения. Я собрал информацию о размерах частей тела своих
родственников и некоторых друзей, а также нашел информацию о размерах красивых
российских зданий, чтобы проверить: Есть ли там золотое сечение.
13. Часть 1. Измерение человека
ИмяА1(см)
Б1(см)
В1
Брайцева Алия
167,4
103,5
1,617
Брайцев Дмитрий
177,1
108,1
1,645
Брайцев Юрий
169.7
106,5
1,593
Брайцева Ирина
175,2
105,7
1,658
Брайцева Анна
156,8
99,0
1,584
Босомыкин Даниил
184,0
114,2
1,611
Дима И
183,8
113,6
1,618!
Тимур Фазылов
187,6
119,2
1,574
Илья Панченко
162,3
97,9
1,658
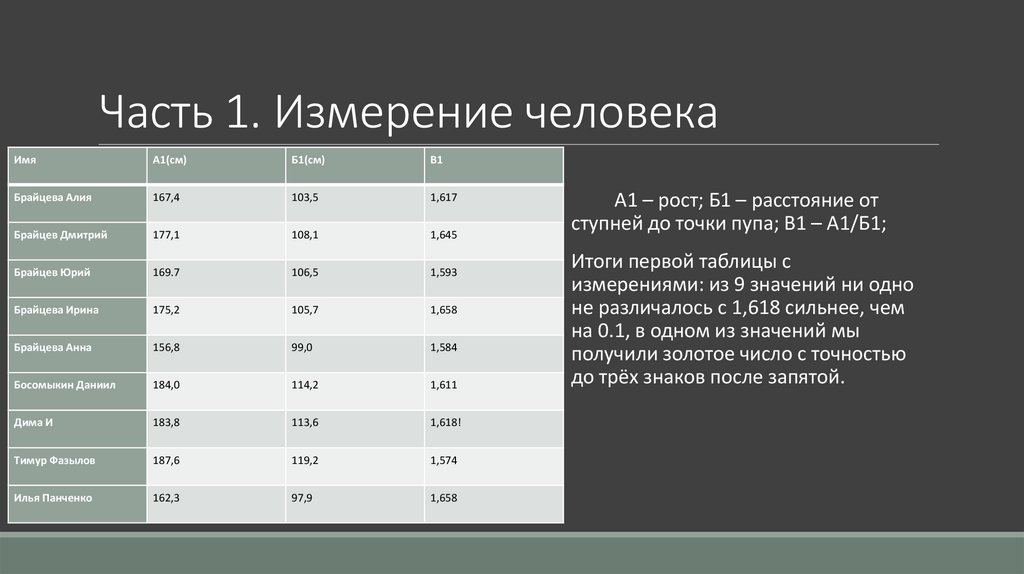
А1 – рост; Б1 – расстояние от
ступней до точки пупа; В1 – А1/Б1;
Итоги первой таблицы с
измерениями: из 9 значений ни одно
не различалось с 1,618 сильнее, чем
на 0.1, в одном из значений мы
получили золотое число с точностью
до трёх знаков после запятой.
14. Часть 1. Измерение человека
ИмяА2(см)
Б2(см)
В2
Брайцева Алия
41
32
1,281
Брайцев Дмитрий
44
34
1,294
Брайцев Юрий
42
30
1,400
Брайцева Ирина
43
34
1,264
Брайцева Анна
38
27
1,407
Босомыкин Даниил
46
35
1,314
Дима И
46
33
1,393
Тимур Фазылов
47
38
1,236
Илья Панченко
41
34
1,205
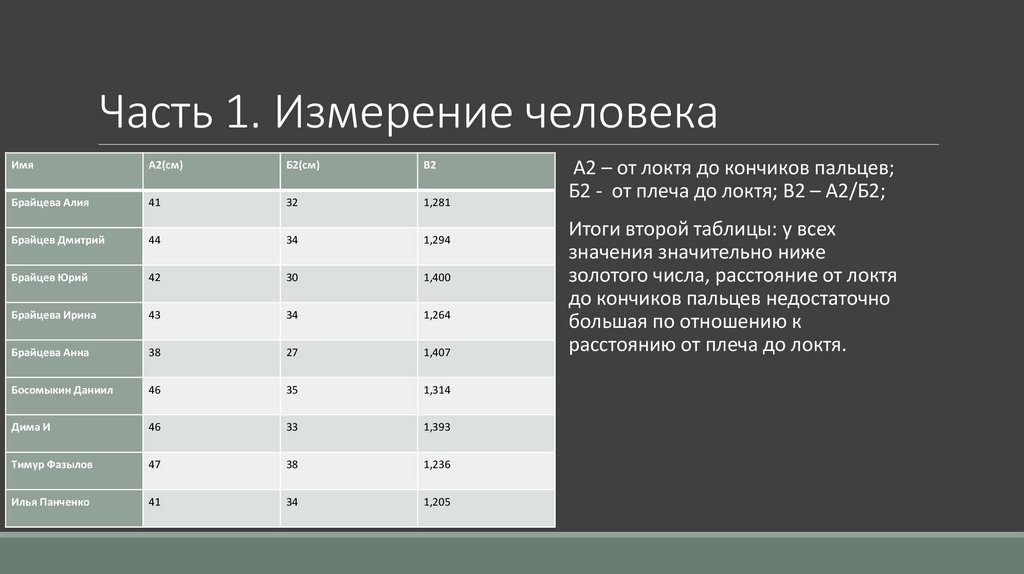
А2 – от локтя до кончиков пальцев;
Б2 - от плеча до локтя; В2 – А2/Б2;
Итоги второй таблицы: у всех
значения значительно ниже
золотого числа, расстояние от локтя
до кончиков пальцев недостаточно
большая по отношению к
расстоянию от плеча до локтя.
15. Часть 1. Измерение человека
ИмяА3(см)
Б3(см)
В3
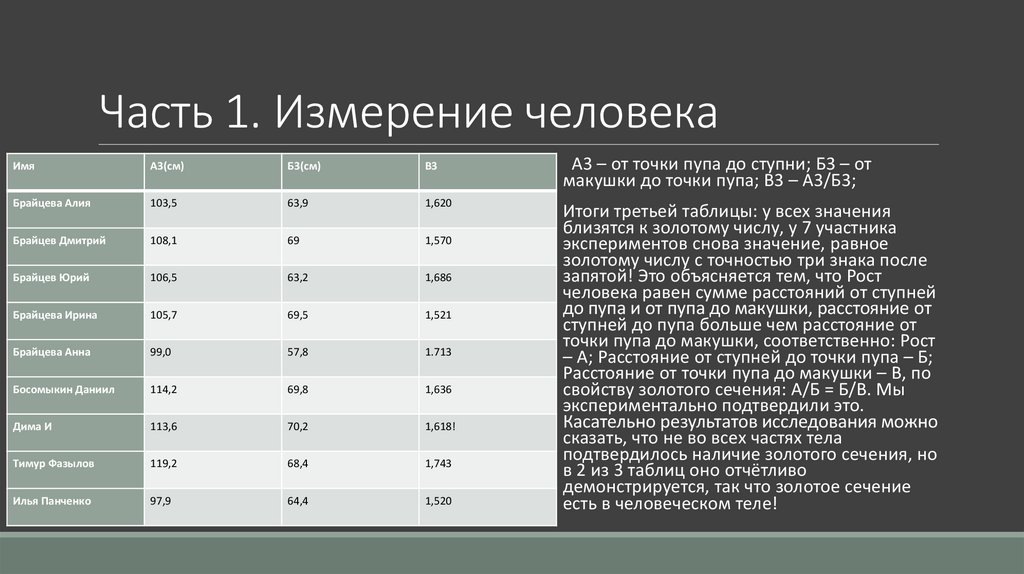
А3 – от точки пупа до ступни; Б3 – от
макушки до точки пупа; В3 – А3/Б3;
Брайцева Алия
103,5
63,9
1,620
Брайцев Дмитрий
108,1
69
1,570
Брайцев Юрий
106,5
63,2
1,686
Брайцева Ирина
105,7
69,5
1,521
Брайцева Анна
99,0
57,8
1.713
Босомыкин Даниил
114,2
69,8
1,636
Дима И
113,6
70,2
1,618!
Тимур Фазылов
119,2
68,4
1,743
Илья Панченко
97,9
64,4
1,520
Итоги третьей таблицы: у всех значения
близятся к золотому числу, у 7 участника
экспериментов снова значение, равное
золотому числу с точностью три знака после
запятой! Это объясняется тем, что Рост
человека равен сумме расстояний от ступней
до пупа и от пупа до макушки, расстояние от
ступней до пупа больше чем расстояние от
точки пупа до макушки, соответственно: Рост
– А; Расстояние от ступней до точки пупа – Б;
Расстояние от точки пупа до макушки – В, по
свойству золотого сечения: А/Б = Б/В. Мы
экспериментально подтвердили это.
Касательно результатов исследования можно
сказать, что не во всех частях тела
подтвердилось наличие золотого сечения, но
в 2 из 3 таблиц оно отчётливо
демонстрируется, так что золотое сечение
есть в человеческом теле!
16. Часть 2. Измерение зданий
1. Исаакиевский собор(Санкт-Петербург)Собор строился в стиле классицизма, и в нём прослеживаются черты неоренесанса.
В строении собора виден равнобедренный
треугольник. Отношение основной части к длине
купола равна 247/153=1,614. Основная часть
с колоннами имеет соотношение сторон 400/247
=1,619. Золотое сечение есть в этом соборе.
17. Часть 2. Измерение зданий
2. Дом Советов(Санкт-Петербург)Высота всего здания – 178м, основной его части – 118м, поделив, получим 1,508≈золотому
сечению. Вершина Золотого равнобедренного треугольника совпадает с вершиной здания,
а его стороны проходят через верхние точки главного входа. Прямоугольный золотой
треугольник образован вершинами в наивысшие точки здания и в конце бокового крыла
внутри. Золотая пропорция также прослеживается.
18. Заключение
Золотое сечение – воистину можно назвать математическим сокровищем. Оноприсутствует в большом количестве, если не во всех сферах нашей жизни. Понятие золотое
сечение заложено человеку еще с ранних лет жизни, так как красивые здания, где
присутствует золотая пропорция всегда привлекают наш глаз. Мы познакомились с этим
понятием, узнали, как оно зарождалось, где оно находится ежедневно вокруг нас, узнали
про последовательность Фибоначчи и её непосредственную связь с ЗС. Провели своё
исследование, проверили, есть ли золотое сечение в человеческом теле, убедились, что
оно действительно имеет место быть там. Нашли золотую пропорцию в красивых
архитектурных сооружениях и убедились, что архитектура и ЗС также связаны. Теперь мы
знаем, что из себя представляет золотое сечение и можем применить полученные знания
на практике, находя его вокруг нас. Цель проекта считаю выполненной.














 mathematics
mathematics








