Обоснование. Задание №1

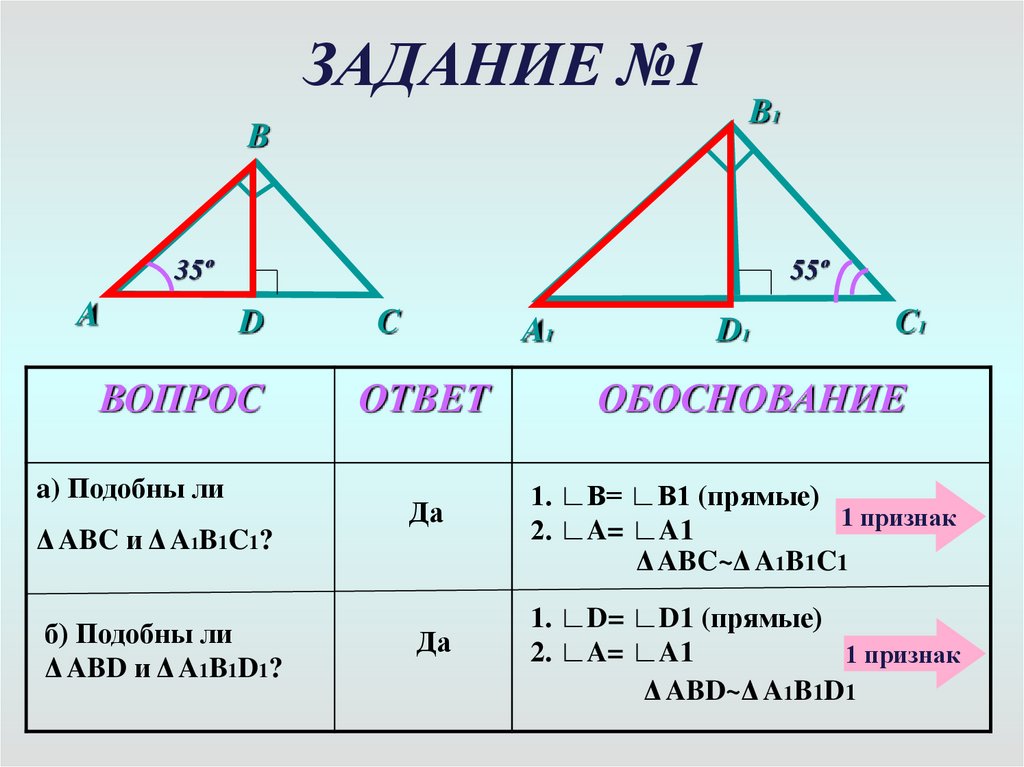
1. ЗАДАНИЕ №1

B1
B
35º
A
55º
D
ВОПРОС
a) Подобны ли
Δ ABC и Δ A1B1C1?
б) Подобны ли
Δ ABD и Δ A1B1D1?
C
A1
ОТВЕТ
Да
Да
D1
C1
ОБОСНОВАНИЕ
1. ∟В= ∟В1 (прямые)
1 признак
2. ∟A= ∟A1
Δ ABC~Δ A1B1C1
1. ∟D= ∟D1 (прямые)
2. ∟A= ∟A1
1 признак
Δ ABD~Δ A1B1D1

2. ЗАДАНИЕ №2

ВОПРОС
ОТВЕТ
ОБОСНОВАНИЕ
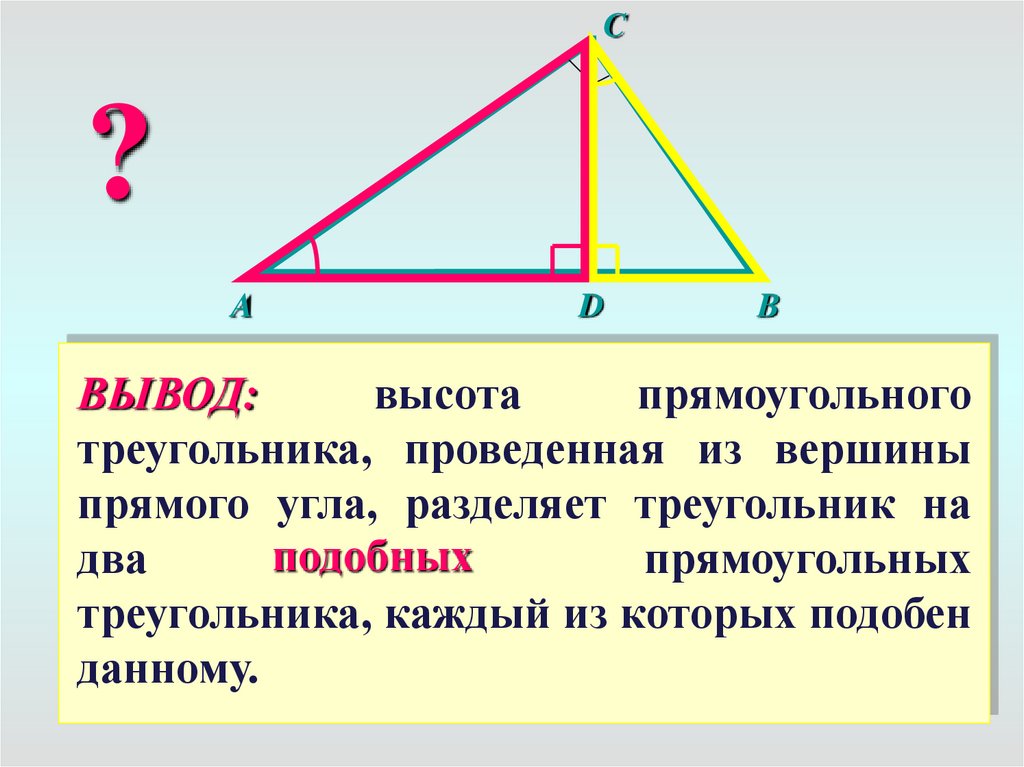
ВЫВОД:
высота
прямоугольного
треугольника,
проведенная
из
вершины
1.
∟D=
∟В
(прямые)
a) Подобны ли
Да
1 признaк
2. ∟A треугольник
– общий
прямого
угла,
разделяет
на
Δ ADB и Δ ABC?
AВС
два
прямоугольных Δ ADB~Δ
треугольника,
б) Подобны ли
1. ∟D= ∟В
(прямые)
Да
каждый из которых
подобен
данному.
1 признaк
Δ BDC и Δ ABC?
2. ∟C – общий
Δ BDC~Δ AВС

3.

C
?
A
D
B
ВЫВОД:
высота
прямоугольного
треугольника,
проведенная
из
вершины
1. ∟ADС= ∟CDB (т.к. СD-высота)
1 признак
прямого угла, разделяет треугольник
на
2. ∟СAD= ∟BCD (т.к. Δ BDC~Δ ABC)
подобных
два
прямоугольных
Δ ADB~Δ CDB
треугольника, каждый из которых подобен
данному.

4.

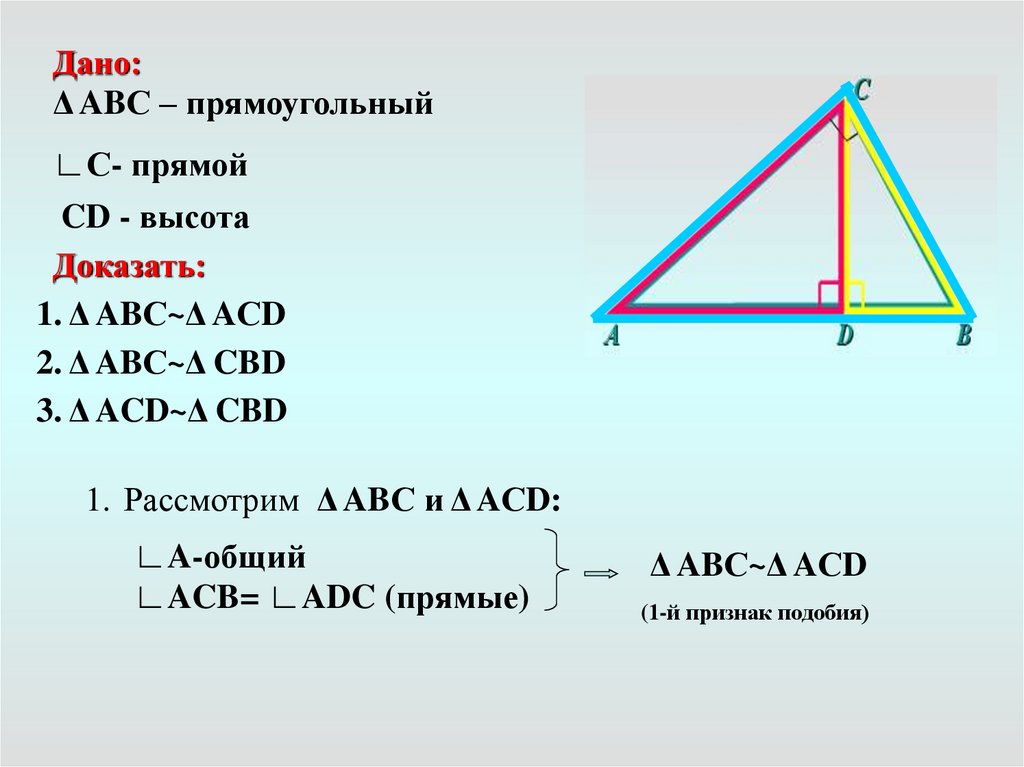
Дано:
Δ ABС – прямоугольный
∟С- прямой
CD - высота
Доказать:
1. Δ ABС~Δ AСD
2. Δ ABС~Δ CBD
3. Δ ACD~Δ CBD
1. Рассмотрим Δ ABС и Δ AСD:
∟A-общий
∟ACB= ∟ADC (прямые)
Δ ABС~Δ AСD
(1-й признак подобия)

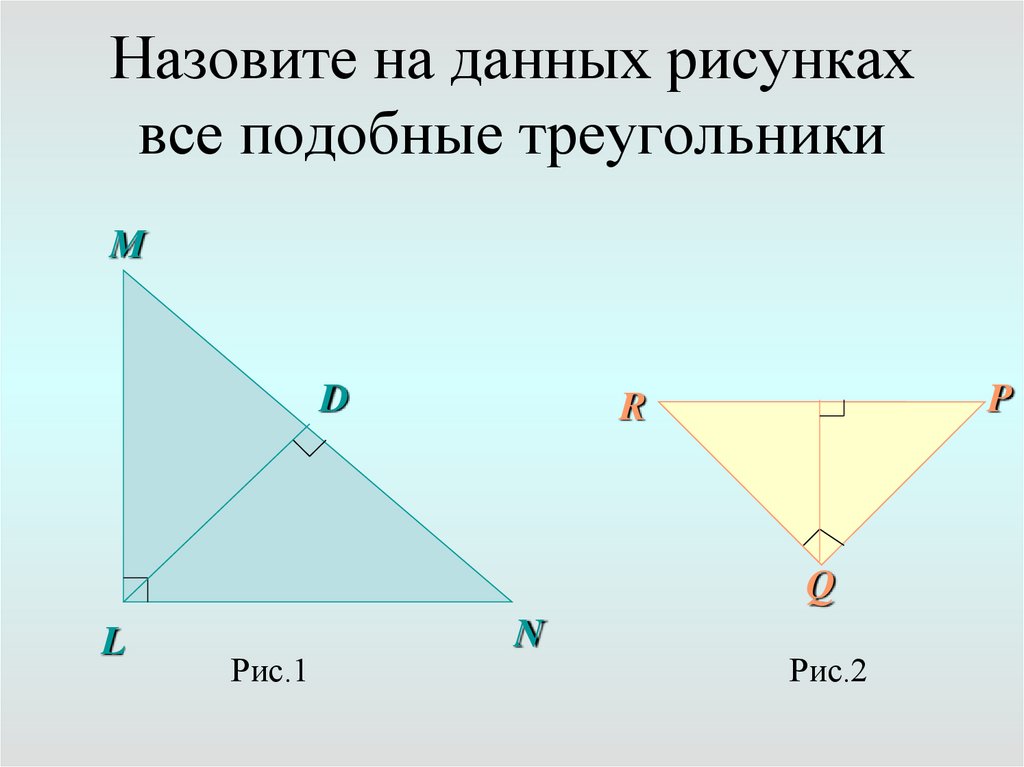
5. Назовите на данных рисунках все подобные треугольники

M
D
P
R
Q
L
Рис.1
N
Рис.2

6. Внимание!

Определение. Отрезок XY называется
средним
пропорциональным
(средним геометрическим) между
отрезками AB и CD, если
XY
AB CD

7.

№1. Найдите длину среднего пропорционального
отрезков MN и KP, если MN=9см, KP=16см
XY MN KP 9 16
№1. Найдите длину отрезка AB, если среднее
пропорциональное отрезков AB и СD равно 90см и
CD=100 см
XY AB CD
XY 2 AB CD
XY 2 90 90
AB
81
CD
100

8.

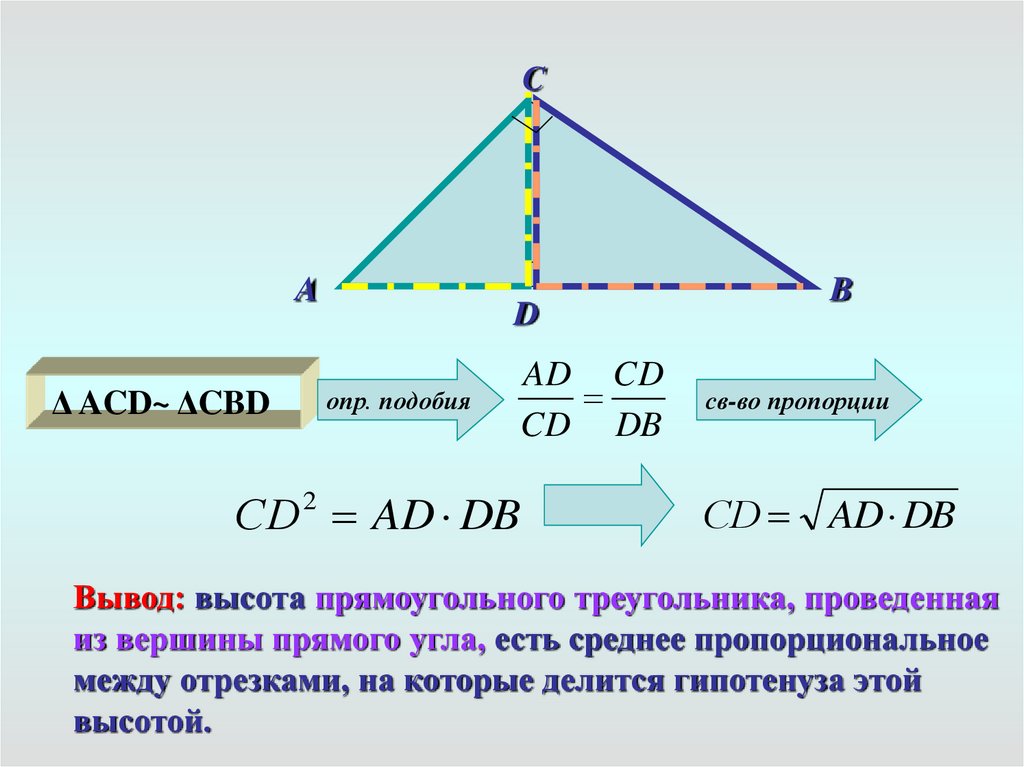
C
A
Δ ACD~ ΔCBD
D
опр. подобия
AD CD
CD DB
СD 2 AD DB
B
св-во пропорции
СD AD DB
Вывод: высота прямоугольного треугольника, проведенная
из вершины прямого угла, есть среднее пропорциональное
между отрезками, на которые делится гипотенуза этой
высотой.

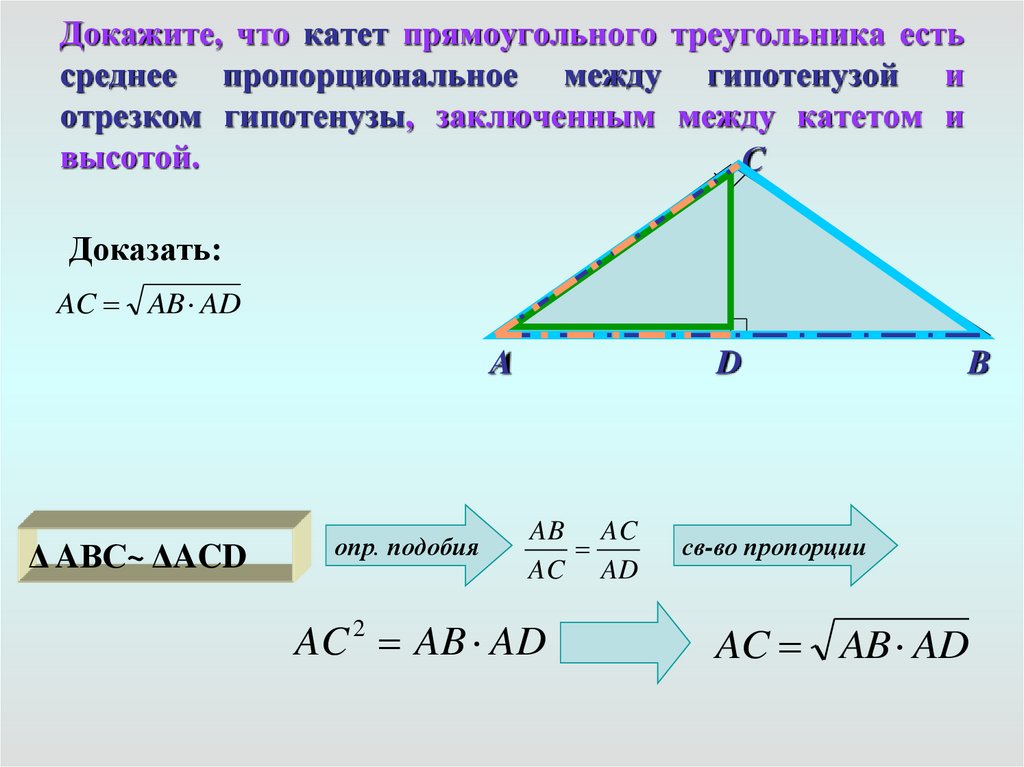
9. Докажите, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,

заключенным между катетом и
высотой.
С
Доказать:
AC AB AD
A
Δ AВС~ ΔACD
опр. подобия
D
AB AC
AC AD
AC AB AD
2
B
св-во пропорции
AC AB AD

10.

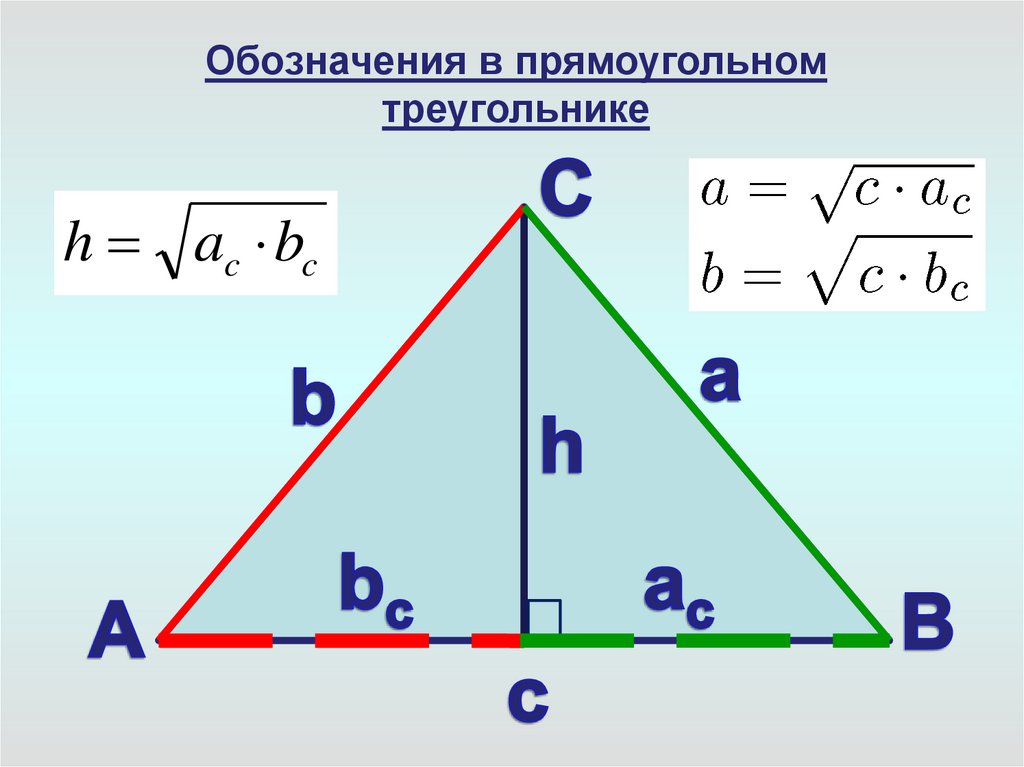
Обозначения в прямоугольном
треугольнике
h ac bc