Similar presentations:
Планиметрия и основные фигуры
1.
2.
3.
4.
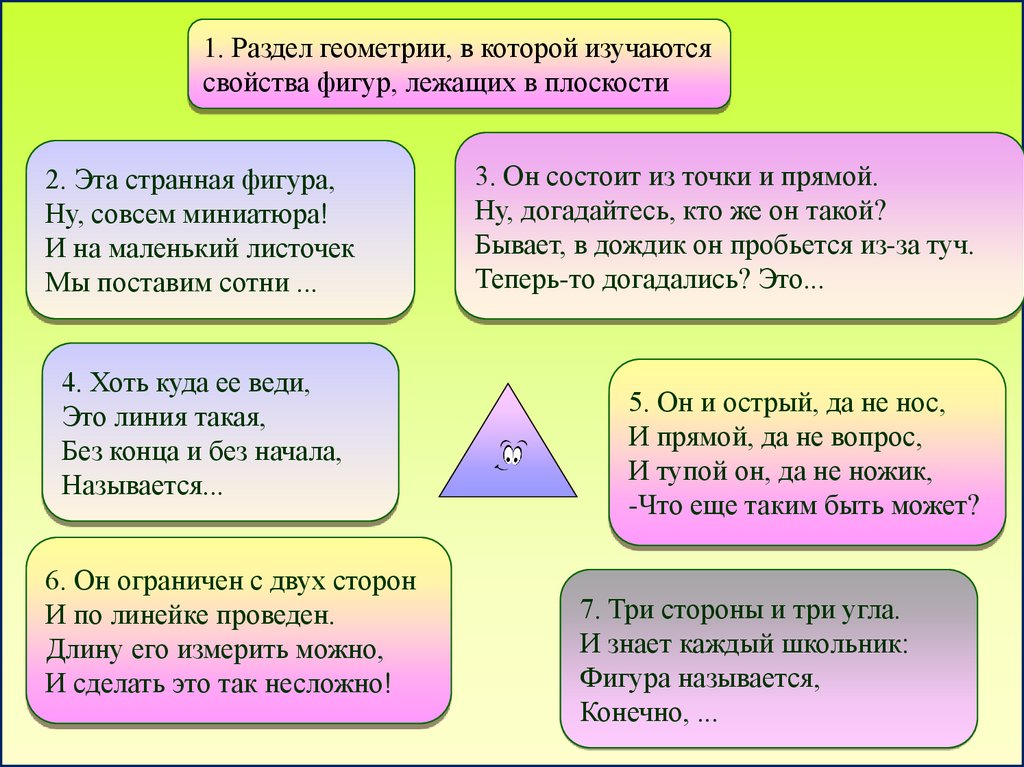
1. Раздел геометрии, в которой изучаютсясвойства фигур, лежащих в плоскости
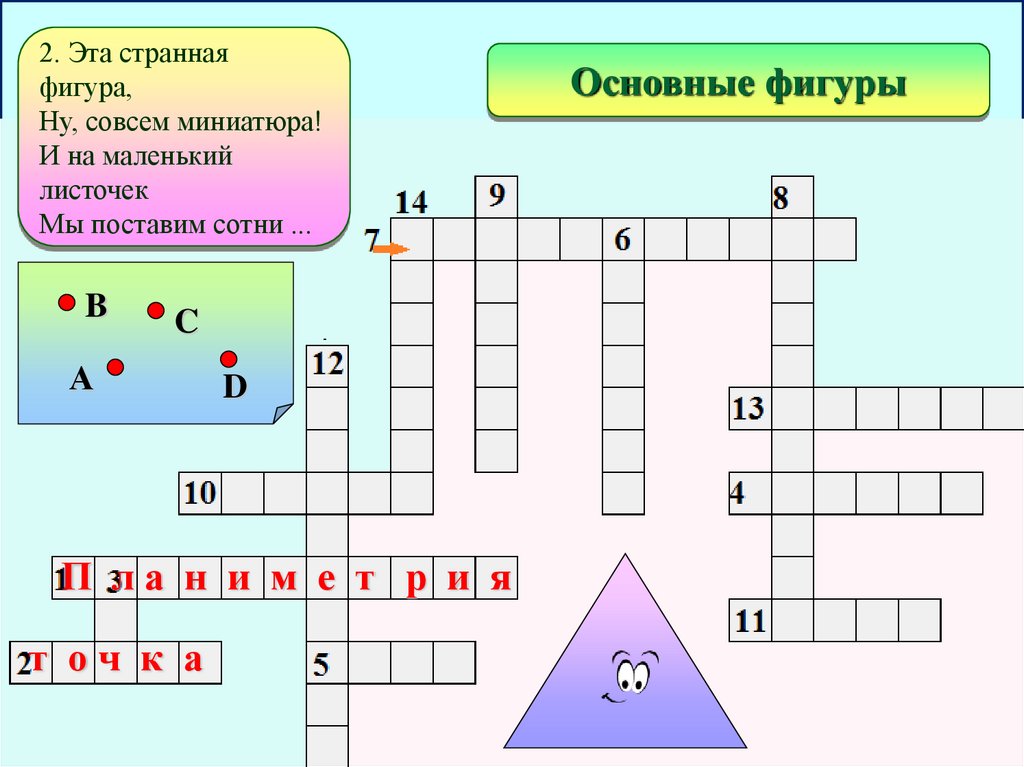
2. Эта странная фигура,
Ну, совсем миниатюра!
И на маленький листочек
Мы поставим сотни ...
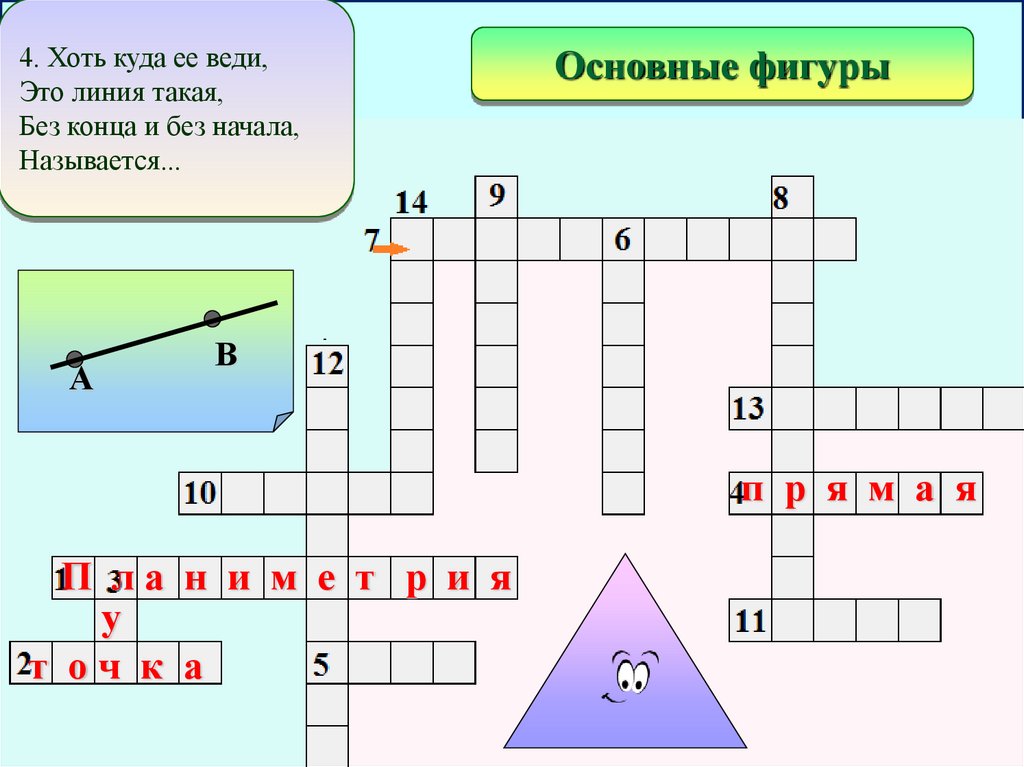
4. Хоть куда ее веди,
Это линия такая,
Без конца и без начала,
Называется...
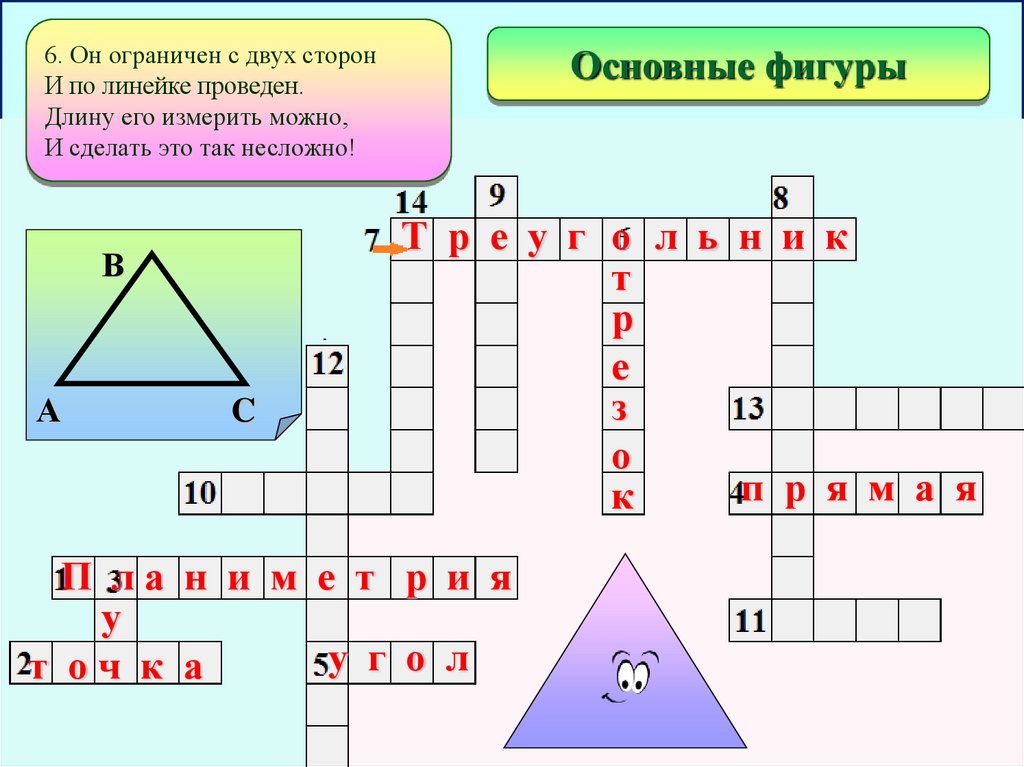
6. Он ограничен с двух сторон
И по линейке проведен.
Длину его измерить можно,
И сделать это так несложно!
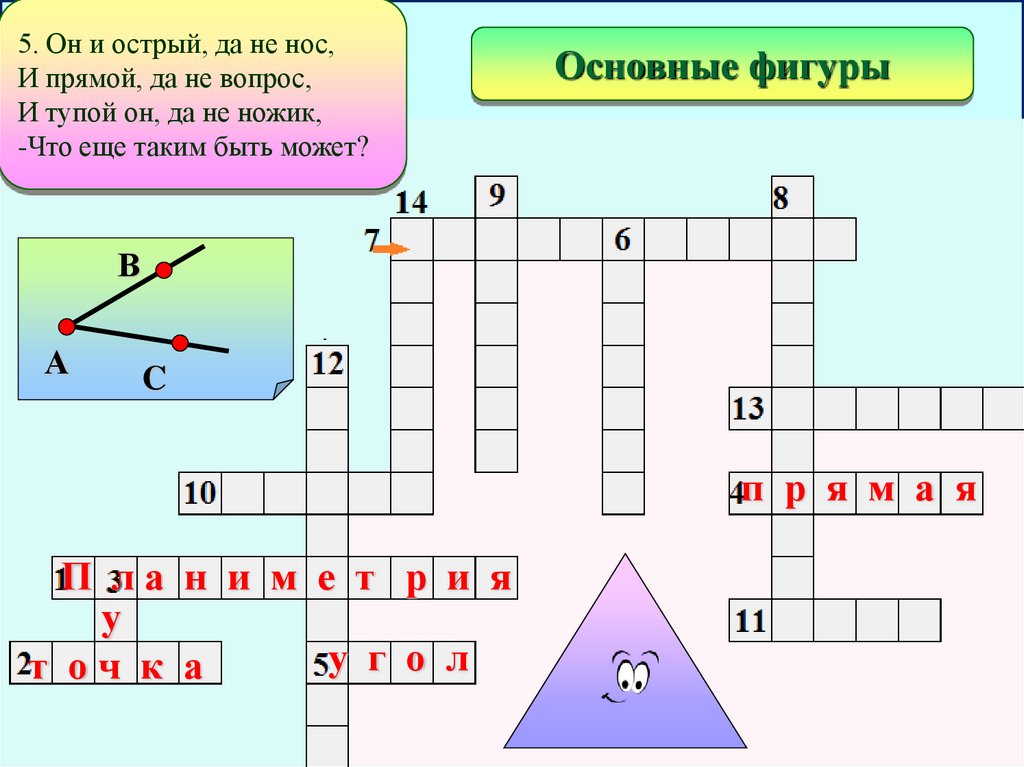
3. Он состоит из точки и прямой.
Ну, догадайтесь, кто же он такой?
Бывает, в дождик он пробьется из-за туч.
Теперь-то догадались? Это...
5. Он и острый, да не нос,
И прямой, да не вопрос,
И тупой он, да не ножик,
-Что еще таким быть может?
7. Три стороны и три угла.
И знает каждый школьник:
Фигура называется,
Конечно, ...
5.
ПланиметрияП ла н и м е т р и я
Раздел геометрии, в которой изучаются
свойства фигур, лежащих в плоскости
6.
2. Эта страннаяфигура,
Ну, совсем миниатюра!
И на маленький
листочек
Мы поставим сотни ...
B
C
А
D
П ла н и м е т р и я
т оч к а
Основные фигуры
7.
3. Он состоит из точки и прямой.Ну, догадайтесь, кто же он такой?
Бывает, в дождик он пробьется из-за туч.
Теперь-то догадались? Это...
B
А
П ла н и м е т р и я
у
т оч к а
Основные фигуры
8.
4. Хоть куда ее веди,Это линия такая,
Без конца и без начала,
Называется...
А
Основные фигуры
В
п р я м а я
П ла н и м е т р и я
у
т оч к а
9.
5. Он и острый, да не нос,И прямой, да не вопрос,
И тупой он, да не ножик,
-Что еще таким быть может?
Основные фигуры
В
А
C
п р я м а я
П ла н и м е т р и я
у
у г о л
т оч к а
10.
6. Он ограничен с двух сторонИ по линейке проведен.
Длину его измерить можно,
И сделать это так несложно!
В
А
П ла н и м е т р и я
у
у г о л
т оч к а
Основные фигуры
о
т
р
е
з
о
к
п р я м а я
11.
6. Он ограничен с двух сторонИ по линейке проведен.
Длину его измерить можно,
И сделать это так несложно!
В
А
C
Основные фигуры
Т р е у г о л ь н и к
т
р
е
з
о
п р я м а я
к
П ла н и м е т р и я
у
у г о л
т оч к а
12.
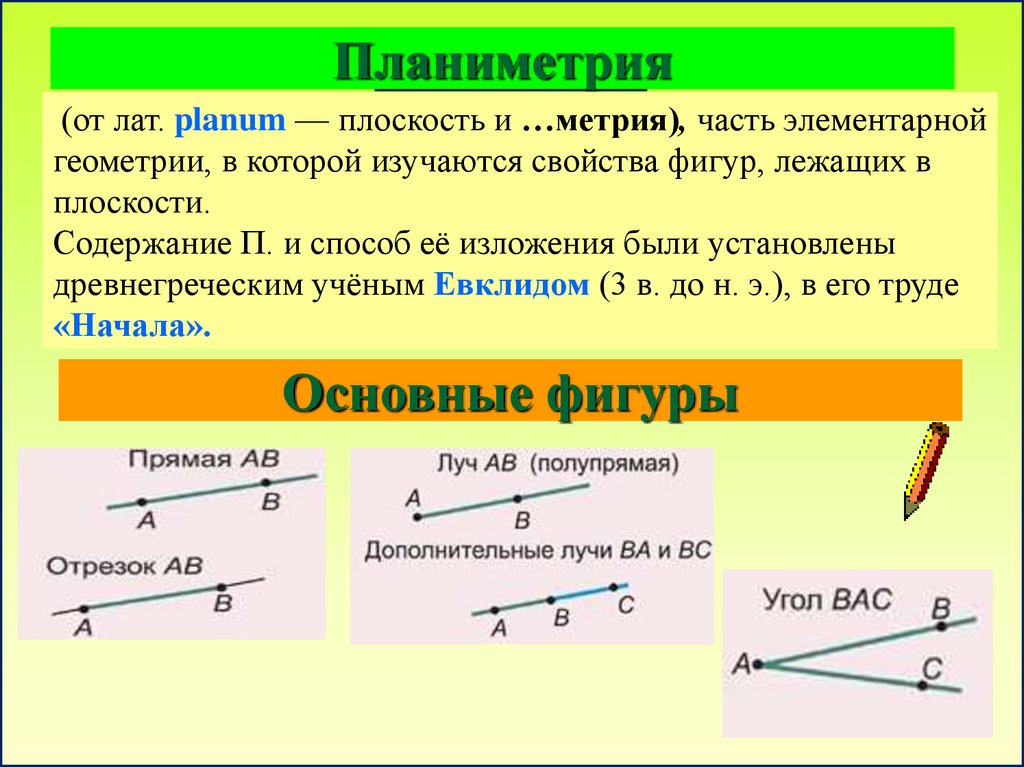
Планиметрия__________
(от лат. planum — плоскость и …метрия), часть элементарной
геометрии, в которой изучаются свойства фигур, лежащих в
плоскости.
Содержание П. и способ её изложения были установлены
древнегреческим учёным Евклидом (3 в. до н. э.), в его труде
«Начала».
Основные фигуры
13.
Смежные______ ____
углы
AOB + BOC = 1800
Вертикальные углы
AOB = COD
AOD = BOC
14.
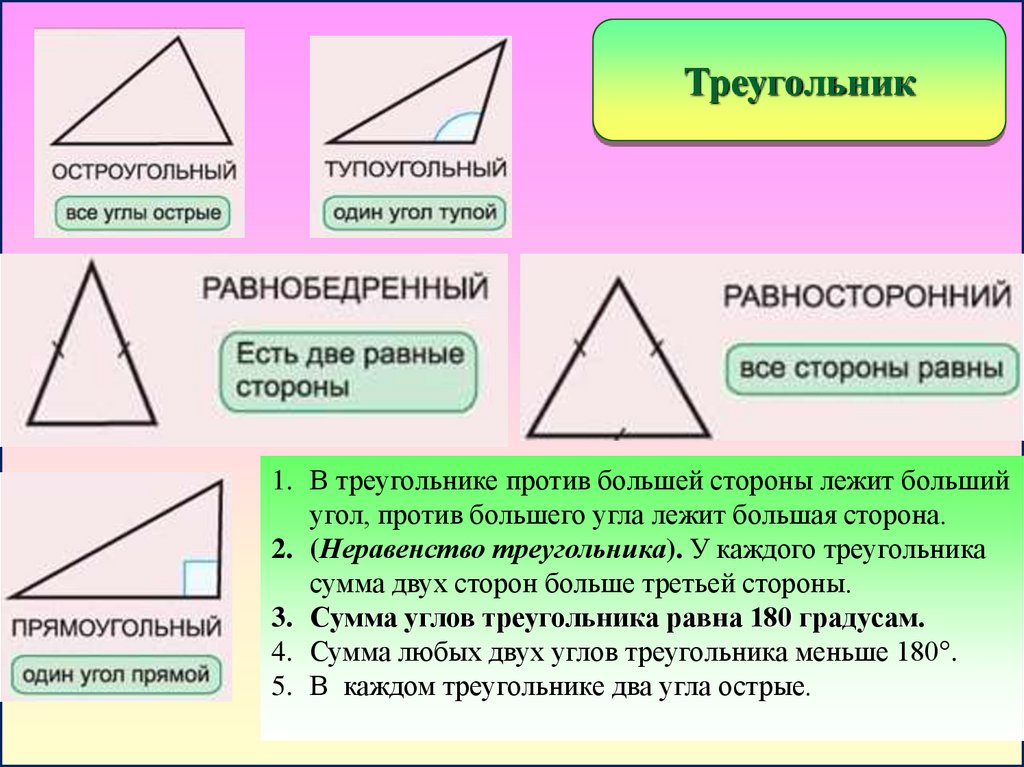
Треугольник1. В треугольнике против большей стороны лежит больший
угол, против большего угла лежит большая сторона.
2. (Неравенство треугольника). У каждого треугольника
сумма двух сторон больше третьей стороны.
3. Сумма углов треугольника равна 180 градусам.
4. Сумма любых двух углов треугольника меньше 180°.
5. В каждом треугольнике два угла острые.
15.
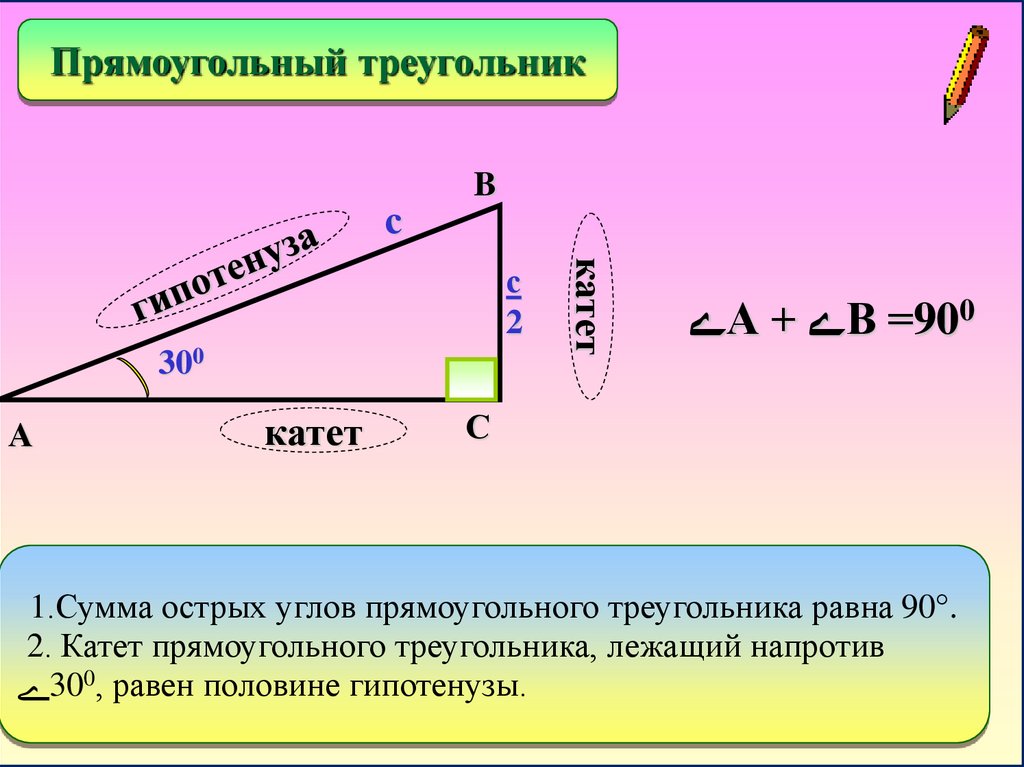
Прямоугольный треугольникс
B
300
А
катет
катет
с
2
А + В =900
С
1.Сумма острых углов прямоугольного треугольника равна 90°.
2. Катет прямоугольного треугольника, лежащий напротив
300, равен половине гипотенузы.
16.
Основные линии треугольника9. Медиана треугольника - это отрезок, который
связывает вершину треугольника с серединой одной из
сторон данного треугольника.
Биссектриса угла – это исходящий из вершины угла луч,
пролегающий между образующими сторонами и
разделяющий его пополам.
8. Биссектриса треугольника – это отрезок биссектрисы
угла треугольника, объединяющий его вершину с точкой на
противолежащем отрезке этого треугольника.
10. Высота треугольника – это перпендикуляр,
проведенный из вершины треугольника к
противоположной стороне
Средняя линия - отрезок, который соединяет две
стороны треугольника в их серединах.
17.
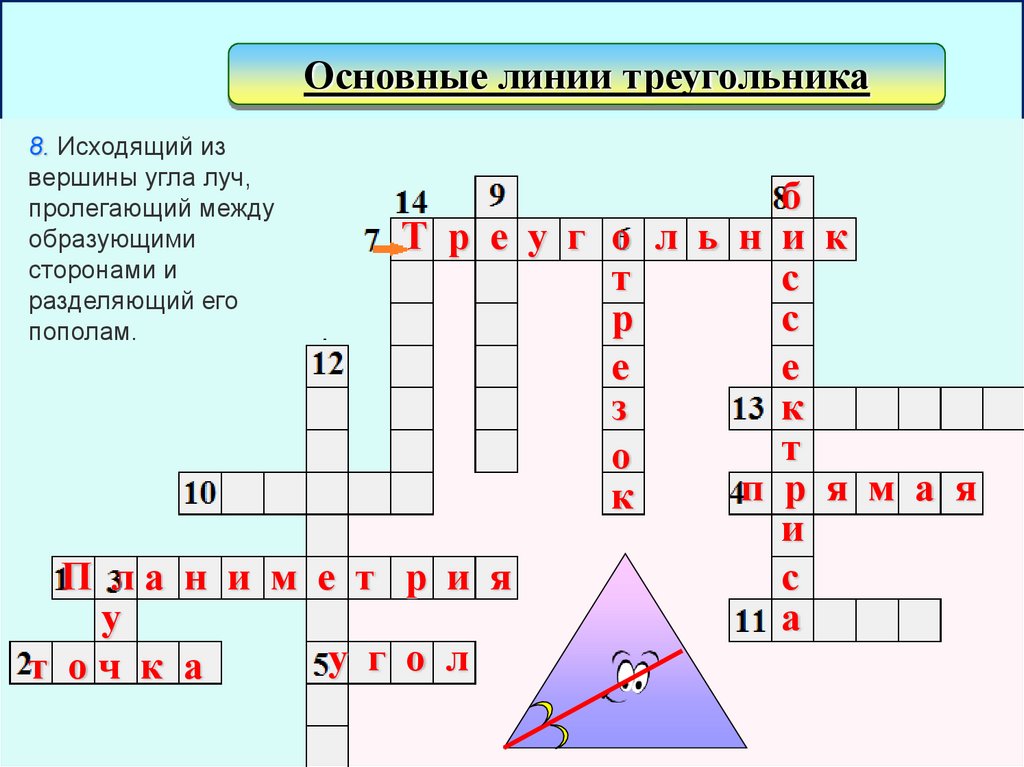
Основные линии треугольника8. Исходящий из
вершины угла луч,
пролегающий между
образующими
сторонами и
разделяющий его
пополам.
б
Т р е у г о л ь н и к
т
с
р
с
е
е
з
к
т
о
п р я м а я
к
и
П ла н и м е т р и я
с
у
а
у г о л
т оч к а
18.
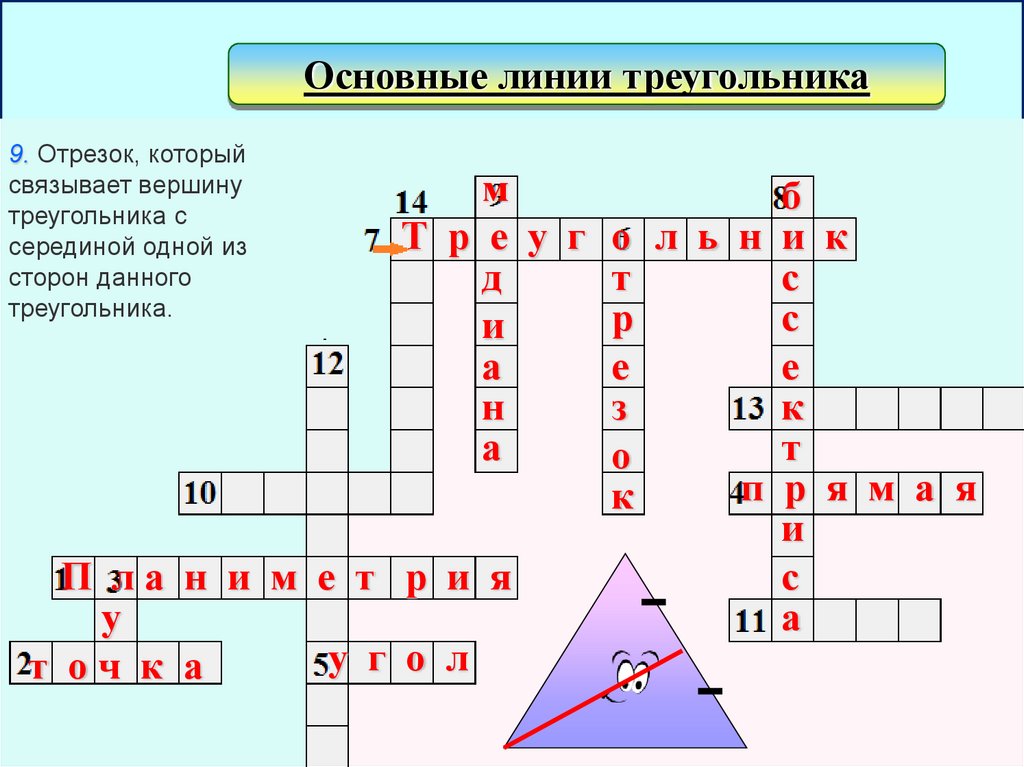
Основные линии треугольника9. Отрезок, который
связывает вершину
треугольника с
серединой одной из
сторон данного
треугольника.
м
Т р е у г о л ь н
д
т
р
и
а
е
н
з
а
о
п
к
П ла н и м е т р и я
у
у г о л
т оч к а
б
и к
с
с
е
к
т
р я м а я
и
с
а
19.
Основные линии треугольника10. перпендикуляр,
проведенный из
вершины треугольника
к противоположной
стороне
м
Т р е у г о л ь н
д
т
р
и
а
е
н
з
а
о
в ы с о т а
п
к
П ла н и м е т р и я
у
у г о л
т оч к а
б
и к
с
с
е
к
т
р я м а я
и
с
а
20.
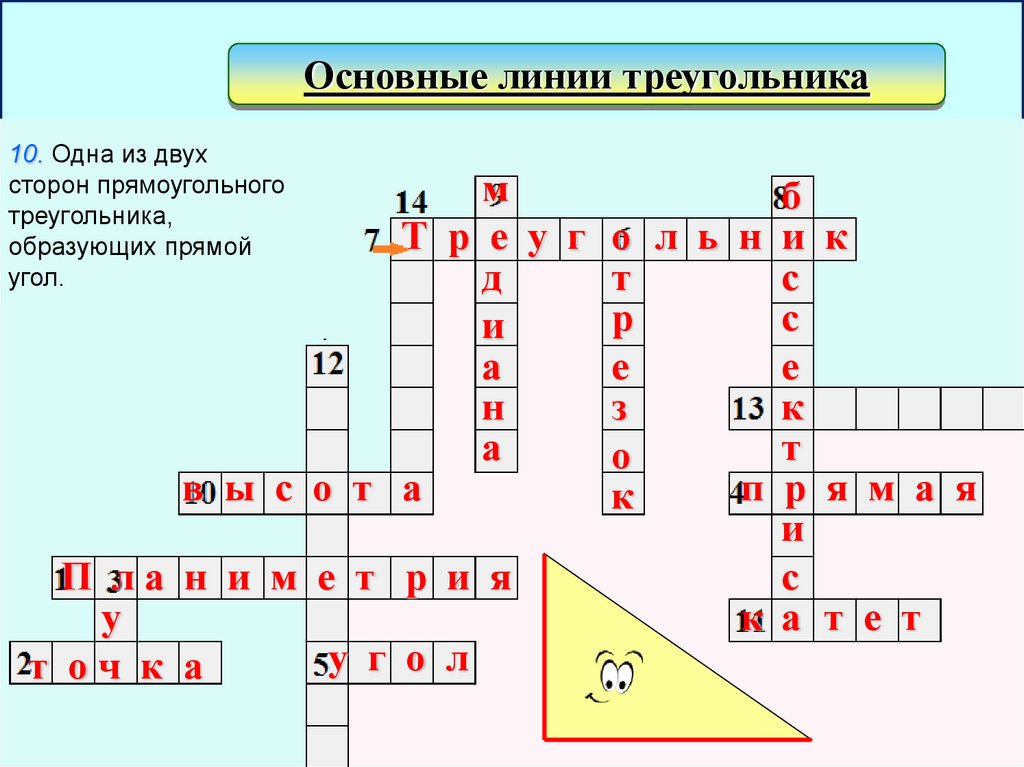
Основные линии треугольника10. Одна из двух
сторон прямоугольного
треугольника,
образующих прямой
угол.
м
Т р е у г о л ь н
д
т
р
и
а
е
н
з
а
о
в ы с о т а
п
к
П ла н и м е т р и я
у
у г о л
т оч к а
б
и к
с
с
е
к
т
р я м а я
и
с
к а т е т
21.
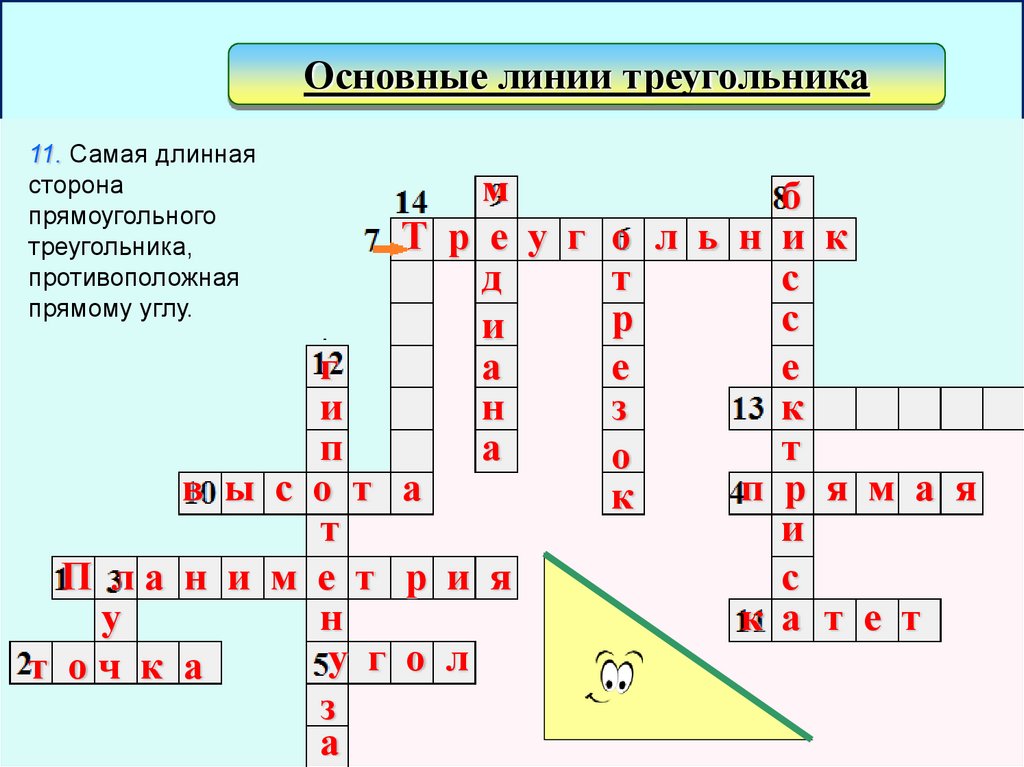
Основные линии треугольника11. Самая длинная
сторона
прямоугольного
треугольника,
противоположная
прямому углу.
м
б
Т р е у г о л ь н и к
д
т
с
р
с
и
г
а
е
е
и
н
з
к
п
а
т
о
в ы с о т а
п р я м а я
к
т
и
П ла н и м е т р и я
с
у
н
к а т е т
у г о л
т оч к а
з
а
22.
Внеший угол треугольникаВнешним углом ɑ Δ ABC при
вершине A называется угол,
смежный углу треугольника при
вершине A.
В
β
ɑ
γ
δ
А
ɑ= β + δ
ɑ>γ
•внешний угол треугольника равен сумме двух других углов,
не смежных с ним;
•внешний угол треугольника больше любого внутреннего
угла, не смежного с ним;
С
23.
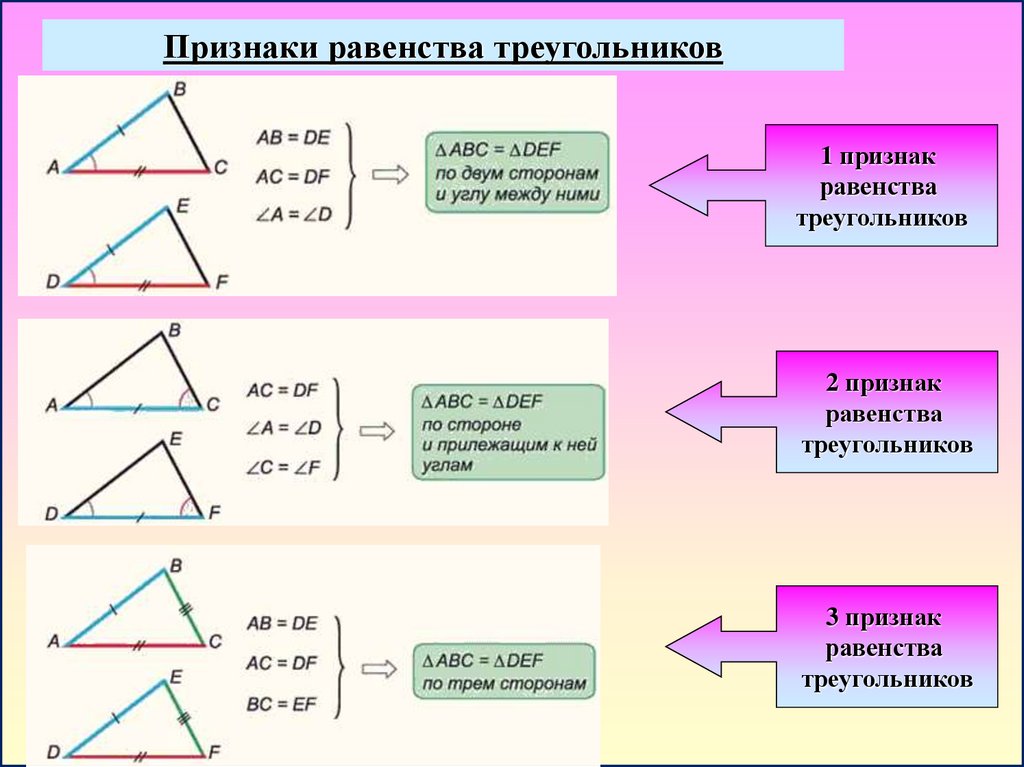
Признаки равенства треугольников1 признак
равенства
треугольников
2 признак
равенства
треугольников
3 признак
равенства
треугольников
24.
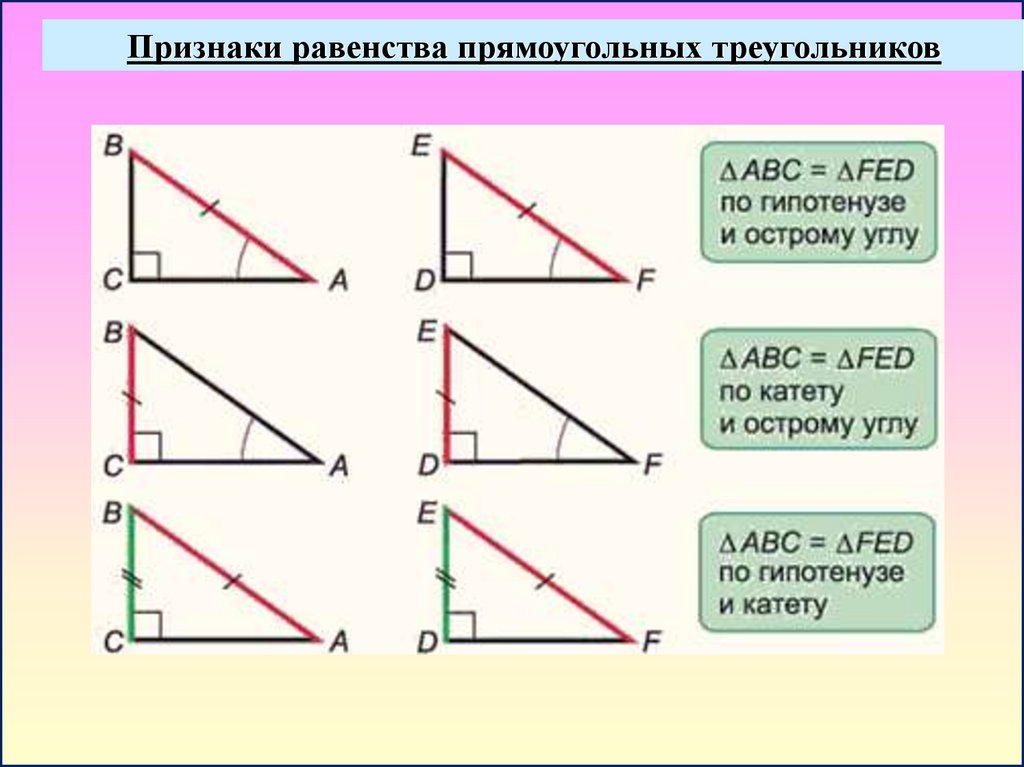
Признаки равенства прямоугольных треугольников25.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другуюПараллельные прямые
Две различные прямые либо имеют
только одну общую точку, либо не
имеют ни одной общей точки. { a ∩
а
O
b
b}=O
Две прямые на плоскости
называются параллельными, если
они не пересекаются. с //d
c
d
Через точку, не лежащую на данной
прямой, всегда можно провести прямую,
параллельную данной.
Если прямая пересекает одну из
параллельных прямых, то она пересекает и
другую.
c
d
m
26.
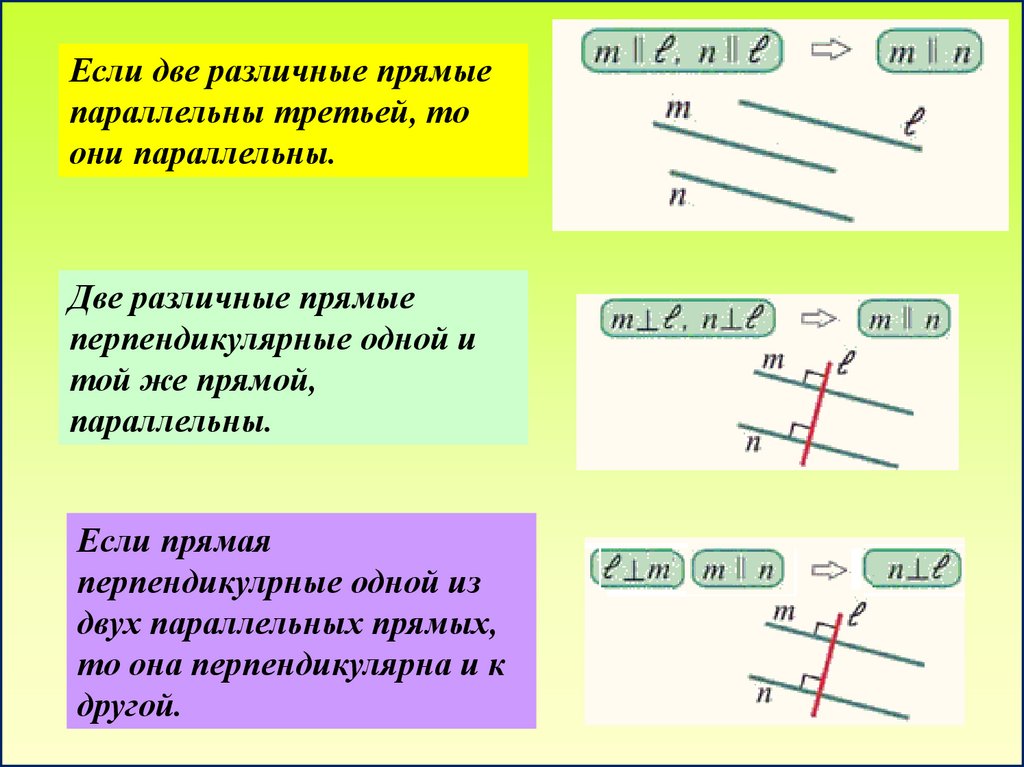
Если две различные прямыепараллельны третьей, то
они параллельны.
Две различные прямые
перпендикулярные одной и
той же прямой,
параллельны.
Если прямая
перпендикулрные одной из
двух параллельных прямых,
то она перпендикулярна и к
другой.
27.
Признаки параллельности прямыхЕсли две параллельные
прямые пепесечены секущей
то
•накрест лежащие углы равны;
•сумма односторонних углов равна 1800;
•соответственные углы равны;
28.
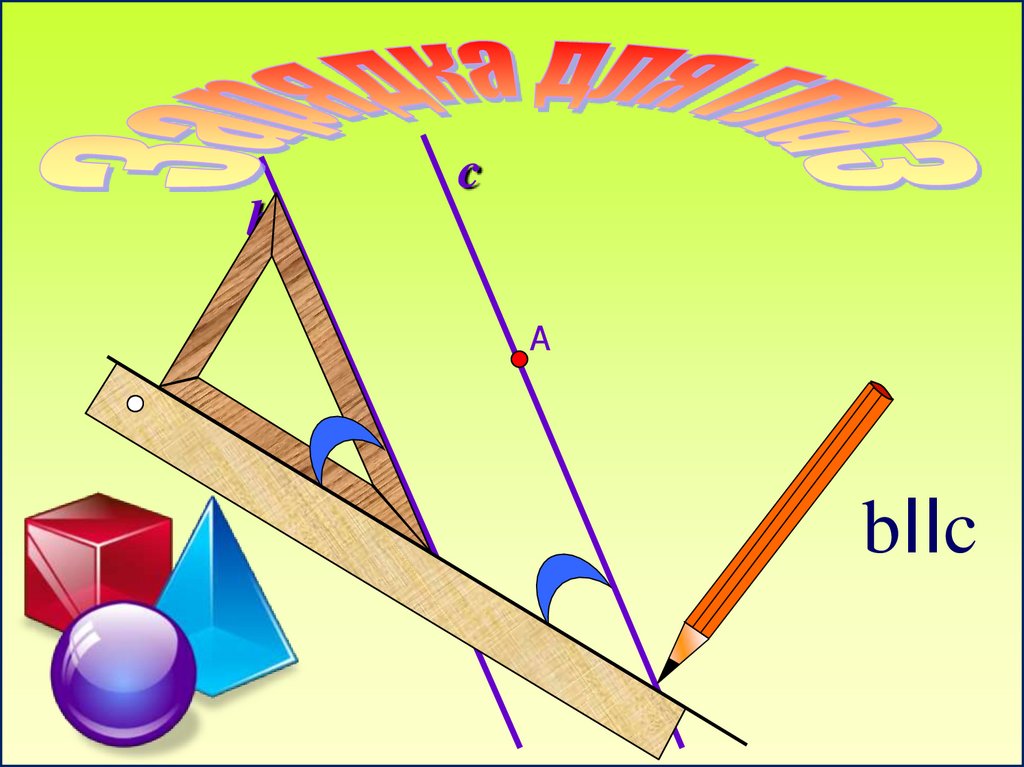
cb
А
bIIc
29.
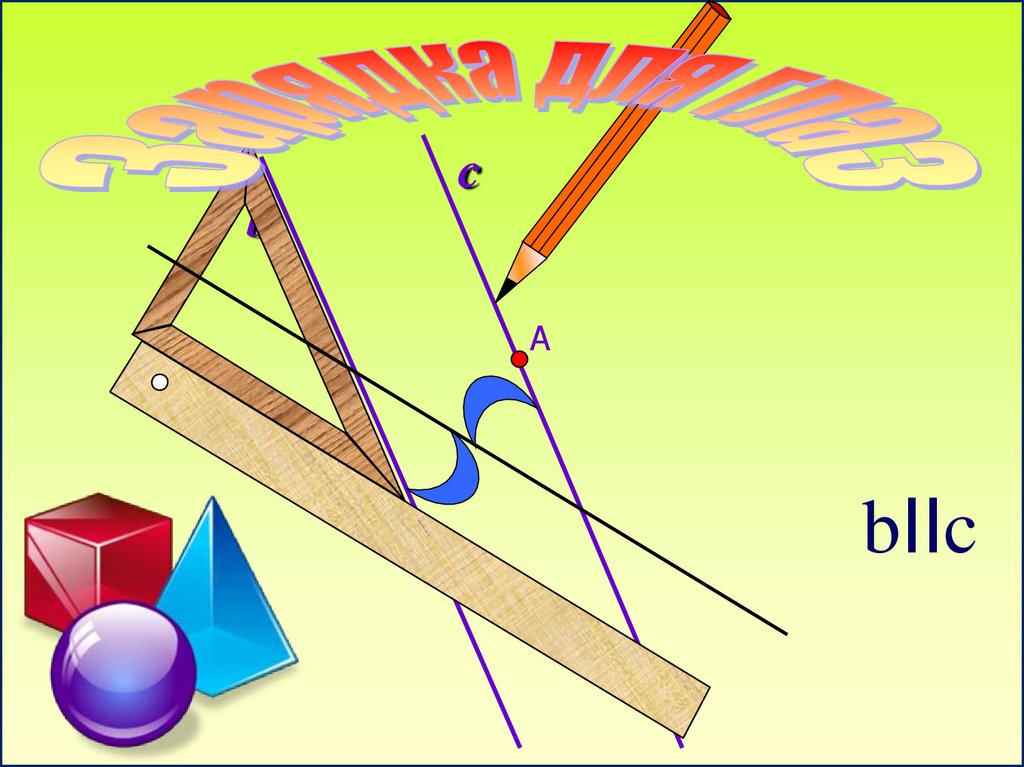
cb
А
bIIc
30.
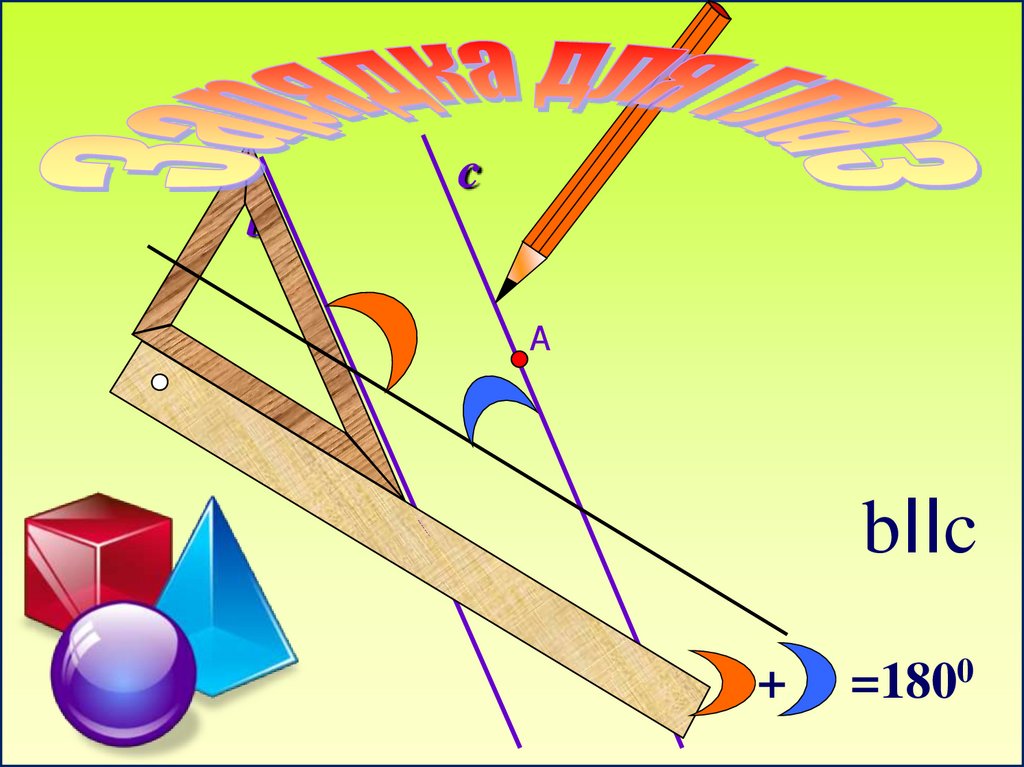
cb
А
bIIc
+
=1800
31.
a_|_ca
32.
Задача 1.Дано: 1=270; 2=1530
Доказать: m//n
1
m
3
n
2
Доказательство:
1 = 3 = 270 – т.к. вертикальные углы;
2 и 3 – соотвественные углы,
=> m//n
2+ 3= 1800
33.
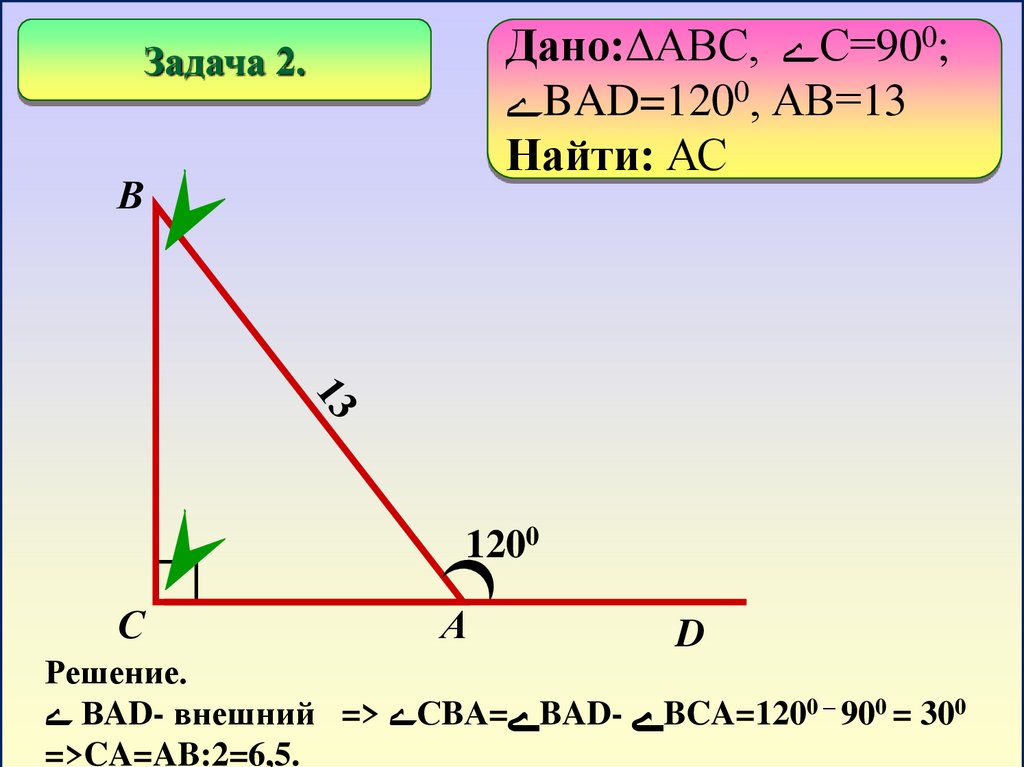
Дано:ΔАВС, С=900; BAD=1200, АВ=13
Найти: АС
Задача 2.
В
1200
С
А
D
Решение.
ВAD- внешний => СBА= BAD- BCA=1200 – 900 = 300
=>CA=AB:2=6,5.
34.
Дано: MO=ON; ; M= NДоказать:ΔMOK=ΔNOP
Задача 3.
P
М
О
N
K
Доказательство:
MOK = PON – т.к. вертикальные углы;
MO=ON;
MOK= PON;
KMO= ONP;
=> ΔMOK=ΔNOP - по II
признаку равенства Δ.
35.
Задача 4.В
Дано: BD – высота и биссектрисса
ΔАВС
Доказать:ΔАВС - равнобедренный
Доказательство:
ABD= CBD – т.к. BD- биссектриса;
ADB= CDB=900 – т.к. BD- высота
А
С
D
=> ΔABD=ΔCBD - по II
признаку равенства Δ.
AB = BC => ΔАВС - равнобедренный
36.
Я вспомнил…Я умею…
13. Утверждение,
устанавливающее
некоторое свойство и
принимаемое без
доказательства.
14. Утверждение,
требующее
доказательства
м
б
Т р е у г о л ь н и к
е
д
т
с
о
р
с
и
р а
г
е
е
и е
н
з
а к с и ом а
п м а
т
о
в ы с о т а
п р я м а я
к
т
и
П ла н и м е т р и я
с
у
н
к а т е т
у г о л
т оч к а
з
а
37.
ДЗ:знать опорный конспект,№ 297, 298
До новых
встреч
38.
Аксиома. ТеоремаДоказательство – рассуждение, устанавливающее какое-либо свойство.
Теорема – утверждение, устанавливающее некоторое свойство и требующее
доказательства. Теоремы называются также леммами, свойствами,
следствиями, правилами, признаками, утверждениями. Доказывая теорему, мы
основываемся на ранее установленных свойствах; некоторые их них также
являются теоремами. Однако некоторые свойства рассматриваются в геометрии
как основные и принимаются без доказательств.
Аксиома – утверждение, устанавливающее некоторое свойство и принимаемое
без доказательства. Аксиомы возникли из опыта, и опыт же проверяет их
истинность в совокупности. Можно построить систему аксиом различными
способами. Однако важно, чтобы принятый набор аксиом был минимальным и
достаточным для доказательства всех остальных геометрических свойств.
Заменяя в этом наборе одну аксиому другой, мы должны будем доказывать
заменённую аксиому, так как она теперь уже не аксиома, а теорема.
Начальные понятия. В геометрии ( и вообще, в математике ) существуют
понятия, которым невозможно дать сколько-нибудь осмысленное определение.
Мы их принимаем как начальные понятия. Смысл этих понятий может быть
установлен только на основании опыта.
Так, понятия точки и прямой линии являются начальными.
На основе начальных понятий можно дать определения всем остальным
понятиям.
39.
Аксиомы геометрии ЕвклидаАксиома принадлежности. Через любые две точки на
плоскости можно провести прямую и притом только одну.
Аксиома порядка. Среди любых трёх точек, лежащих на
прямой, есть не более одной точки, лежащей между двух
других.
Аксиома конгруэнтности (равенства) отрезков и углов. Если
два отрезка (угла) конгруэнтны третьему, то они
конгруэнтны между собой.
Аксиома параллельных прямых. Через любую точку, лежащую
вне прямой, можно провести другую прямую, параллельную
данной, и притом только одну.
Аксиома непрерывности (аксиома Архимеда). Для любых двух
отрезков AB и CD существует конечный набор
точек A1 , A2 ,…, An , лежащих на прямой AB, таких, что
отрезки AA1 , A1A2 ,…, An -An конгруэнтны отрезку
CD, a точка B лежит между A и An .
40.
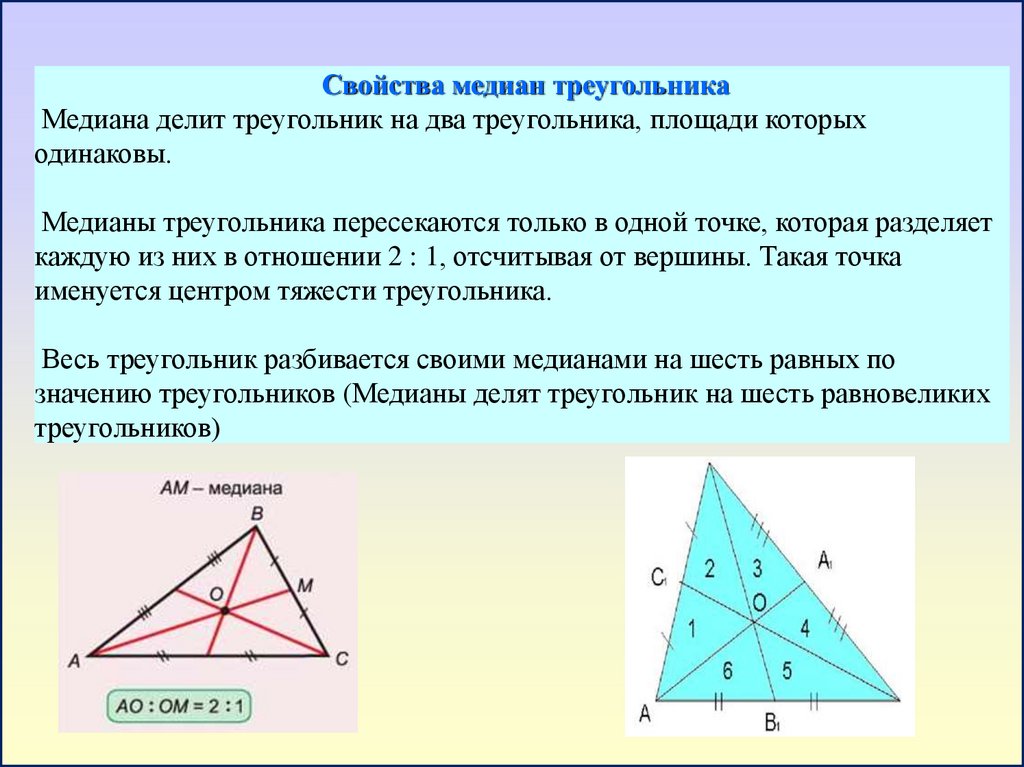
Свойства медиан треугольникаМедиана делит треугольник на два треугольника, площади которых
одинаковы.
Медианы треугольника пересекаются только в одной точке, которая разделяет
каждую из них в отношении 2 : 1, отсчитывая от вершины. Такая точка
именуется центром тяжести треугольника.
Весь треугольник разбивается своими медианами на шесть равных по
значению треугольников (Медианы делят треугольник на шесть равновеликих
треугольников)
41.
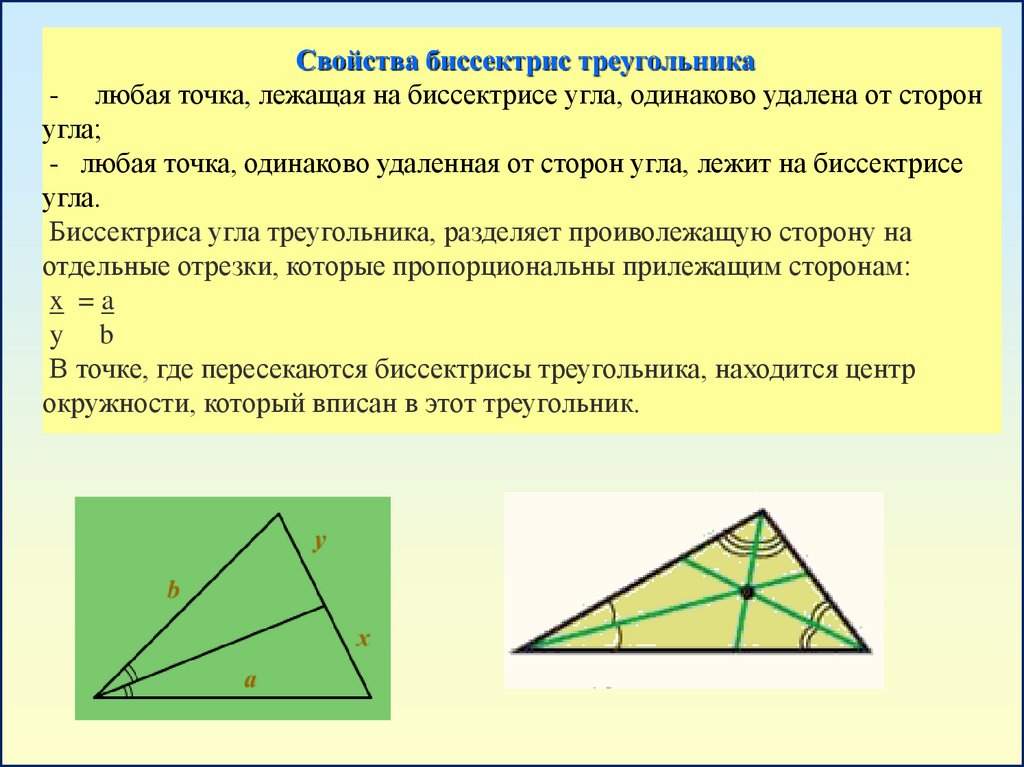
Свойства биссектрис треугольника- любая точка, лежащая на биссектрисе угла, одинаково удалена от сторон
угла;
- любая точка, одинаково удаленная от сторон угла, лежит на биссектрисе
угла.
Биссектриса угла треугольника, разделяет проиволежащую сторону на
отдельные отрезки, которые пропорциональны прилежащим сторонам:
x =a
y b
В точке, где пересекаются биссектрисы треугольника, находится центр
окружности, который вписан в этот треугольник.
42.
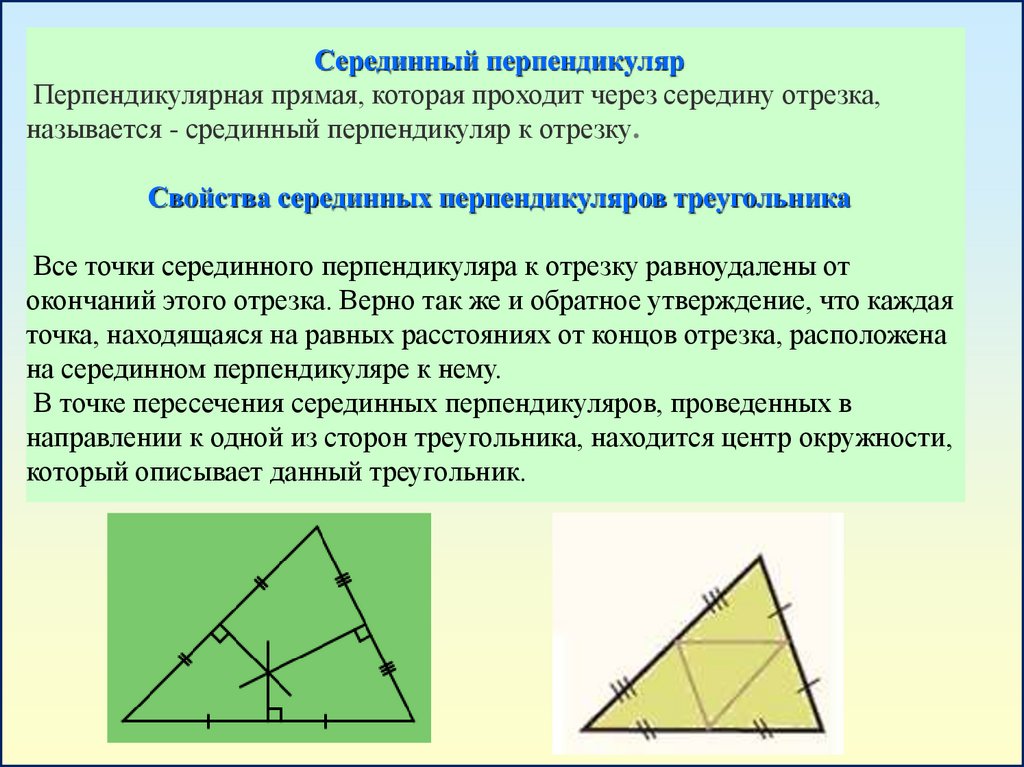
Серединный перпендикулярПерпендикулярная прямая, которая проходит через середину отрезка,
называется - срединный перпендикуляр к отрезку.
Свойства серединных перпендикуляров треугольника
Все точки серединного перпендикуляра к отрезку равноудалены от
окончаний этого отрезка. Верно так же и обратное утверждение, что каждая
точка, находящаяся на равных расстояниях от концов отрезка, расположена
на серединном перпендикуляре к нему.
В точке пересечения серединных перпендикуляров, проведенных в
направлении к одной из сторон треугольника, находится центр окружности,
который описывает данный треугольник.



















 mathematics
mathematics








