Біфуркації в нелінійних системах. Моделювання динамічних систем

1.

Лекція 10. Біфуркації в нелінійних системах.
Моделювання динамічних систем
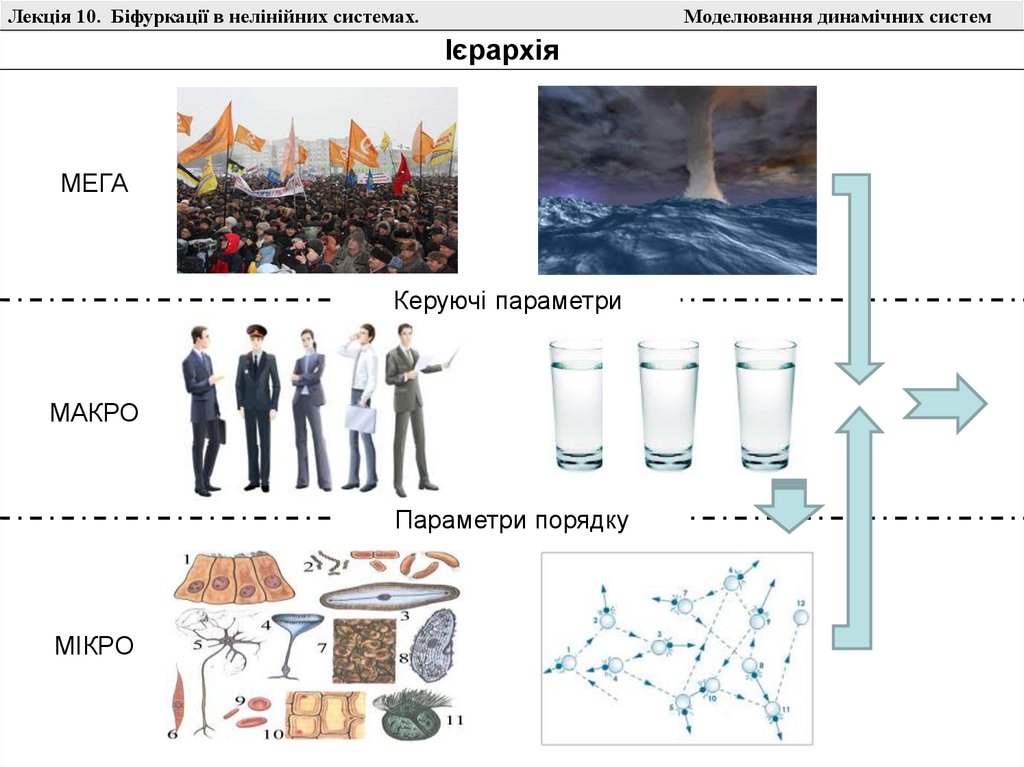
Ієрархія
МЕГА
Керуючі параметри
МАКРО
Параметри порядку
МІКРО

2.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
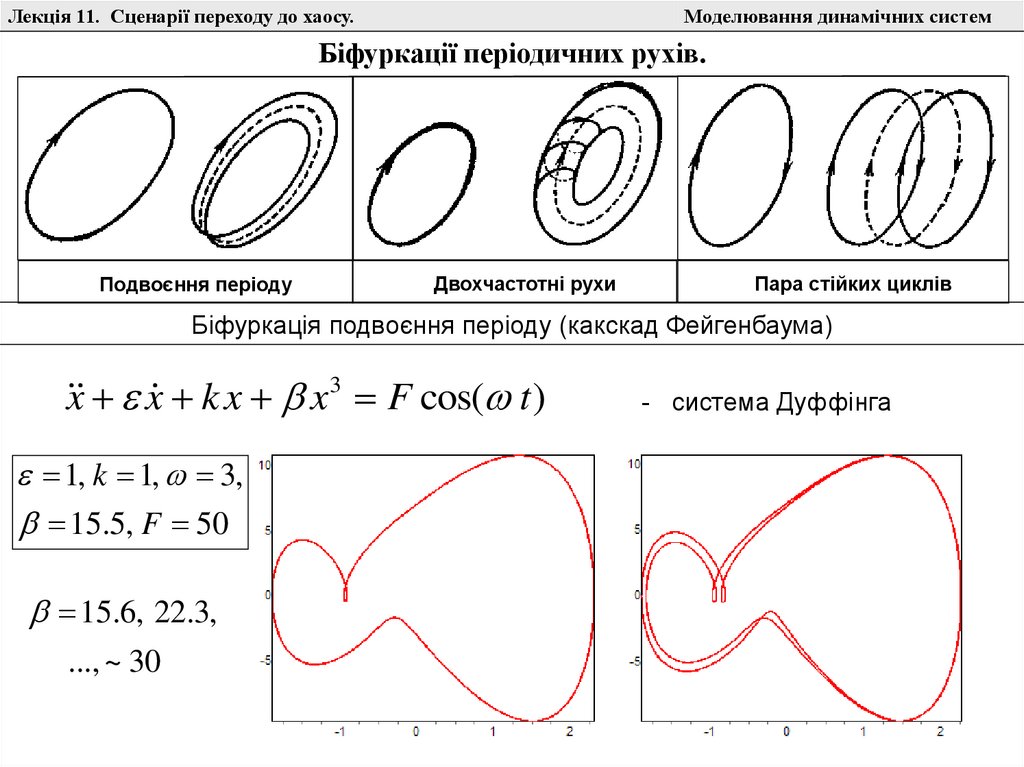
Біфуркації періодичних рухів.
Подвоєння періоду
Двохчастотні рухи
Пара стійких циклів
Біфуркація подвоєння періоду (какскад Фейгенбаума)
x x k x x 3 F cos( t )
1, k 1, 3,
15.5, F 50
15.6, 22.3,
..., ~ 30
- система Дуффінга

3.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
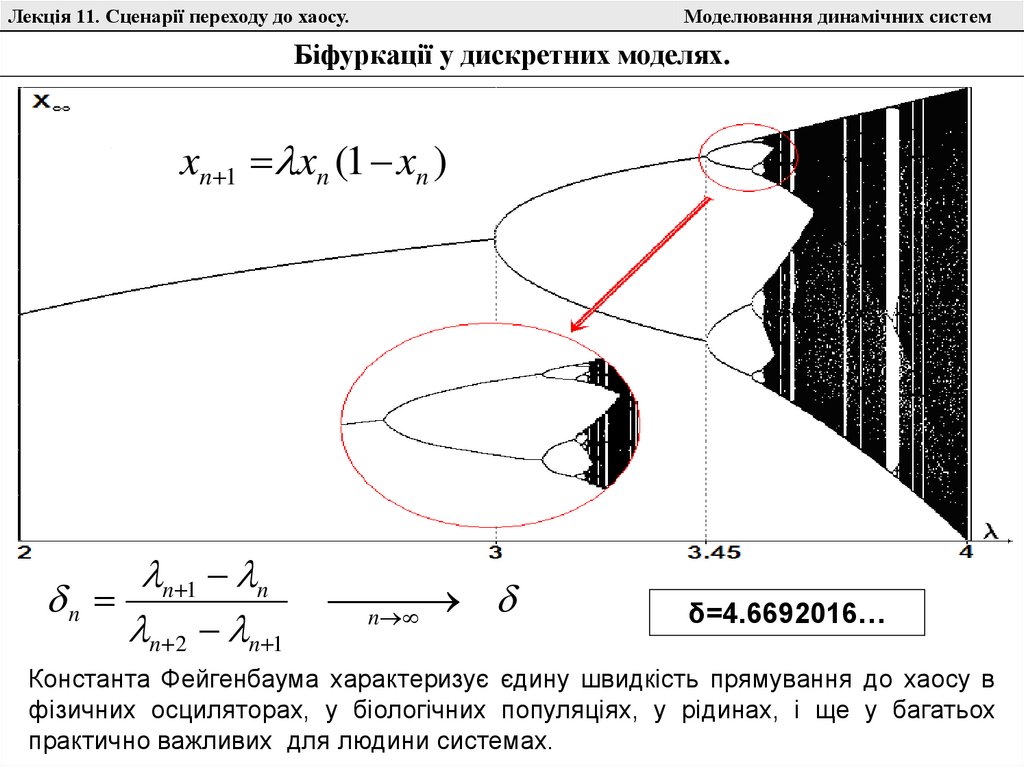
Біфуркації у дискретних моделях.
xn 1 xn (1 xn )
n 1 n
n
n 2 n 1
n
δ=4.6692016…
Константа Фейгенбаума характеризує єдину швидкість прямування до хаосу в
фізичних осциляторах, у біологічних популяціях, у рідинах, і ще у багатьох
практично важливих для людини системах.

4.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
Сценарії виходу на хаос:
ланцюжок Фейгенбаума
Рюеля - Такенса – Ньюхауза
перемежовуваність Помо - Манневілля
Сценарій Рюеля - Такенса – Ньюхауза
Розглянемо M ≥ 3 дисипативних підсистем, які виконують незалежні між
собою автоколивання (тобто на частотах, що знаходяться в ірраціональних
співвідношеннях). Атрактором такої системи буде М-мірний тор. Тепер
введемо деякий зв’язок між підсистемами, тобто незалежні рівняння їх
моделей зведемо у єдину систему (прикладом є система Лоренца). Рюель і
Такенс довели, що за будь-якого, навіть самого слабкого зв’язку між
підсистемами можна підібрати такі його вид і параметри, котрі призведуть до
появи дивного атрактора (отже й хаосу) у всій системі.
Більше того, далі Рюель і Такенс отримали ще дивовижніший результат.
Уявімо собі простір фунцій, які стоять у правих частинах динамічних рівнянь
моделі системи. Виявляється, що в довільно малому околі будь-якої точки
цього простору, що відповідає незв’язаним (регулярним) автоколиванням
підсистем існує всюди щільна множина точок, які призводять до хаотичної
динаміки.

5.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
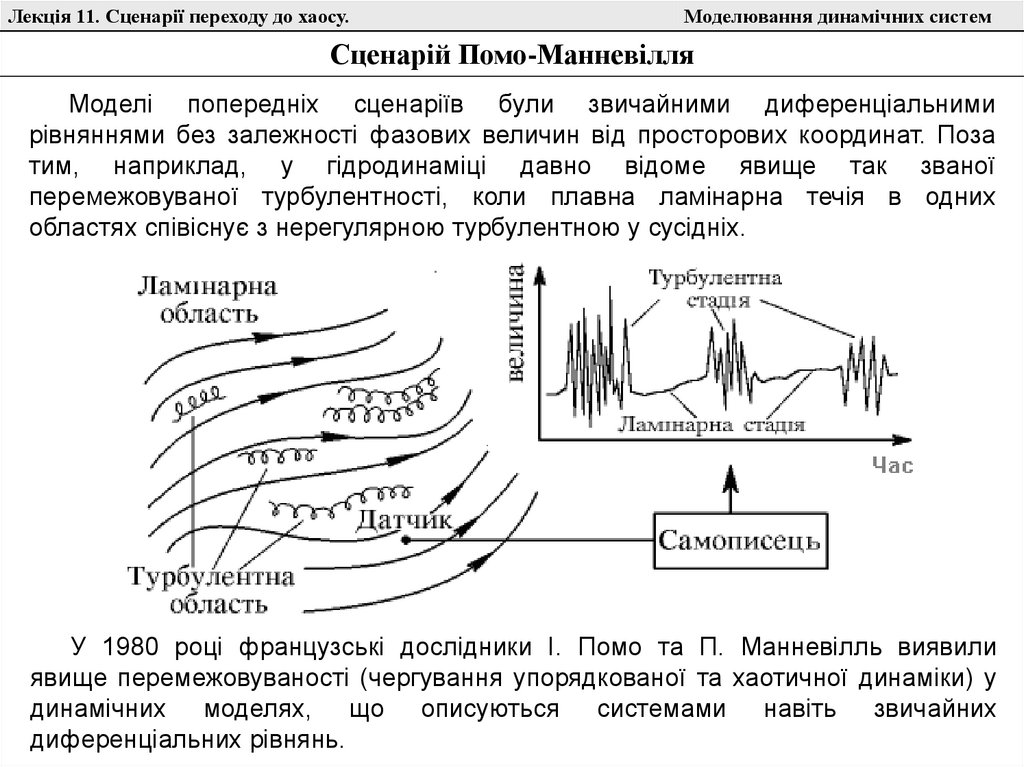
Сценарій Помо-Манневілля
Моделі попередніх сценаріїв були звичайними диференціальними
рівняннями без залежності фазових величин від просторових координат. Поза
тим, наприклад, у гідродинаміці давно відоме явище так званої
перемежовуваної турбулентності, коли плавна ламінарна течія в одних
областях співіснує з нерегулярною турбулентною у сусідніх.
У 1980 році французські дослідники І. Помо та П. Манневілль виявили
явище перемежовуваності (чергування упорядкованої та хаотичної динаміки) у
динамічних моделях, що описуються системами навіть звичайних
диференціальних рівнянь.

6.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
Ланцюжки біфуркацій. Вибір сценарію хаотизації.
Вибір визначається внутрішними властивостями системи (у моделі системи),
чи зумовлений якимись зовнішними, а, можливо, й випадковими факторами ???
Оскільки всі сценарії хаотизації починаються з переходу системи від рівноваги
до автоколивного режиму через біфуркацію Андронова-Хопфа, спостереження за
фазовим простором моделі почнемо з граничного циклу.
x f ( x, y ),
x0 f ( x0 , y0 ),
Січення Пуанкаре:
Для граничного циклу:
Вносимо збурення:
Розвиток у ряд Тейлора:
Лінійна частина збурення:
де:
y g ( x, y )
y0 g ( x0 , y0 )
x x0 ~
x,
y y0 ~
y
dx dx
F(x) A(x)x O(x 2 )
dt dt
x
x
y A y
f x ( x0 , y0 ) f y ( x0 , y0 )
A
g x ( x0 , y0 ) g y ( x0 , y0 )

7.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
Матриця Якобі, характеризує швидкість зміни початкового збурення у часі, а
її власні числа виражають це у кількісному значенні:
xs
xs
s A , s 1,2.
ys
ys
де
2
S
S
2 S A 0, 1,2
A
2
4
S f x ( x0 , y0 ) g y ( x0 , y0 )
- слід матриці Якобі, а
A f x ( x0 , y0 ) g y ( x0 , y0 ) f y ( x0 , y0 ) g x ( x0 , y0-) її визначник
Таким чином в координатах (S,A) область стійкості граничного циклу
обмежується лініями, що відповідають μ = 1, μ = -1 та A 1
S A 1 0,
S A 1 0,
A 1
A
Біфуркація Неймарка
1
Область стійкості
-2
-1
Біфуркація
подвоєння
періоду
1
-1
Біфуркація
сідловузол
2
S

8.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
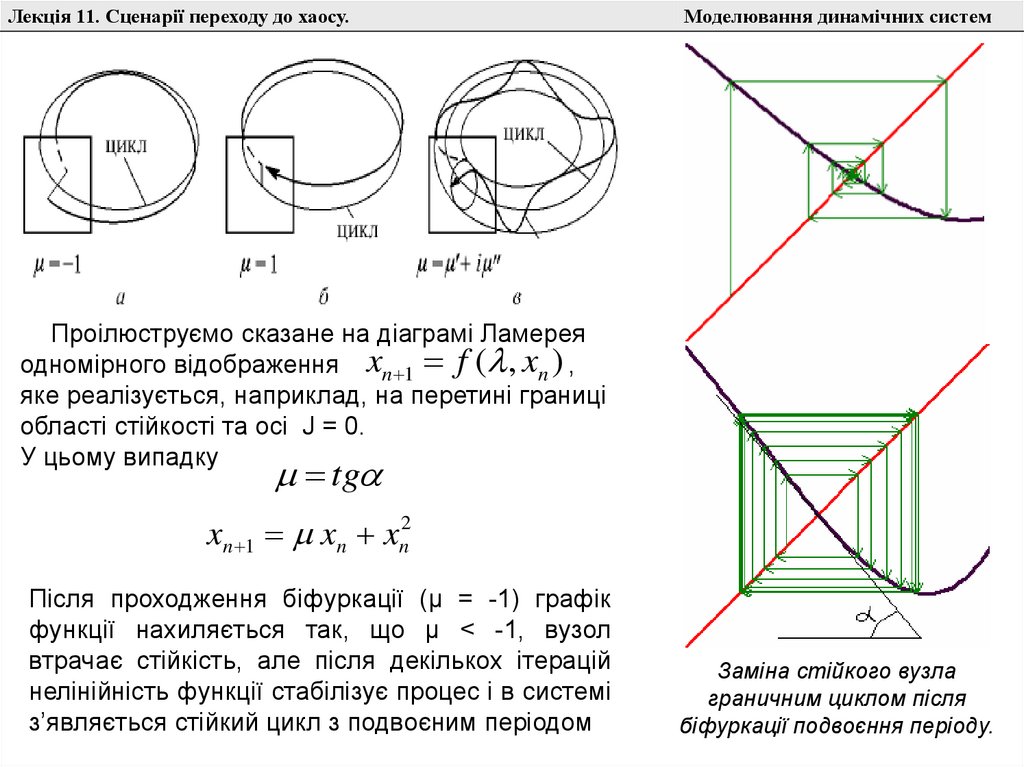
Проілюструємо сказане на діаграмі Ламерея
одномірного відображення xn 1 f ( , xn ) ,
яке реалізується, наприклад, на перетині границі
області стійкості та осі J = 0.
У цьому випадку
tg
xn 1 xn xn2
Після проходження біфуркації (μ = -1) графік
функції нахиляється так, що μ < -1, вузол
втрачає стійкість, але після декількох ітерацій
нелінійність функції стабілізує процес і в системі
з’являється стійкий цикл з подвоєним періодом
Заміна стійкого вузла
граничним циклом після
біфуркації подвоєння періоду.

9.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
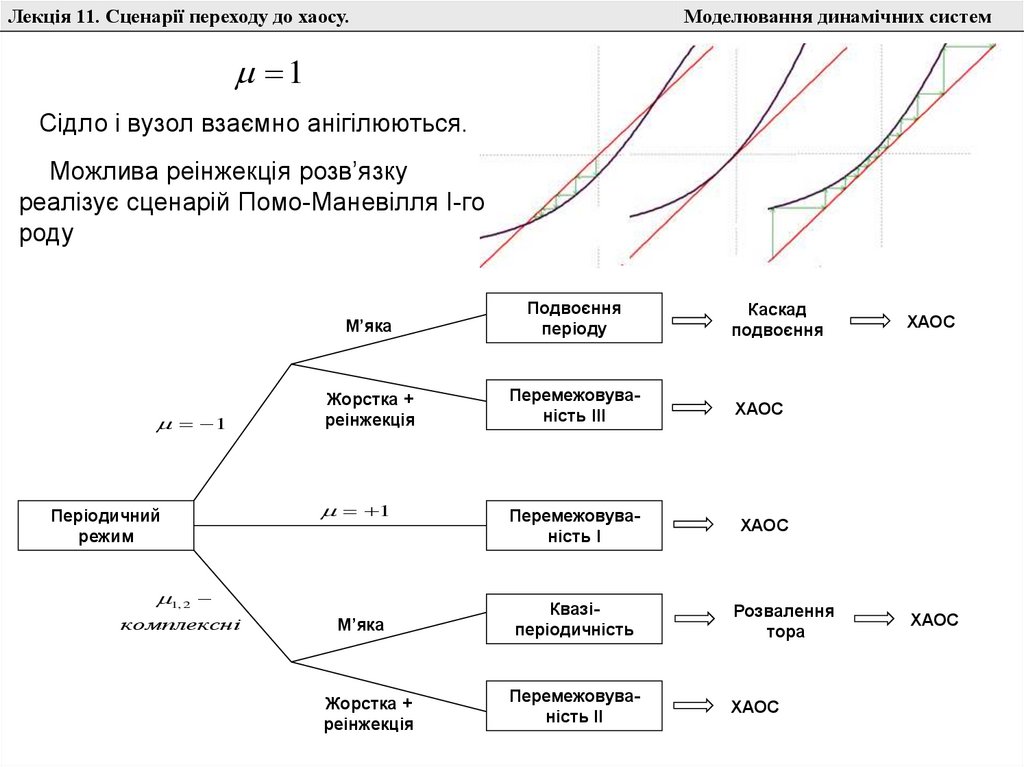
1
Сідло і вузол взаємно анігілюються.
Можлива реінжекція розв’язку
реалізує сценарій Помо-Маневілля І-го
роду
1
Періодичний
режим
М’яка
Подвоєння
періоду
Жорстка +
реінжекція
Перемежовуваність ІІІ
ХАОС
1
Перемежовуваність І
ХАОС
М’яка
Квазіперіодичність
Розвалення
тора
Жорстка +
реінжекція
Перемежовуваність ІІ
ХАОС
1, 2
комплексні
Каскад
подвоєння
ХАОС
ХАОС

10.

Лекція 11. Сценарії переходу до хаосу.
Моделювання динамічних систем
Література.
1.Кузнецов С. П. Динамический хаос (курс лекций). – М .: Изд-во физикоматематической литературы, 2001.--296 с.--ISBN 5-94052-044-8.
2.Физическая енциклопедия. http://www.femto.com.ua/articles/part_1/0327.html