Similar presentations:
Нелінійне програмування
1. НЕЛІНІЙНЕ ПРОГРАМУВАННЯ
2. План
7.1 Постановка задачі нелінійного програмування;основні труднощі в задачах нелінійного
програмування.
7.2 Графічний метод: задача з лінійною цільовою
функцією й нелінійною системою обмежень; задача
з нелінійною цільовою функцією й лінійною
системою обмежень; задача з нелінійною цільовою
функцією й нелінійною системою обмежень.
7.3 Класичний метод оптимізації: метод множників
Лагранжа.
3. 7.1 Постановка задачі нелінійного програмування. Основні труднощі в задачах нелінійного програмування
Z f ( x1 , x2 ,..., xn )g i ( x1 , x2 ,..., xn ) 0, (i 1 k ),
g i ( x1 , x2 ,..., xn ) 0, (i k 1 l ),
g ( x , x ,..., x ) 0, (i l 1 m),
n
i 1 2
7.1
7.2
4.
5.
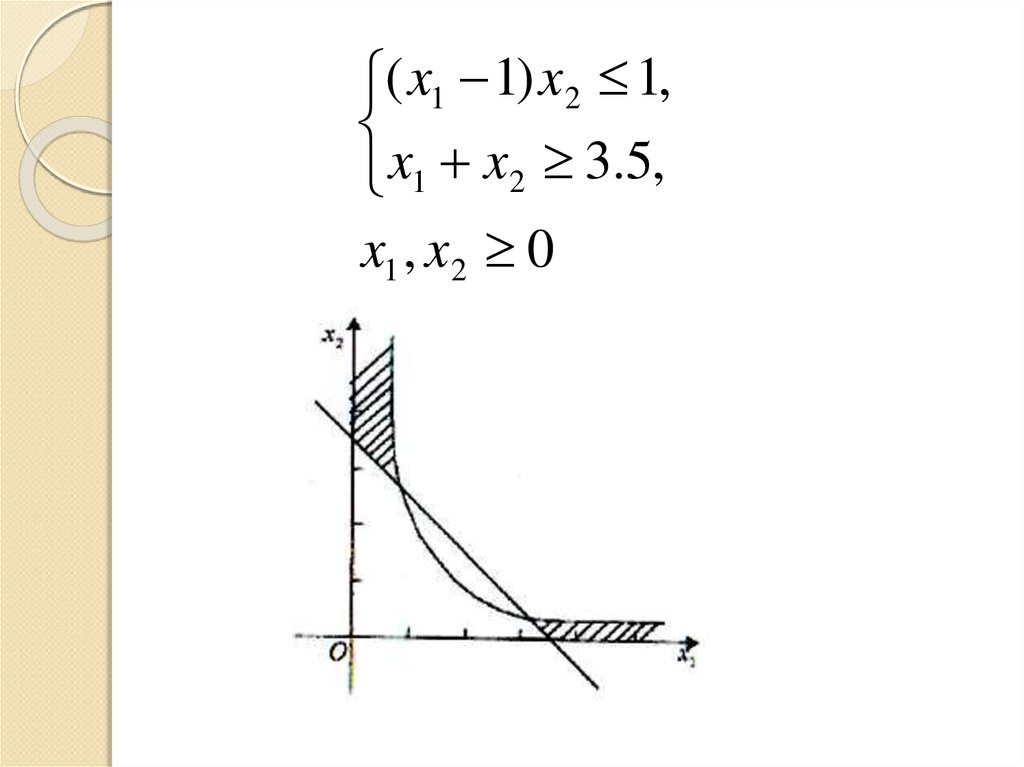
( x1 1) x2 1,x1 x2 3.5,
x1 , x2 0
6.
Сепарабельна задачаn
f ( x1 , x2 ,..., xn ) f j ( x j ) max(min)
j 1
n
a
j 1
ij
x j bi , (i 1 m)
Квадратична задача НП
n
m
n
j 1
i 1 j 1
f ( x1 , x2 ,..., xn ) c j x j d ij xi x j max(min)
n
a
j 1
ij
x j bi , (i 1 m)
Задача опуклого програмування
f ( x1 , x2 ,..., xn )
gi ( x1 , x2 ,..., xn )
7. 7.2 Графічний метод
Z f ( x1 , x2 )7.3
g i ( x1 , x2 ) bi , i 1 m,
x1 , x2 0
f ( x) c
7.4
7.5
f ( x1 , x2 ) c1 x1 c2 x2
f ( x1 , x2 ) x1 x2
2
2
r c
f ( x1 , x2 ) ( x1 a) 2 ( x2 b) 2
f ( x1 , x2 ) c( x1 a) 2 d ( x2 b) 2
8.
Приклад. Задача з лінійною цільовою функцією йнелінійною системою обмежень
z 3 x1 x2
x1 x2 2,
2
2
x
x
2 16,
1
x1 , x2 0
3x1 x2 c
2 x1 2 x2 x2' 0
k 3
x1
x
x2
'
2
9.
10.
x1x1 3 x2 ,
x 3
2
2
2
x 2 x 2 16 x1 x2 16
2
1
6
2
*
x
10 , x2
10
5
5
*
1
Z max
2
6
A 10 , 10
5
5
6
2
3 10
10 4 10
5
5
11.
x23 x2 3x1 ,
x1
x1 x2 2
x x 2
1 2
x
*
1
2 *
, x2 6
3
Z min
2
B
, 6
3
2
3
6 2 6
3
12.
Приклад. Задача з нелінійною цільовою функцією йлінійною системою обмежень
Z 5( x1 3.5) 10( x2 4)
2
x1 x2 6,
x1 2 x2 8
x x 1
1 2
x1 , x2 0
2
13.
14.
5( x1 3.5) 10( x2 4) c, c 02
2
Z max 5( 3.5) 2 10( 4) 2 221.25
x1 x2 6
5( x1 3.5) 10( x2 4) c
2
x1 3.5
1
2( x2 4)
x x 6
1 2
2
E (2.5;3.5),
Z min 5(2.5 3.5)
2
10(3.5 4) 7.5
2
15.
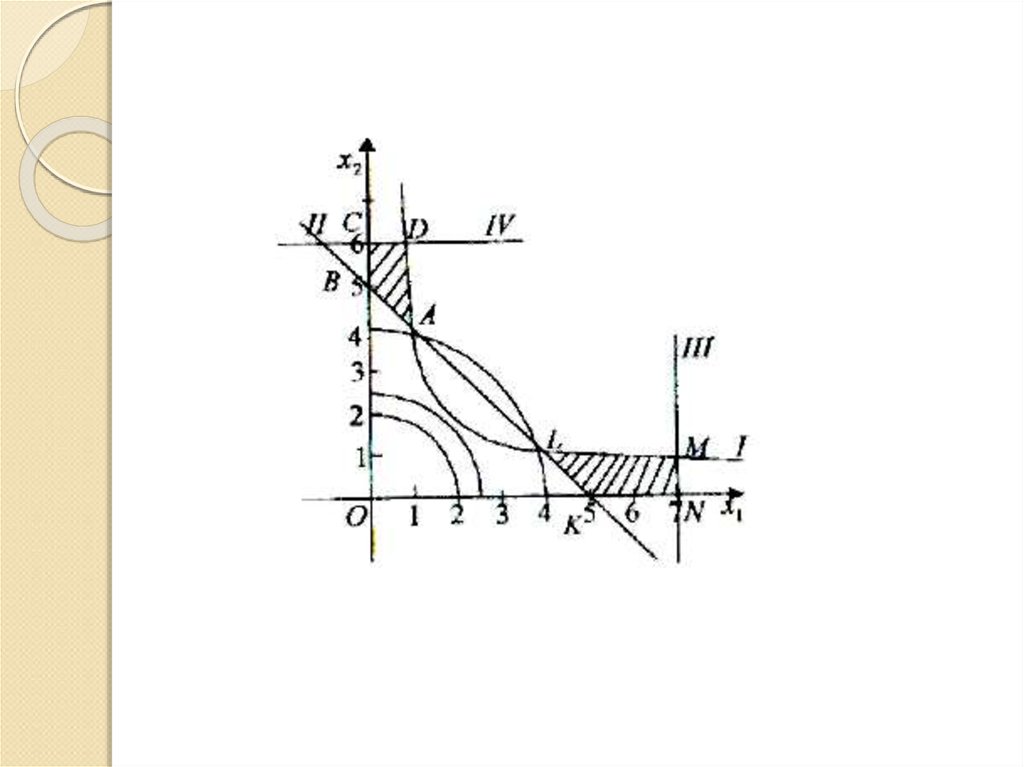
Приклад. Задача з нелінійною цільовою функцією йнелінійною системою обмежень
Z x x
2
1
2
2
x1 x2 4,
x x 5,
1 2
x
7
,
1
x2 6,
x1 , x2 0
16.
17.
x x c, c 02
1
2
2
r c
x2 6
x1 7
D:
,M :
x1 x2 4
x1 x2 4
2 4
D ;6 , M 7;
3 7
328
2417
Z ( D)
, Z (M )
9
49
Z max
2417
49
18. 7.3 Класичний метод оптимізації: метод множників Лагранжа.
x1 , x2 ,..., xnZ f ( x1 , x2 ,..., xn )
f ' ( x) 0
f ( X ) f ( X )
f ( X )
Z
;
;...;
x2
xn
x1
X ( x1 , x2 ,..., xn )
Z ( X 0 ) 0
2 f ( x1 , x2 ,..., xn )
H
, i, j 1 n
xi x j
19.
2 f ( x1 , x2 ,..., xn ) 2 f ( x1 , x2 ,..., xn )xi x j
x j xi
M 1 f11 , M 2
f11
f12
f 21
f 22
2 f (X 0 )
f ij
xi x j
X 0 ( x1 , x2 ,..., xn )
0
0
0
,..., M n
f11
f12
...
f1n
f 21
f 22
...
f 2n
...
...
...
...
f n1
f n2
...
f nn
M 1 0, M 2 0,..., M n 0,..., M n 0
M 1 0, M 2 0, , M 3 0,...
20.
ПрикладZ x x1 x2 x x1 x2 1
2
1
2
2
Z
2 x1 x2 1 0,
x1
; X 0 ( 1;1)
Z
x1 2 x2 1 0
x2
2Z (X 0 )
x1
2
2 1
2Z (X 0 )
2Z ( X 0 )
2,
1,
2, H
2
x1 x2
x2
1 2
M 1 2 0, M 2
X 0 ( 1;1)
2 1
1 2
3 0
21.
Z f ( x1 , x2 ,..., xn ) max(min)g i ( x1 , x2 ,..., xn ) bi , (i 1 m)
L( x1 , x2 ,..., xn , 1 , 2 ,..., m )
7.6
7.7
7.8
m
f ( x1 , x2 ,..., xn ) i (bi g i ( x1 , x2 ,..., xn ))
i 1
m
g i
L
f
i
0, j 1 n
x j x j i 1 x j
L
,
bi g i ( x1 , x2 ,..., xn ) 0, i 1 m
i
7.9
22.
ПрикладZ 3x 2 x
2
1
2
2
2 x1 3 x2 4,
x1 2 x2 8,
L( x1 , x2 , 1 , 2 ) 3x 2 x
2
1
2
2
1 (4 2 x1 3x2 ) 2 (8 x1 2 x2 )
L
x 6 x1 2 1 2 0,
1
L
x 4 x2 3 1 2 2 0,
2
L 4 2 x 3 x 0,
1
2
1
L 8 x 2 x 0
1
2
2
23.
2Z (X 0 )x1
2
6 0
2Z (X 0 ) 2Z ( X 0 )
6
0,
4, H
2
x1 x2
x2
0 4
M 1 6 0, M 2
6 0
0 4
24 0
X 0 ( 16;12), Z min 1056








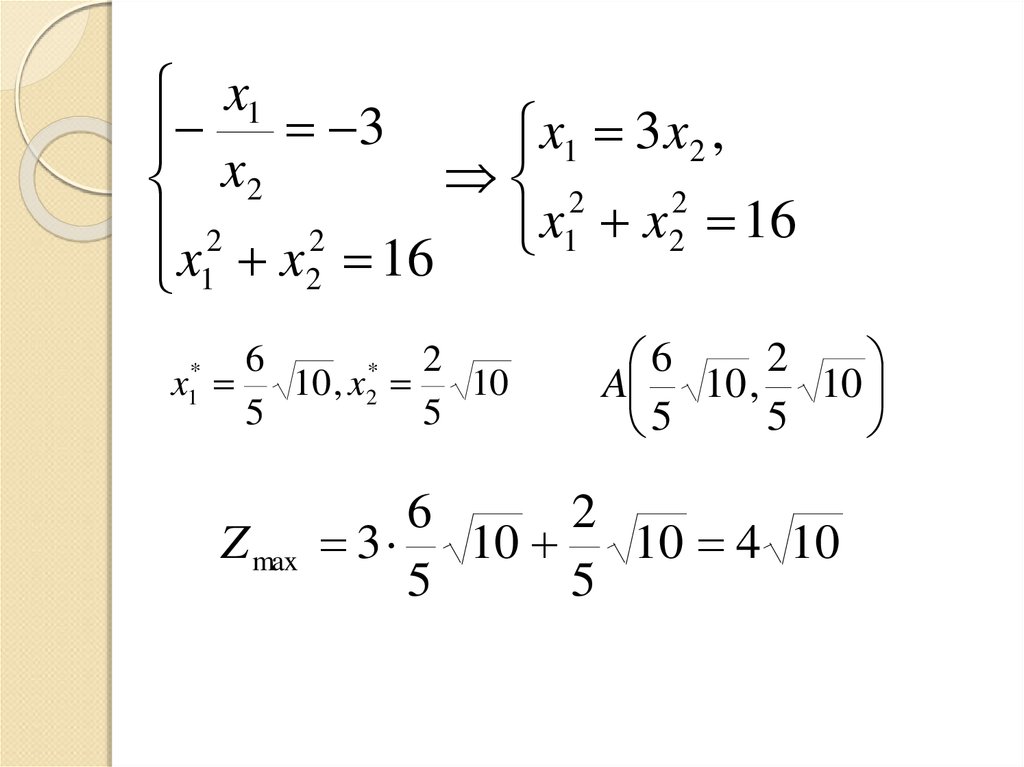
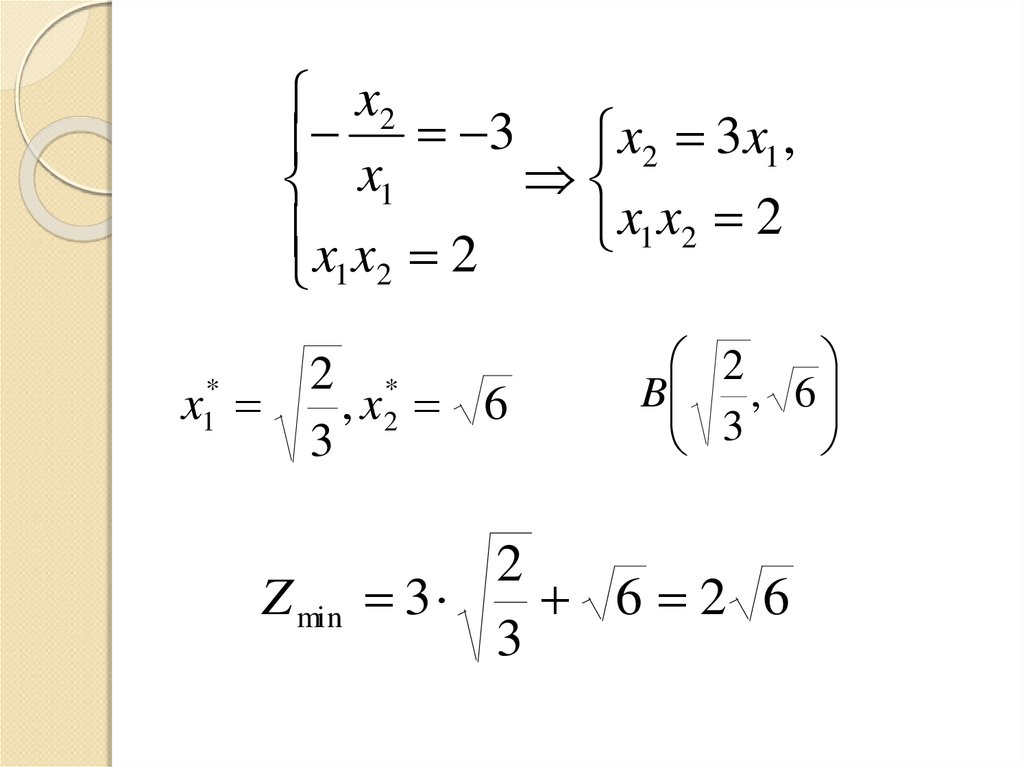


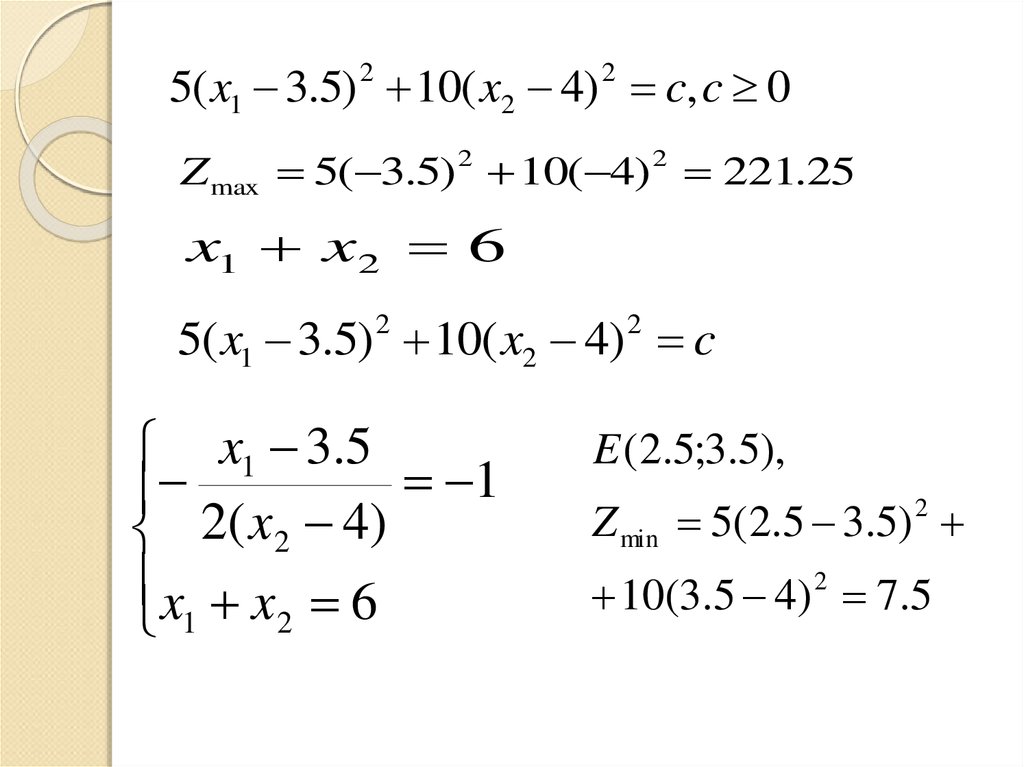



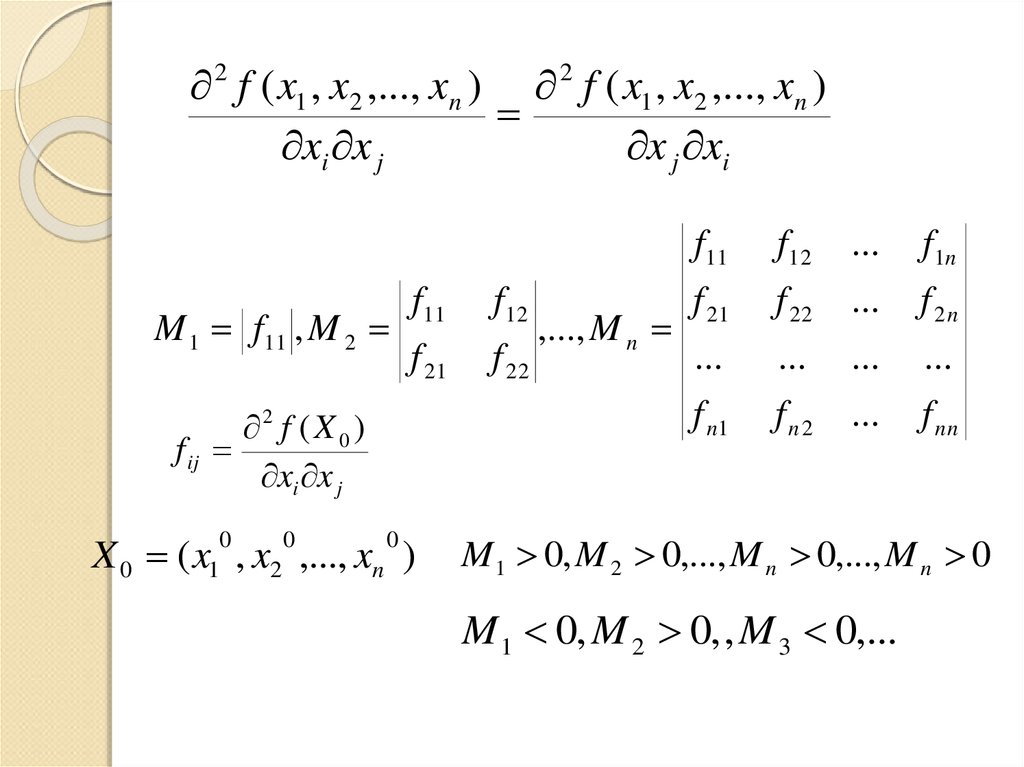

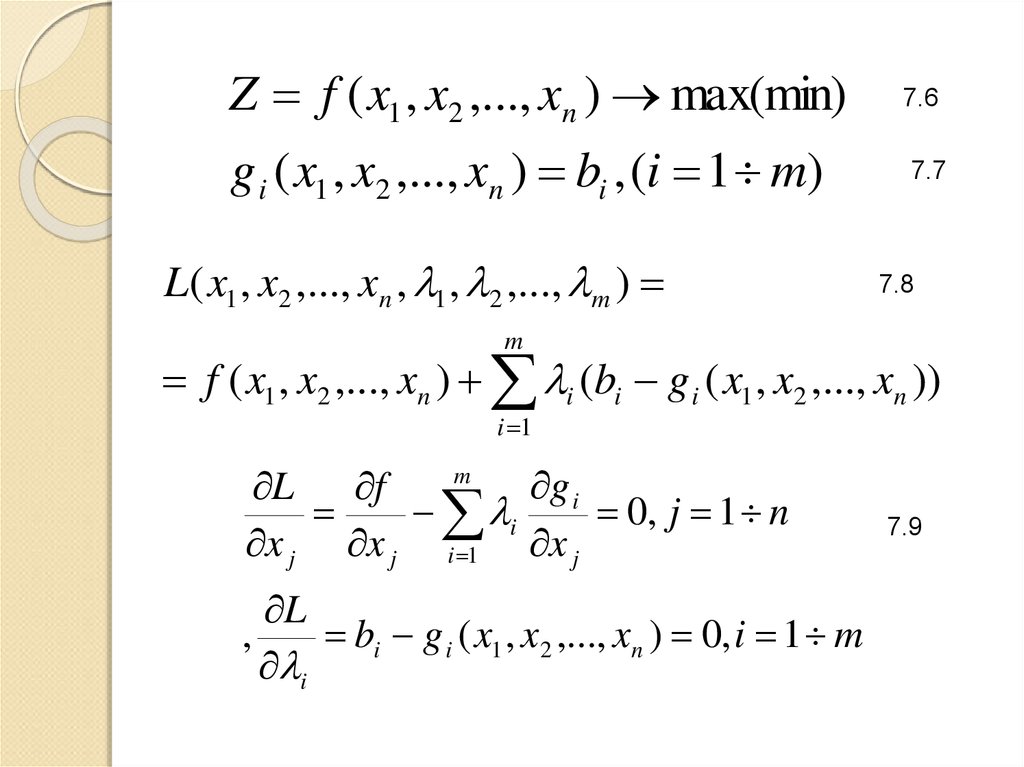


 mathematics
mathematics programming
programming








