Similar presentations:
Ряды
1.
1)Числовой ряд-это последовательность чисел.Ряд называется сходящимся, если бесконечная сумма это ряда равна конечному числу(сумма равна бесконечности-ряд
расходящийся).
Свойства:Если сходится ряд, получившийся из заданного ряда отбрасыванием нескольких его членов, то сходится и сам
заданный ряд. Если у сходящегося ряда отбросить несколько членов, то получится также сходящийся ряд.
2.
2)Оба ряда сходятся или расходятся
одновременно
3.
3)Знакопеременный ряд-это ряд,в котором присутствуют как положительные члены, так и отрицательные.Знакочередующийся ряд-это ряд типа:1-1+1-1+1-1
Достаточный признак сходимости
Если ряд
абсолютно сходится, то любой ряд, составленный из членов данного ряда, взятых,
возможно, в другом порядке, тоже абсолютно сходится и имеет ту же сумму.
Если ряды
и
абсолютно сходятся, то ряд, составленный из всевозможных попарных
произведенийumvnчленов этих рядов, тоже абсолютно сходится, и его сумма равна произведению
сумм исходных рядов.
4.
4)Функциональный ряд-это тот же числ.ряд, но вместо чисел-функция.Совокупность тех значений х, при которых функциональный ряд сходится, называется областью его
сходимости.
Функциональный рядназывается равномерно
сходящимся в некотором интервале, если он
сходится для всех x из этого интервала и если
для всякого числа
> 0 существует такое
число N > 0, зависящее от и не зависящее
от x. (при n> N выполняется неравенство
для всех x из рассматриваемого интервала).
5.
5)Степенной ряд-это ряд типа:Сходимость степенных рядов:
Если в пределе получается ноль, то алгоритм решения заканчивает свою работу, и мы даём окончательный
ответ задания: «Область сходимости степенного ряда:
»
Если в пределе получается бесконечность, то алгоритм решения также заканчивает свою работу, и мы даём
окончательный ответ задания: «Ряд сходится при
» (или при
либо
»).
Если предел равен числу, то необходимо найти область сходимости.
6.
6)Ряд МаклоренаРяд Тейлора
7.
7)Приложение степенных рядовЧтобы найти приближенное зн.функции,нужно разложить это функцию в ряд и подставить вместо х нужное значение
например:
Чтобы найти приближенное значение определенного интеграла нужно разложить подинт. Функцию в ряд и вычислить
интеграл например:
Чтобы найти приближенное решение диф.уравнений нужно разложить это уравнение в ряд например:





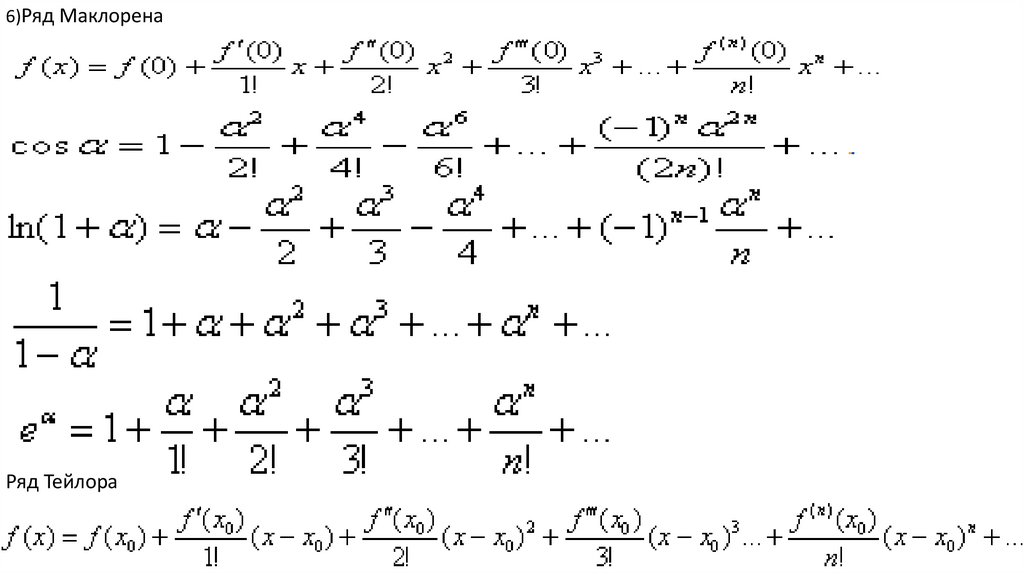



 mathematics
mathematics








