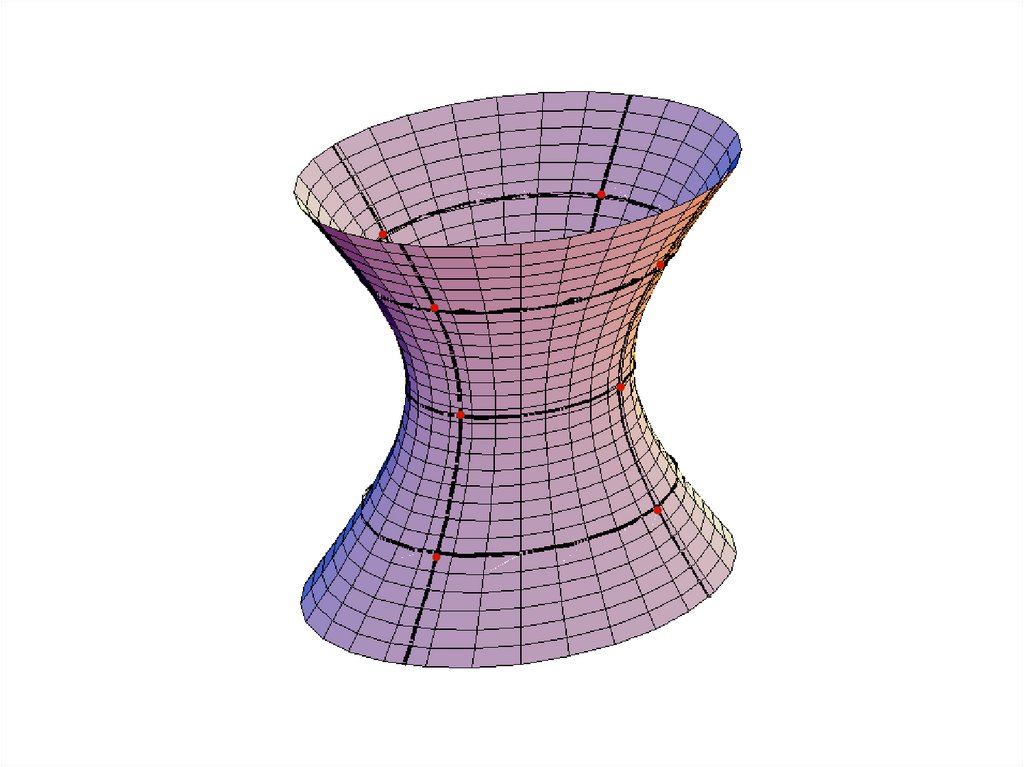
Однополостный гиперболоид

1.

Однополостный гиперболоид
Однополостным гиперболоидом называется
поверхность, каноническое уравнение которой имеет вид
2
2
2
x
y
z
2 2 1
2
a
b
c
где a, b, c – положительные числа.
Так же, как эллипсоид, он имеет три плоскости
симметрии, три оси симметрии и центр симметрии. Ими
являются соответственно координатные плоскости,
координатные оси и начало координат.

2.

z
3
-3
-2
О
2
y
3
x
x2
y2
z2
9
4
9
-3
1
a
3; b
2; c
3

3.

Сечение плоскостью XOY :
z
z
x2
y2
9
4
3
-3
-2
О
x
x2
y2
z2
9
4
9
-3
1
2
y
3
0
1

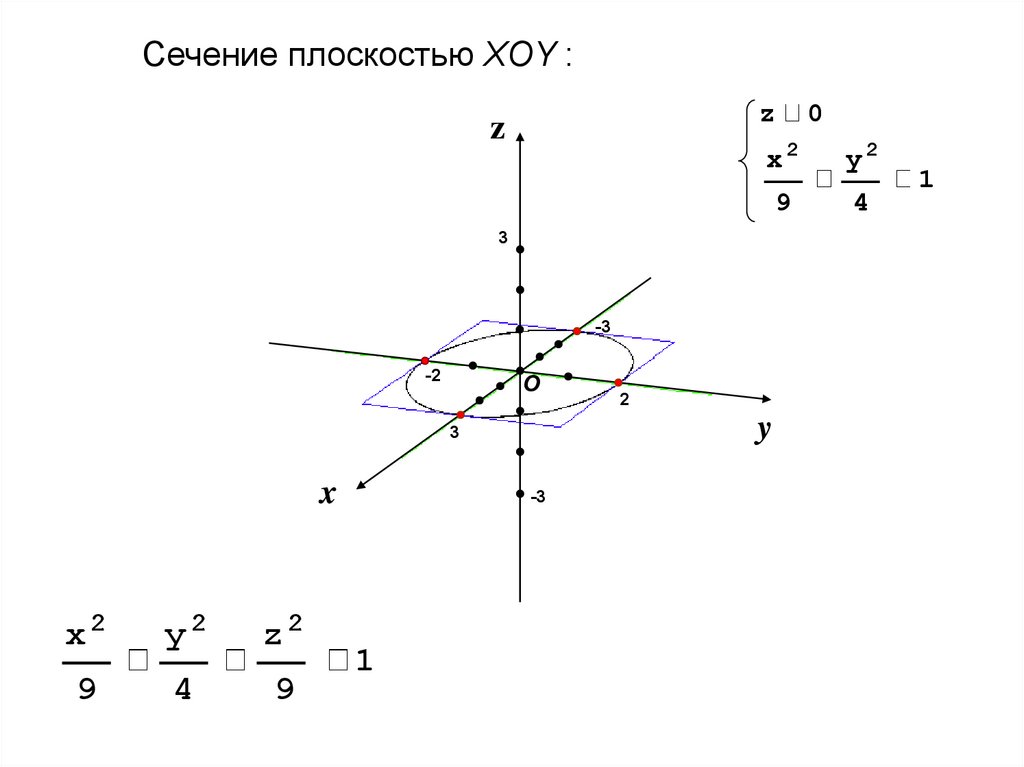
4.

Сечение плоскостью XOY :
z
z
x2
y2
9
4
3
-3
-2
О
x
x2
y2
z2
9
4
9
-3
1
2
y
3
0
1

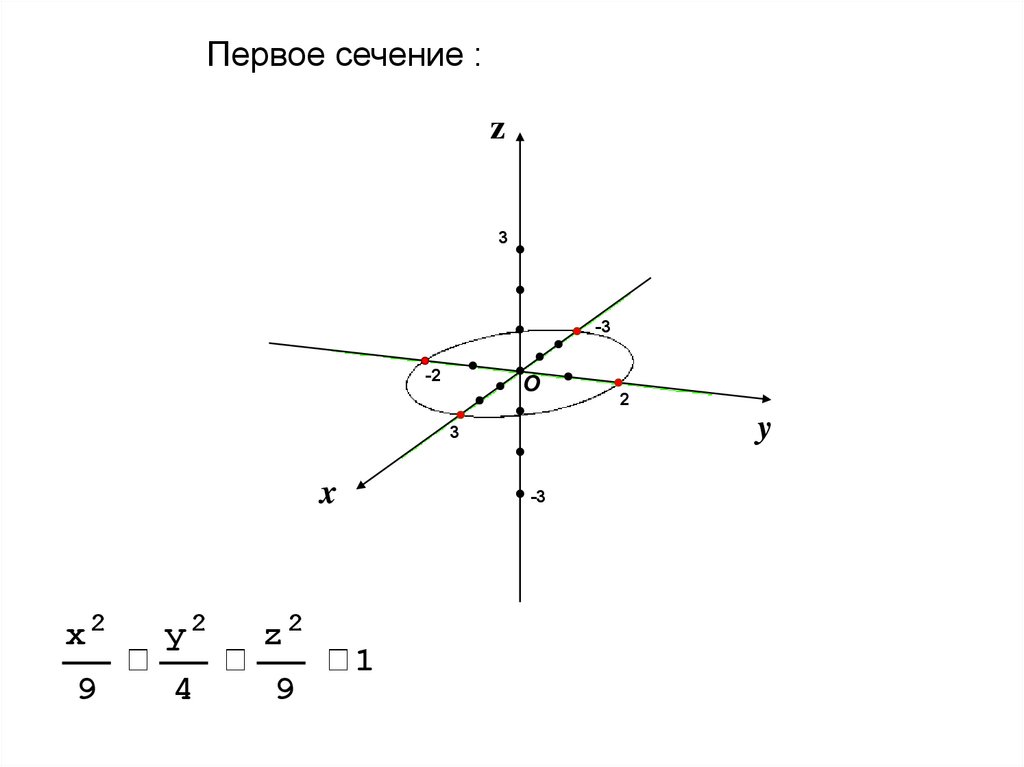
5.

Первое сечение :
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2

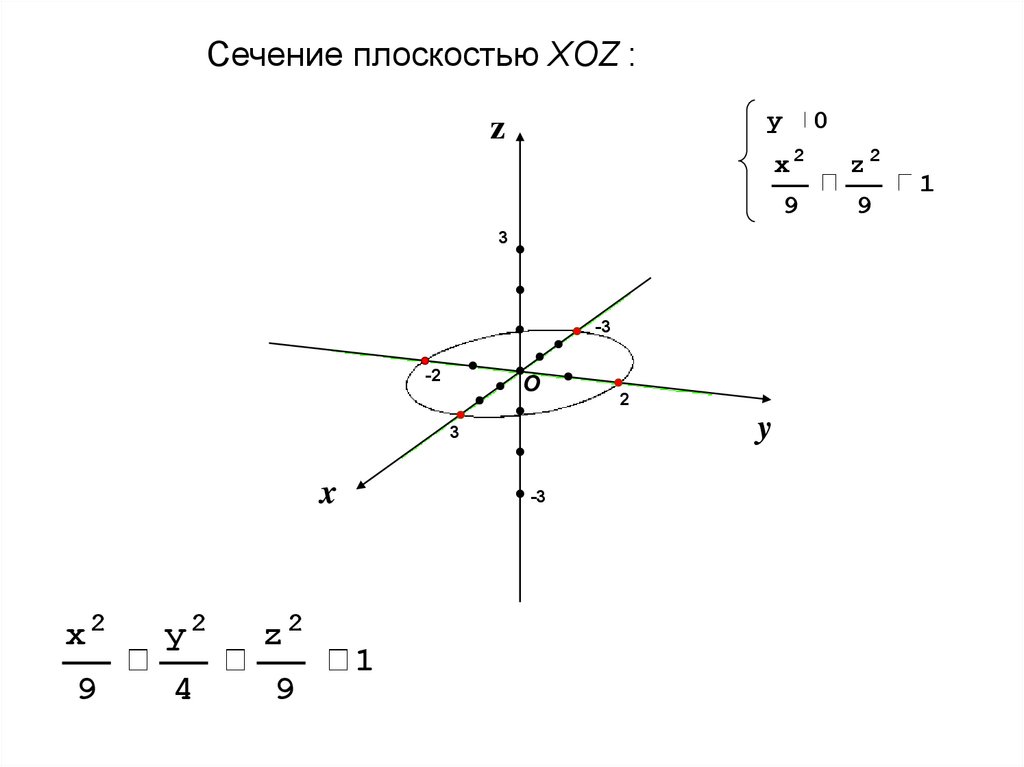
6.

Сечение плоскостью XOZ :
y
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
0
x2
z2
9
9
1

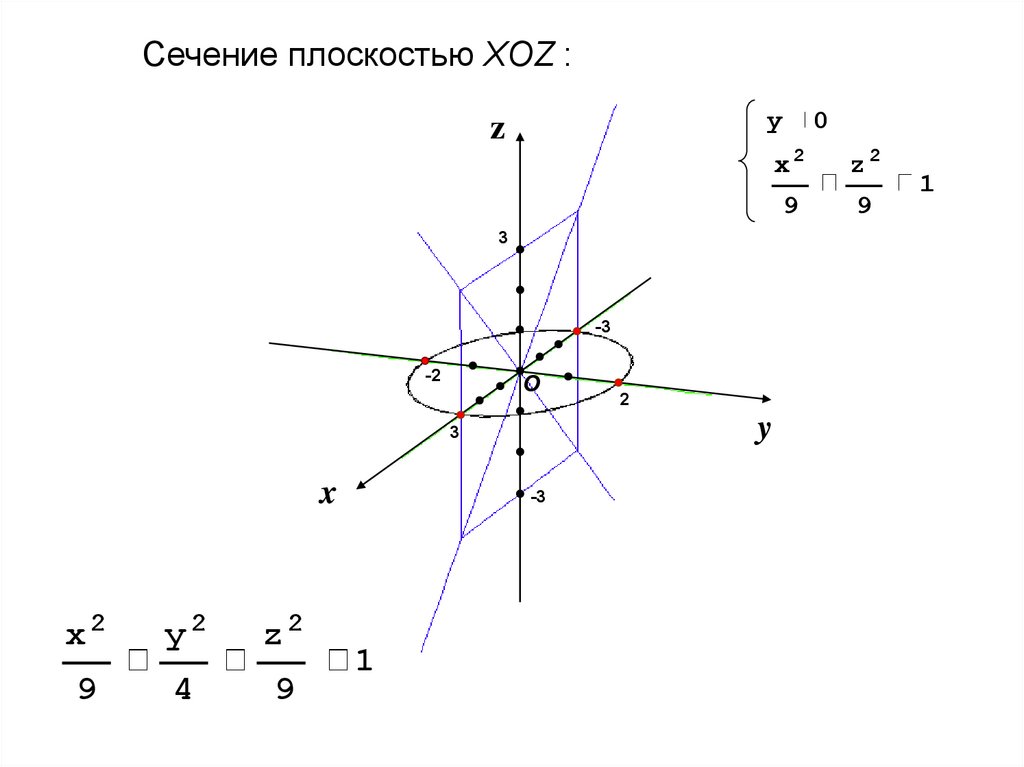
7.

Сечение плоскостью XOZ :
y
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
0
x2
z2
9
9
1

8.

Сечение плоскостью XOZ :
y
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
0
x2
z2
9
9
1

9.

Два сечения :
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2

10.

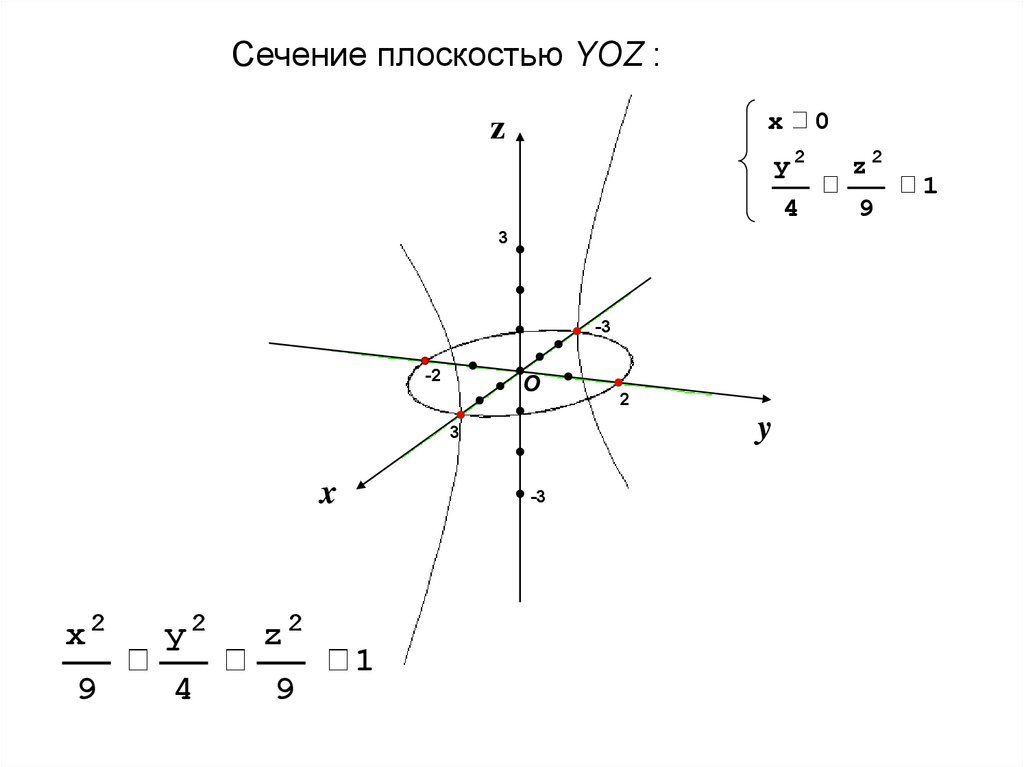
Сечение плоскостью YOZ :
x
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
0
y2
z2
4
9
1

11.

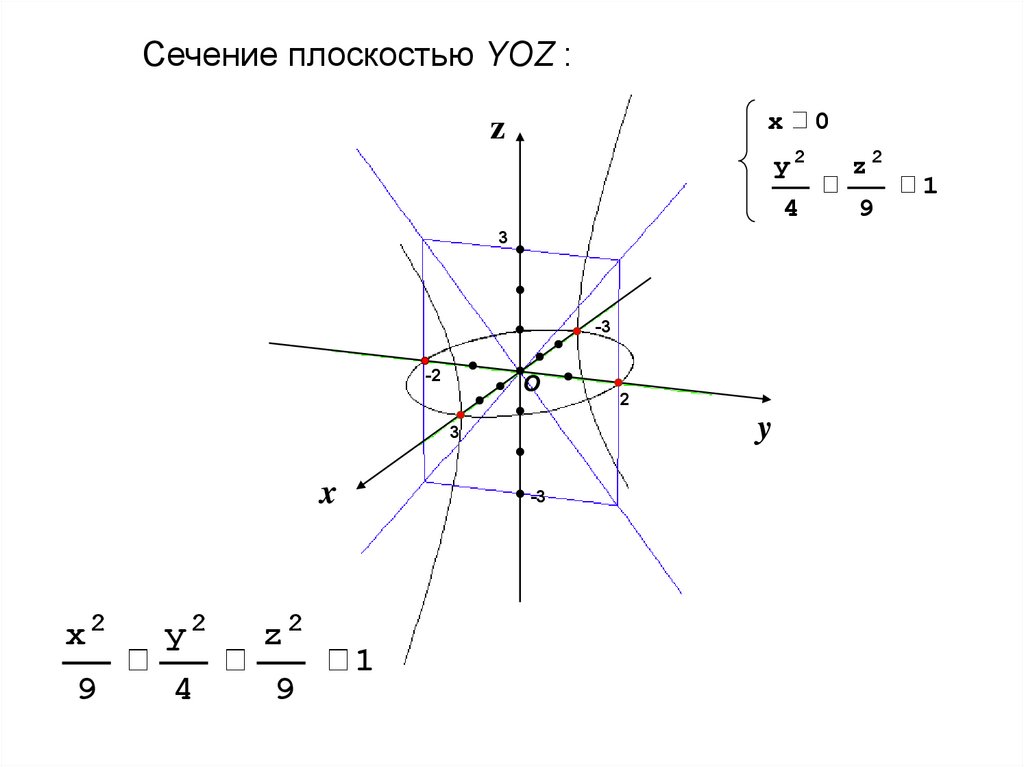
Сечение плоскостью YOZ :
x
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
0
y2
z2
4
9
1

12.

Сечение плоскостью YOZ :
x
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
0
y2
z2
4
9
1

13.

Три сечения :
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2

14.

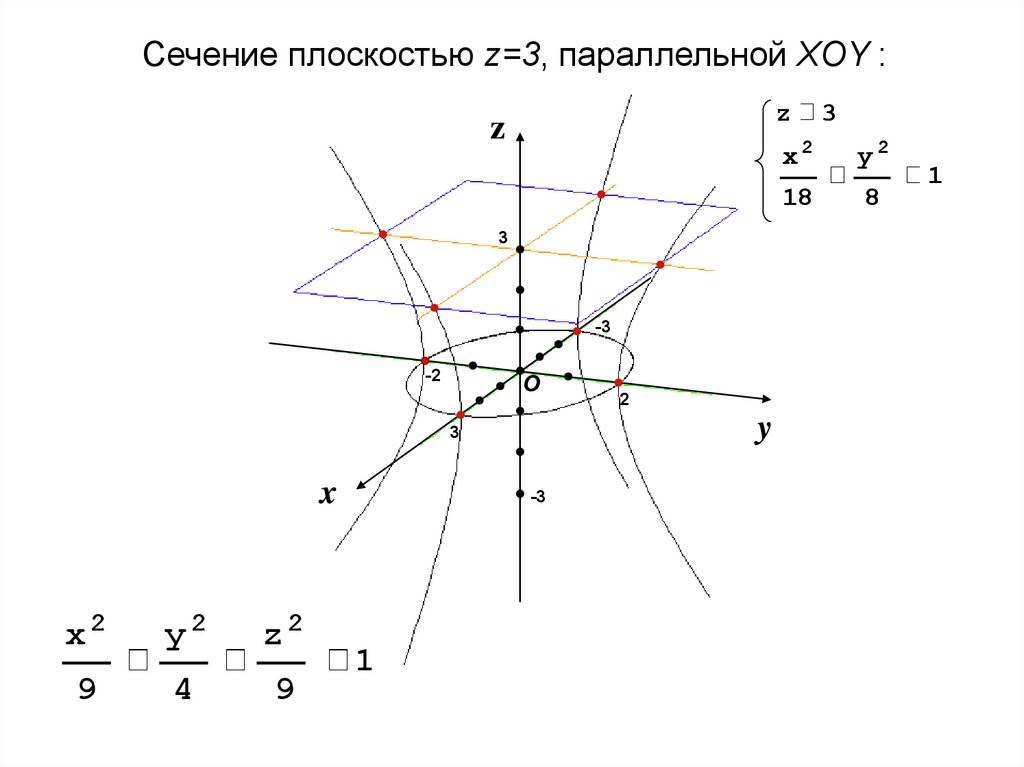
Сечение плоскостью z=3, параллельной XOY :
z
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
3
x2
y2
18
8
1

15.

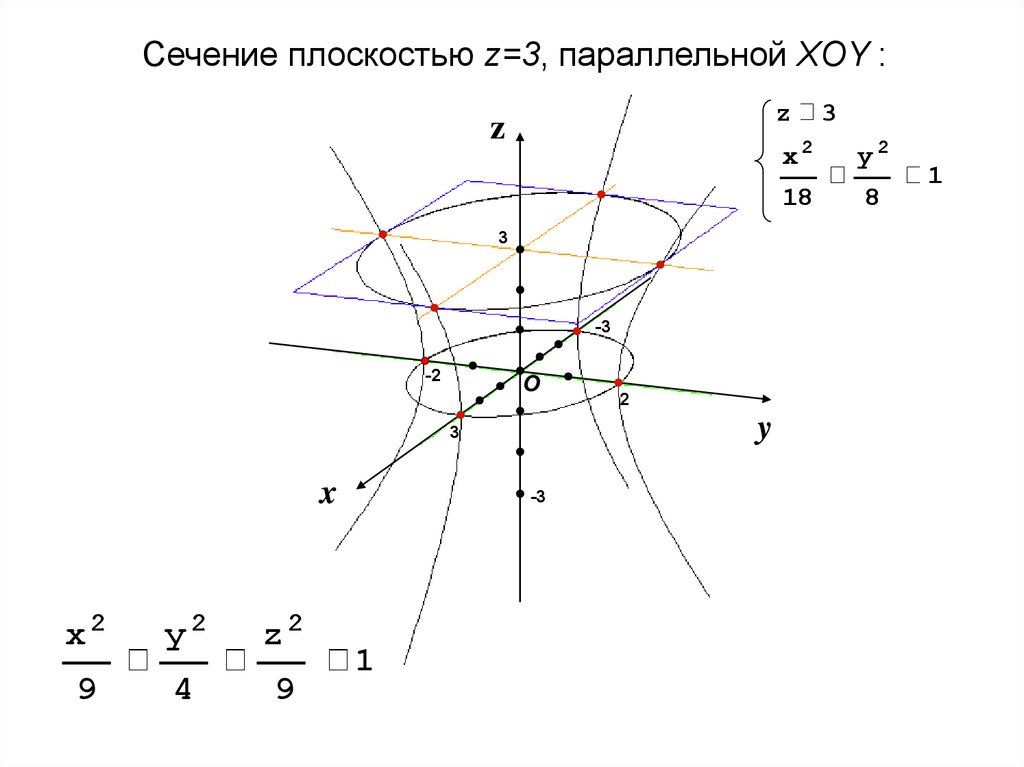
Сечение плоскостью z=3, параллельной XOY :
z
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
3
x2
y2
18
8
1

16.

Сечение плоскостью z=3, параллельной XOY :
z
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
3
x2
y2
18
8
1

17.

Четыре сечения :
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2

18.

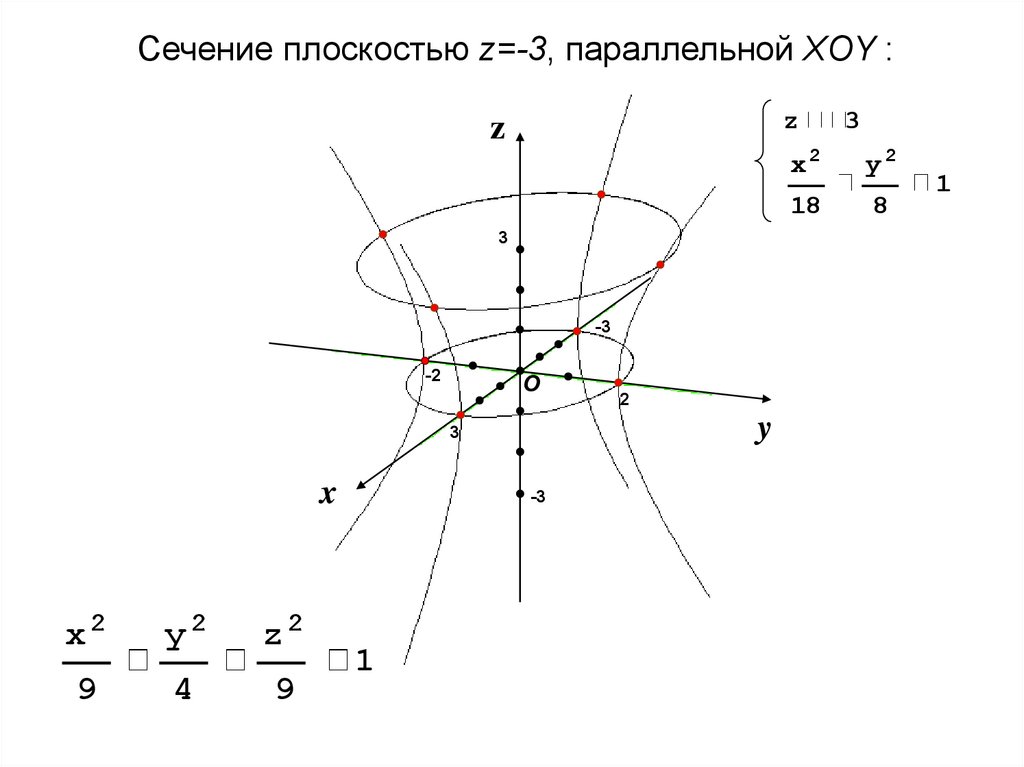
Сечение плоскостью z=-3, параллельной XOY :
z
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
3
x2
y2
18
8
1

19.

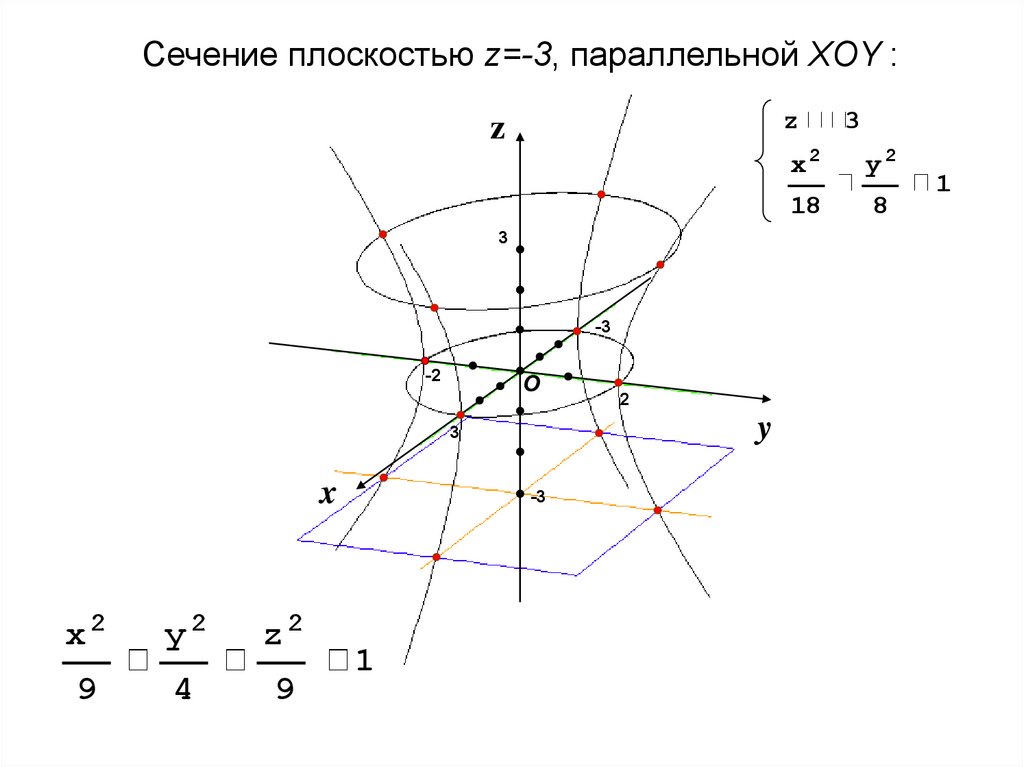
Сечение плоскостью z=-3, параллельной XOY :
z
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
3
x2
y2
18
8
1

20.

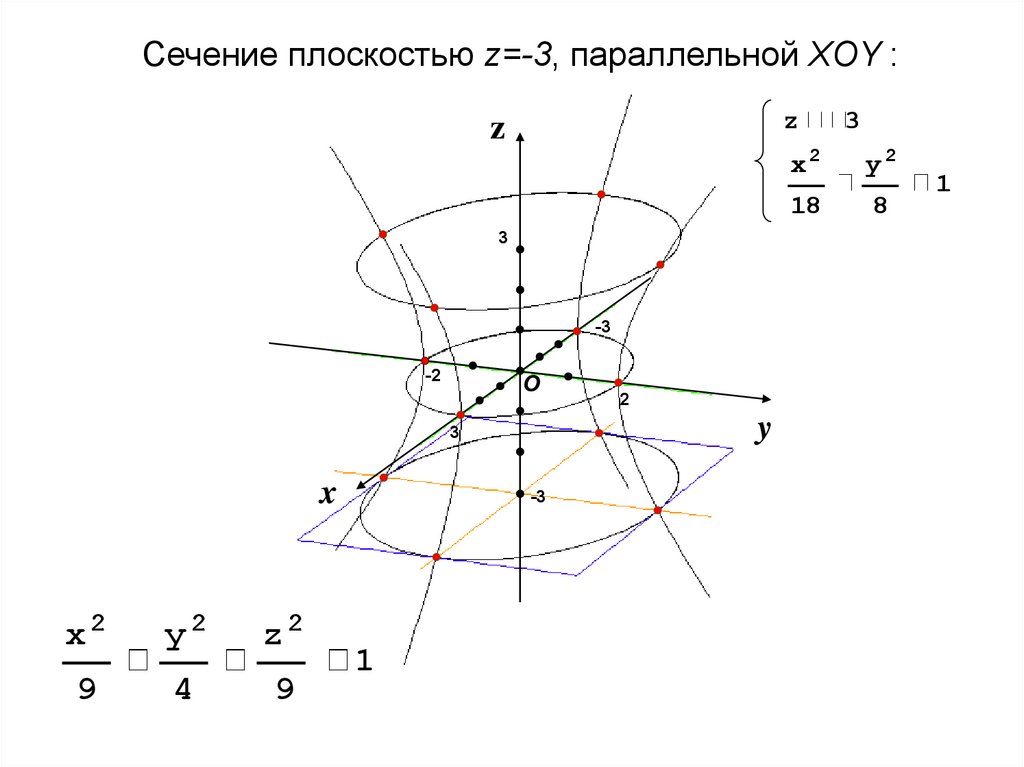
Сечение плоскостью z=-3, параллельной XOY :
z
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2
3
x2
y2
18
8
1

21.

Все сечения :
z
3
-3
-2
О
y
3
x
x2
y2
z2
9
4
9
-3
1
2