Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г

1.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 1. Начало
? сентября
1. Можно ли квадрат 1 × 1 обложить со всех сторон квадратами 10 × 10 вплотную к
нему без наложения?
2. В мешке 24 кг гвоздей. Как, имея только весы без стрелки, отмерить 9 кг гвоздей?
3. Червяк ползет по столбу, начав путь от его основания. Каждый день он проползет
вверх на 5 см, а за каждую ночь сползает вниз на 4 см. Когда он достигнет верхушки
столба, если его высота 10 см?
4. На книжной полке рядом слева направо стоят два тома Пушкина: первый и второй.
Страницы каждого тома имеют вместе толщину 2 см, а обложка - каждая - 2 мм.
Червь прогрыз (перпендикулярно страницам) от первой страницы первого тома до
последней страницы второго тома. Какой путь он прогрыз?
5. Петя говорит: позавчера мне было 10 лет, а в следующем году мне исполнится 13.
Может ли такое быть?
6. Пятиклассник выписал в свою тетрадь числа: 58, 59, 60, . . . , 630. Сколько чисел написал пятиклассник?
7. Разрежьте квадрат на треугольники так, чтобы каждый из треугольников граничил
ровно с тремя другими.
8. Можно ли на плоскости отметить 6 точек и соединить их непересекающимися отрезками (с концами в этих точках) так, чтобы из каждой точки выходило ровно по
4 отрезка?

2.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 2. Думаем и... еще раз думаем!
? сентября
1. Можно ли куб 1 × 1 × 1 обложить со всех сторон кубами 10 × 10 × 10 вплотную к
нему без наложения?
2. Пятиклассник выписал в свою тетрадь числа: 58, 59, 60, . . . , 630. Сколько цифр написал пятиклассник?
3. Из трех одинаковых по виду колец одно несколько легче других. Как найти его
одним взвешиванием на чашечных весах?
4. В стране Умсила 9 футбольных команд, причём между каждыми двумя было сыграно по одному матчу. Сколько всего было проведено матчей?
5. На сковородке одновременно можно жарить не более двух котлет. Одна сторона
котлеты жарится минуту. Как быстрее всего обжарить 3 котлеты с обеих сторон? А
как 2011?
6. Найти пятизначное натуральное число, записанное с помощью двоек и троек, у которого сумма и произведение цифр делятся на 6. А есть ли другие такие пятизначные
числа? А четырехзначные?
7. Четно или нечетно число 101 + 102 + 103 + 104 + · · · + 197 + 198 + 199 + 200?
8. На доске были написаны несколько первых натуральных чисел. Когда Вася стер
одно из них, сумма оставшихся оказалась равна 89. Какое число стер Вася?

3.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 3. Новая
? сентября
1. В одной 13-метровой комнате я обнаружил на полу три одинаковых ковра, каждый
площадью в 6 кв.м. Каждый перекрывался с каждым, и общая часть любых двух
ковров была равна 2 кв.м. А площадь той части пола, которая была покрыта всеми тремя коврами, оказалась равной 1 кв.м. Какая часть площади пола не была
покрыта ни одним ковром?
2. Имеется 19 каменных глыб весом 1,2 т каждая и 47 глыб весом 1,1 т каждая. Начальник станции хочет погрузить их в два вагона так, чтобы общий вес камней в
них был одним и тем же. Сможет ли он сделать это, не дробя камни?
3. Напишите наименьшее натуральное число, составленное из всех возможных различных цифр.
4. В классе имеется 5 различных ручек и 6 карандашей. Наташа пришла раньше всех:
Сколькими способами она может выбрать набор из ручки и карандаша?
5. В левом нижнем углу шахматной доски 5 × 5 стоит фишка. За один ход фишку
разрешается передвинуть на одну клетку вправо или вверх. В каждой клетке записывается число способов передвинуть фишку из начального положения в данную
клетку. Какое число записано в правом верхнем углу?
6. Разность двух целых чисел умножили на их произведение. Могло ли получиться
число 2011?
7. Можно ли из полосок 1 × 1, 1 × 2, . . . , 1 × 13 сложить прямоугольник со сторонами
больше 1?

4.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 4. Турниры и поместья
? сентября
1. В олимпийском турнире (проигравший выбывает) участвовало 199 команд. Сколько
матчей они сыграли?
2. Можно ли устроить такой тренировочный турнир, чтобы в нём участвовало 8 команд, и каждая в нём сыграла ровно 3 матча?
3. В футбольной команде (11 человек) нужно выбрать капитана и его заместителя.
Сколькими способами это можно сделать?
4. В кузнице есть 4 кузнеца. Каждый из них может подковать одну ногу лошади за
1 минуту. Одну лошадь одновременно могут подковывать не более одного кузнеца.
За какое наименьшее время эти кузнецы подкуют 4 лошади? а 5 лошадей? а 75?
5. В одной области страны Умсила живут 15 умсилачей. Некоторые из них поссорились друг с другом. Могло ли быть так, что каждый поссорился ровно с одним из
остальных?
6. Найдите хотя бы одно натуральное число, которое при умножении на 111 дает на
конце 2005.
7. В классе 14 человек занимаются музыкой, 8 рисованием, и 10 танцами. Трое - рисованием и танцами, четверо - рисованием и музыкой, а пятеро музыкой и танцами.
Одна только Юля посещает сразу всё. Сколько человек в классе, если известно, что
каждый ходит хотя бы на один кружок?
8. Поместья некоторых умсилачей, проживающих в стране Умсила, соединены между
собой дорогами. Заезжий путешественник обнаружил, что из поместья его друга
умсилача Соединялкина можно доехать до любого другого умсилача (быть может,
заезжая по дороге к кому-нибудь еще). Докажите, что из любого поместья в графстве можно проехать по дорогам в любое другое.

5.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 5.
3 октября
1. Первый день каникул был 12 марта, а последний - 24 мая. Сколько дней длились
каникулы?
2. На каждой перемене Заяц съедает по конфете. За неделю (с понедельника по субботу) было 30 уроков. Сколько всего конфет съел Заяц?
3. Найдите правило составления последовательности и вставьте пропущенное число:
а) 1, 3, 6, 10, * , 21, 28...
б) 1, 1, 1, 3, 5, 9, 17, * , 57 ...
в) 1, 3, 7, 13, 21, * , 43 ...
г) 5, 14, 41, 122, * , 1094 ...
4. Бикфордов шнур горит неравномерно и сгорает ровно за 1 минуту. Как при помощи
двух таких шнуров отмерить ровно 45 секунд?
5. Как посадить 9 деревьев так, чтобы получилось 10 прямых рядов по три дерева в
каждом?
6. Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама – за 2
минуты, малыш за 5 минут, а бабушка за 10 минут. У них есть один фонарик. Мост
выдерживает только двоих. Как им перейти мост за 17 минут? Если переходят двое,
то они идут с меньшей из их скоростей. Двигаться по мосту без фонарика нельзя.
Перебрасывать фонарик через реку нельзя. Светить издали нельзя. Носить друг
друга на руках нельзя.

6.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 6.
6 октября
1. Попугай Иннокентий знает следующие слова: филин, кот, таракан, поёт, бежит, стучит, спит, говорливый, мудрый, усатый. Он может произносить такие фразы:
прилагательное + существительное + глагол .
Например, «Мудрый таракан поёт». Сколько разных фраз может сказать Кеша?
2. Из четырех деталей одна отличается по весу от остальных, имеющих одинаковый
вес. Как выделить ее двумя взвешиваниями на весах с двумя чашками без гирь?
3. В турнире участвовало 10 команд, каждая в нём сыграла ровно 3 матча. Сколько
матчей они сыграли?
4. Отец с двумя сыновьями отправился в поход. На их пути встретилась река, у берега
которой находился плот. Он выдерживает на воде или отца, или двух сыновей. Как
переправиться на другой берег отцу и сыновьям?
5. Сколькими способами можно добраться от театра до харчевни, если можно двигаться только по стрелочкам:
6. Из магазина шла стройная колонна пятиклассников. У каждого в карманах пряники: сколько в правом кармане, столько и в левом. Могло ли у них вместе быть 2009
пряников?
7. Вставьте слово, пропущенное в скобках
ЙП (КРУГ) ФД
БН ( . . . . ) МЛ

7.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 7.
10 октября
1. Петя и Вася составляют четырехзначное число, записывая последовательно его цифры следующим образом: Петя пишет нечетные цифры, а Вася – 2 или 8. Начинает
Петя. Сколько различных четырехзначных чисел они могут выписать?
2. Сума пяти натуральных чисел нечетна. Сколько среди них могло быть нечетных
чисел?
3. В какой то момент турнира оказалось, что пять команд сыграло ровно по семь матчей, а семь команд – ровно по пять матчей. Сколько всего было проведено матчей,
если всего в турнире участвовало 12 команд?
4. Из трех монет одна фальшивая (отличается по весу от остальных, имеющих одинаковый вес). За какое наименьшее количество взвешиваний можно узнать – легче
она или тяжелее?
5. Паук ползет по своей паутине вниз. Сколькими способами он может добраться из
точки А в точку B?
6. Имеется два типа песочных часов. Одни отмеряют 7 минут, а другие – 11 минут.
Как с их помощью отмерить 15 минут?
7. Куб сложен из 27 одинаковых кубиков размерами 1 × 1 × 1. Из него вынули все
угловые кубики. Найдите площадь получившейся фигуры.
8. В агенстве работают несколько человек, причем каждый из них знает хотя бы один
иностранный язык: 6 человек знают английский, 7 – французский, 6 – немецкий,
4 знают английский и немецкий, 3 – немецкий и французский, 2 – французский и
английский, 1 человек знает все три языка. Сколько всего человек там работают?

8.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 8. Алексей вернулся :)
13 октября
1. Перед Алексеем на столе стоит 16 стаканов. Из них 15 стаканов стоят правильно, а
один перевернут донышком вверх. Алексей может одновременно перевернуть любые
два стакана (у него же две руки). Может ли он, повторяя эту операцию, поставить
все стаканы правильно?
2. Алексей заметил, что на кружке завелся школьник который всегда говорит правду
или всегда врет (но он не знает что точно). Мог ли этот школьник сказать: «Я всегда
вру».
3. Алексей пилил бревна. Он сделал 135 распилов и у него получилось 157 полена.
Сколько бревен у него было первоначально?
4. Смотря на ночное небо, Алексей заметил, что можно ввести космическое сообщение между 9 планетами Солнечной системы по следующим маршшрутам:
Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–
Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–
Уран. Можно ли в его воображении добраться с Земли до Марса?
5. Алексею нравиться число «2009». Сколькими различными способами он может составить это число начиная от цифры 2 в центре, двигаясь от кружка к кружку, если
они касаются друг друга.
6. Из 9 монет – 8 настоящих и одна фальшивая (все настоящие весят одинаково, фальшивая легче настоящей). Как Алексей может найти фальшивую за два взвешивания?
7. При хотьбе по шпалам Алексей может наступать или на следующую или через одну.
Сколькими способами Алексей может пройти с первой шпалы на тринадцатую?
8. Алексей наблюдал турнир по футболу. В какой то момент турнира оказалось, что
три команды сыграло ровно по семь матчей, пять команд — ровно по пять матчей, а
семь команд – ровно по три матча. Могло ли такое быть, если в турнире участвовало
ровно 15 команд?

9.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 9. Бароны и графы.
1. За круглым столом сидят 12 человек: лжецы (они всегда врут) и рыцари (они всегда
говорят правду). Каждый из сидящих за столом произнес: «Напротив меня сидит
лжец». Сколько лжецов за столом?
2. По дороге в город барон Мюнхаузен натолкнулся на двух островитян А и В. «Мы
оба лжецы!» - бодро сообщил А. Кто они?
3. Есть 12 монет, среди них ровно одна фальшивая, но неизвестно, тяжелее она или
легче, чем настоящая. Есть чашечные весы без гирь и стрелок. Можно ли найти
фальшивую монету за четыре взвешивания.
4. Барон Мюнхгаузен говорит, что, как бы ни стояли на шахматной доске 6 ладей,
не бьющих друг друга, он всегда сможет добавить еще коня так, чтобы ни одна из
фигур не била другую. Прав ли он?
5. На окружности отмечены 5 красных и 7 синих точек. Рассмотрим всевозможные
отрезки (хорды) с концами в отмеченных точках. У скольких отрезков концы а)
разного цвета; б) одинакового цвета?
6. Вернувшись с Луны на Землю, барон Мюнхгаузен рассказал, что у каждого из
живущих там 2003 лунатиков нечетное число рук. Барон похвастался, что в честь
его приезда все лунатики взялись за руки так, что свободных рук не осталось. Не
ошибается ли честный барон?
7. Докажите, что из любых трех целых чисел можно выбрать два, сумма которых
делится на два.

10.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 10. Логика, ничего кроме логики.
1. Островитянин A в присутствии другого островитянина В говорит: «По крайней мере
один из нас — лжец». Кто такой A и кто такой В?
2. Встретились несколько аборигенов, и каждый из них заявил всем остальным: «Вы
все — лгуны». Сколько рыцарей могло быть среди этих аборигенов?
3. Министру сообщили, что в партии из 101 монеты ровно 50 фальшивых, причем они
легче настоящих на 1 г. Министр выбрал из этих 101 монет одну. Как ему за одно
взвешивание на весах со стрелкой определить подлинность этой монеты?
4. На дверях появилось объявление: «Директор гимназии категорически возражает
против отмены решения о запрете контроля за причёсками». Может ли теперь Исмагил покрасить волосы в красный цвет без риска быть отчисленным?
5. На доске в классе написано число 23. Каждую минуту Вася стирает с доски написанное на ней число и записывает на его место произведение его цифр, увеличенное
на 12. Что окажется на доске через час?
6. Существуют ли 3 натуральных числа, попарные суммы которых равны а) 16, 17, 18;
б) 17, 18, 19?
7. В языке племени УЫУЫ всего две буквы – У и Ы. К тому же два слова, которые можно получить друг из друга перестановкой букв, всегда означают одно и
то же. Дикари племени называют всех животных словами из восьми букв. Какое
наибольшее количество животных они могут знать?

11.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 11. Ничего нового.
1. В строчку выписывают цифры по следующему правилу: первая цифра – 9, а каждые
две подряд стоящие цифры должны образовывать число, делящееся на 17 или 23.
Какая цифра может оказаться на 999-ом месте?
2. Вася приобрел дрессированного лягушонка, который умеет прыгать по прямой дорожке на 1 см вправо или влево. Может ли случиться так, что лягушонок сделает
ровно 25 прыжков и вернется в исходное положение?
3. Даны четыре одинаковых по виду шара массой 101 г, 102 г, 103 г и 104 г, а также
чашечные весы со стрелкой, на которых можно взвесить произвольный груз. Сделав
два взвешивания, определите массу каждого шара.
4. В стране Умсила, в округе Мозговитом проживают 15 джентльменов. Новый бариннаместник распорядился соединить их усадьбы дорогами так, чтобы усадьба каждого джентльмена была соединена дорогами ровно с пятью другими. Удастся ли
выполнить это распоряжение?
5. Из класса в 20 человек выбирают группу тех, кто пойдёт в театр. Число человек в
такой группе может быть любым от 0 до 20 человек. Каким числом способов можно
сделать такой выбор?
6. Докажите, что сумма пяти последовательных чисел делится на 5.
7. Алеша Попович и Добрыня Никитич воюют с девятиглавым змеем. По очереди
богатыри ходят к его пещере и отрубают 1, 2 или 3 головы. Как начавшему бой
Алеше обрести славу победителя змея (т.е. отрубить последнюю голову)? А если
змей двенадцатиглавый?

12.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 12. После каникул.
1. У Маши появилась пианино с а) 12 клавишами, б) 11 клавишами. Андрей и Артур
играют в игру по следующим правилам. Они по очереди отрывают 1 или 2 подряд
идущие клавиши. Проигрывает тот, кто не сможет сделать ход. Кто выигрывает при
правильной игре (т.е. кто выигрывает в не зависимости от ходов противника)?
2. Цифры от 0 до 9 выписали в строчку так, что среди любых трех подряд идущих
цифр сумма каких-то двух равна 7. Чему может быть равна сумма первой и последней цифр?
3. 7 карандашей стоит столько же сколько 8 ручек. Что стоит больше: ручка или
карандаш?
4. Предположим, что А высказывает утверждение: «Я лжец, а В не лжец». Кто из
островитян А и В рыцарь и кто лжец?
5. Из 4 монет одна фальшивая, но неизвестно, легче она или тяжелее настоящей. Кроме того, имеется одна заведомо настоящая монета. Можно ли за два взвешивания
определить фальшивую монету и выяснить, легче она или тяжелее?
6. Найти 10 натуральных чисел, сумма которых равна их произведению.
7. Какое наибольшее число не бьющих друг друга коней можно поставить на доску
8 × 8?

13.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 13. Еще 2 задачи
14 ноября
1. 1) Даны 2 кучки камней. В каждой кучке по 20 камней. За ход разрешается брать
любое количество камней из одной кучки. Проигрывает тот, кто не может сделать
хода. Кто имеет выигрышную стратегию?
2) Даны 2 кучки камней. В одной кучке 20 камней, в другой 10 камней. За ход
разрешается взять любое количество камней из одной кучки. Проигрывает тот, кто
не может сделать хода. Кто имеет выигрышную стратегию?
3) В левом нижнем углу шахматной доски стоит ладья. За один ход ее можно передвинуть на любое количество клеток вверх или вправо. Игрок поставивший ее в
правый верхний угол выигрывает. Кто из двух игроков выигрывает при правильной
игре?
4) Даны 2 кучки камней. В каждой кучке по 20 камней. За ход разрешается взять
2 камня из одной кучки и один из другой. Проигрывает тот, кто не может сделать
хода. Кто имеет выигрышную стратегию?
2. На одной из двух параллельных прямых выбрано 8 точек, а на другой - 6 точек.
1) Сколько можно построить отрезков, соединяющих две точки, лежащие на разных
прямых?
2) Пусть отрезок AB соединяет третью точку на первой прямой с четвёртой точкой
на второй. Сколько отрезков, соединяющих две точки, лежащие на разных прямых,
пересечёт отрезок AB внутри полосы?
3) Подсчитайте число отрезков с концами на второй прямой.
4) Сколько можно построить треугольников с вершинами на первой прямой и основаниями на второй?
5) Подсчитайте число отрезков с концами на первой прямой.
6) Сколько можно построить треугольников, у которых одна из вершин расположена
на одной прямой, а две других на другой?
7) Сколько можно построить четырёхугольников с вершинами в данных точках?
8) Подсчитайте общее число точек пересечения внутри полосы всех отрезков с концами на двух прямых, считая, что никакие три отрезка не пересекаются в одной
точке.

14.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 14.
17 ноября
1. Дима старше Вани, Ваня старше Марины. Кто старше: Дима или Марина?
2. Три мальчика – Миша, Сережа и Гриша – живут в одном подъезде на разных этажах
– 5, 7, 8. Миша живет не ниже Гриши, а Сережа не выше Гриши. Кто где живет?
3. В четырехэтажном доме Ваня живет выше Пети, но ниже Кати, а Вася живет ниже
Пети. Кто на каком этаже живет?
4. Ложка тяжелее, чем вилка, а нож легче, чем ложка. Что легче всего?
5. Врач прописал Вам таблетки двух сортов: А и В. Вы должны принимать две таблетки одновременно через каждые пол часа: одну таблетку сорта А и одну таблетку
сорта В. Именно в таком сочетании сортов и количеств лекарства, иначе могут быть
нежелательные последствия. Но вот беда: когда осталось всего два приема, 4 таблетки перемешались (из них две таблетки сорта А и 2 таблетки сорта В) различить
эти таблетки по внешнему виду совершенно невозможно. Что делать?
6. Квадратный лист бумаги сложили а) два б) четыре раза пополам и получили квадрат. Этот квадрат разрезали по обеим диагоналям. На сколько частей распался лист
бумаги?
7. Дети, построенные парами, выходят из лесу, где они собирали орехи. В каждой паре
идут мальчик и девочка, причём у мальчика орехов либо вдвое больше, либо вдвое
меньше, чем у девочки. Могло ли так случиться, что у всех детей вместе было 1000
орехов?
8. Назовем натуральное число «симпатичным», если в его записи встречаются только
нечетные цифры. Сколько существует четырехзначных «симпатичных» чисел?
9. Алфавит племени Мумбо-Юмбо состоит из трех букв А, Б и В. Словом является
любая последовательность, состоящая не более, чем из 4 букв. Сколько слов в языке
племени Мумбо-Юмбо?

15.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 15. Солянка
21 ноября
1. В общежитии в одной комнате живут четыре девушки: Маша, Валя, Таня и Галя.
Две из них ровесницы. Известно, что Таня старше Маши, которая моложе Гали.
Таня моложе Вали, которая старше Гали. Кто ровесницы?
2. Дядя Федор, кот Матроскин, Шарик и почтальон Печкин сидят на скамейке. Если
Шарик, сидящий справа от всех, сядет между дядей Федором и котом, то кот станет
крайним слева. В каком порядке они сидят?
3. Число x – натуральное. Из утверждений 2x>70, x<100, 3x>25, x>10 и x>5 три
верных и два неверных. Чему равно x?
4. Илья Муромец, Добрыня Никитич и Алеша Попович вступили в бой с несколькими
великанами. Каждый великан получил по 3 удара богатырскими палицами, в результате чего все великаны обратились в бегство. Больше всего ударов нанес Илья
Муромец – 7, меньше всего Алеша Попович – 3. Сколько всего было великанов?
5. Предание гласит, что в некоторой стране есть озера, соединённые между собой реками. Из каждого озера вытекает 3 реки, и в каждое озеро впадают 2 реки. Можно
ли верить этому преданию?
6. Имея полный бак топлива, катер может проплыть 72 км против течения реки или
120 км по течению. На какое наибольшее расстояние по реке он может отплыть при
условии, что он должен вернуться?
7. В Межпланетном Шахматном Турнире участвовал 101 игрок. Оказалось, что каждый выиграл 50 партий, причём любые двое сыграли не более одной партии. Сколько
партий проиграл каждый игрок?
8. В алфавите 22 согласных и 10 гласных букв. Сколько можно составить двухбуквенных слов со следующими условиями:
1) Первая буква согласная, а вторая - гласная.
2) Одна из двух букв согласная, а другая гласная, но буквы стоят в любом порядке.
3) Никаких ограничений на буквы не накладывается.
4) Обе буквы одинаковые.
5) Обе буквы разные.
6) Первая буква гласная, а вторая - произвольная.
7) Хотя бы одна буква - гласная.
8) Либо обе буквы гласные, либо обе согласные, но при этом разные.

16.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 16. Винегрет
24 ноября
1. В соревнованиях по бегу участвуют 10 спортсменов: Андрей, Виктор, Ефим, Захар,
Иван, Клим, Михаил, Николай, Тимофей и Федор. Спортсмен, первым пришедший к
финишу, получил 9 баллов, вторым – 8 баллов, третьим – 7 и т.д., вплоть до последнего, который получил 0 баллов. Как распределились баллы между участниками
бега отражено ниже:
Клим пришел к финишу позже Виктора.
Ефим пришел к финишу раньше Тимофея.
Николай пришел к финишу позже Федора.
Захар пришел к финишу позже Андрея.
Михаил пришел к финишу раньше Ефима.
Иван пришел к финишу позже Клима.
Николай пришел к финишу раньше Виктора.
Захар пришел к финишу раньше Михаила.
Иван пришел раньше Андрея.
Определите, сколько баллов получил каждый из 10 спортсменов.
2. Заменить буквы в слове «транспортировка» цифрами (одинаковые буквы одинаковыми цифрами, разные – разными) так, чтобы выполнилось неравенство:
Т>Р>А>Н<С<П<О<Р<Т>И>Р>О<В<К<А.
3. Существует ли трехзначное число, делящееся на 11, у которого первая цифра больше
второй, а вторая больше третьей?
4. На шахматной доске стоят белые пешки. Докажите, что найдётся пешка, которую
ни одна другая не бьёт(пешка бьёт на одну клетку по диагонали вверх).
5. На шахматной доске стоит несколько ладей. Докажите, что какая-то из ладей бьет
не более двух других.
6. На шахматной доске стоит несколько ферзей. Обязательно ли найдется ферзь, бьющий не более трех других?
7. Сколькими способами можно замостить доминошками поле на рисунке? (доминошки не могут перекрываться, чёрные клетки замощать нельзя)

17.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 17. Винигрет 2. Возвращение неравенства
12 декабря
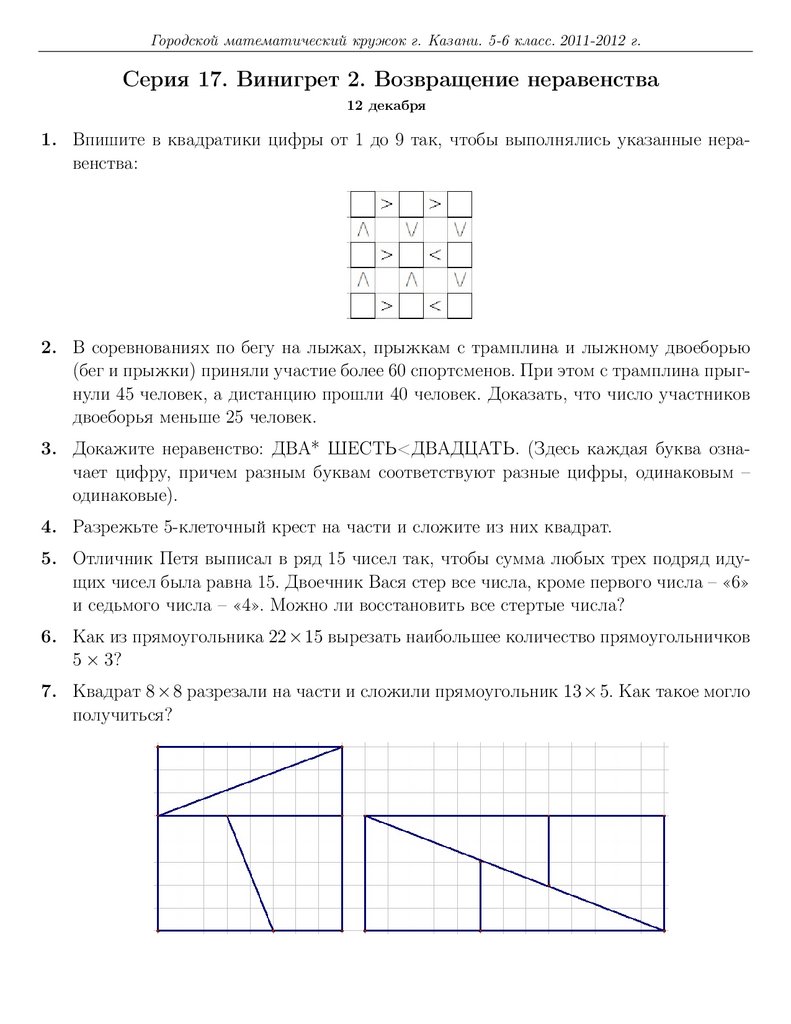
1. Впишите в квадратики цифры от 1 до 9 так, чтобы выполнялись указанные неравенства:
2. В соревнованиях по бегу на лыжах, прыжкам с трамплина и лыжному двоеборью
(бег и прыжки) приняли участие более 60 спортсменов. При этом с трамплина прыгнули 45 человек, а дистанцию прошли 40 человек. Доказать, что число участников
двоеборья меньше 25 человек.
3. Докажите неравенство: ДВА* ШЕСТЬ<ДВАДЦАТЬ. (Здесь каждая буква означает цифру, причем разным буквам соответствуют разные цифры, одинаковым –
одинаковые).
4. Разрежьте 5-клеточный крест на части и сложите из них квадрат.
5. Отличник Петя выписал в ряд 15 чисел так, чтобы сумма любых трех подряд идущих чисел была равна 15. Двоечник Вася стер все числа, кроме первого числа – «6»
и седьмого числа – «4». Можно ли восстановить все стертые числа?
6. Как из прямоугольника 22×15 вырезать наибольшее количество прямоугольничков
5 × 3?
7. Квадрат 8 × 8 разрезали на части и сложили прямоугольник 13 × 5. Как такое могло
получиться?

18.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 18. Солянка 2
15 декабря
1. Лифт поднимается на 7 этаж за 42 секунды. За сколько времени тот же лифт поднимется на 11 этаж?
2. Бочку можно наполнить, если в нее налить 6 маленьких, 3 средних и 1 большое
ведро воды, или 2 маленьких, 1 среднее и 3 больших ведра воды. А сколько только
больших ведер потребуется для наполнения бочки?
3. Дно квадратного бассейна выложено квадратными плитками двух цветов, как показано на рисунке. Всего использовано 10000 плиток. На сколько больше понадобилось
светлых плиток, чем темных?
4. Можно ли квадрат 4 × 4 без угловой клетки (см. рис.) разрезать на 3 равные части?
5. В таблице 3 × 3 расставлены натуральные числа (смотри рисунок). Коля и Петя вычеркнули по четыре числа. Оказалось, что сумма чисел, вычеркнутых Петей, втрое
больше, чем сумма чисел, вычеркнутых Колей. Какое число оказалось невычеркнутым?
4 12 8
13 24 14
7 5 23
6. Коля и Миша разрезали два одинаковых прямоугольника (каждый свой). У Коли
получились 2 прямоугольника, каждый периметром 40см, а у Миши 2 прямоугольника, каждый периметром 50см. Какой периметр имели первоначальные прямоугольники?

19.

Городской математический кружок г. Казани. 5-6 класс. 2011-2012 г.
Серия 19. Теорема Пифагора
19 декабря
1. Разрежьте квадрат 7 × 7 на
а) квадраты 4 × 4, квадрат 3 × 3 и 4 равных прямоугольных треугольника;
б) один квадрат и 4 прямоугольных треугольника, равных треугольникам из (а);
в) Найдите размер квадрата в (б).
2. Даны 4 прямоугольных треугольника с катетами a, b и гипотенузой c. Докажите,
что добавив к ним а) один квадрат со стороной c; б) два квадрата со сторонами a и
b, можно будет составить квадрат со стороной a + b.
3. (Теорема Пифагора) a2 + b2 = c2 .
4. Разрежьте квадрат на равные квадраты из которых составьте два различных квадрата.
Определение. Перекроить = разрезать на части и сложить из них.
5. Перекроите квадрат в 8 равных квадратов.