Similar presentations:
Математический турнир для 5-6 классов
1.
Математическийтурнир для 5-6 классов
Топкаева
Галина Геннадьевна
2.
Задача 1Какое наименьшее 10-значное число можно получить, по-разному
записывая шесть чисел 316, 3, 21, 6, 83, 7 одно за другим?
3.
Задача 1Какое наименьшее 10-значное число можно получить, по-разному
записывая шесть чисел 316, 3, 21, 6, 83, 7 одно за другим?
Ответ
Решение: 21 316 3 6 7 83
4.
Задача 2В забеге принимал участие 61 спортсмен. Раньше Дениса прибежало в 5
раз меньше спортсменов, чем позже него. Какое место на соревнованиях
занял Денис?
5.
Задача 2В забеге принимал участие 61 спортсмен. Раньше Дениса прибежало в 5
раз меньше спортсменов, чем позже него. Какое место на соревнованиях
занял Денис?
Ответ
Пусть до Дениса прибежало х спортсменов, тогда после него прибежало
5х спортсменов. Зная, что всего участников 61, составим уравнение:
х+5х+1=61. Откуда х=10. Значит Денис занял 11 место
6.
Задача 3Как гномам разложить 7 алмазов в 4 одинаковые шкатулки, чтобы вес всех
шкатулок был одинаковым, если вес алмазов 1, 2, 3, 4, 5, 6, 7 граммов.
7.
Задача 3Как гномам разложить 7 алмазов в 4 одинаковые шкатулки, чтобы вес всех
шкатулок был одинаковым, если вес алмазов 1, 2, 3, 4, 5, 6, 7 граммов.
Ответ
1)1+2+3+4+5+6+7=28 граммов - вес всех алмазов,
2)28:4=7(г) – вес одной шкатулки,
3) 7=2+5=3+4=1+6
8.
Задача 4Сколько можно получить различных четырёхзначных чисел, вставляя
пропущенные цифры в число *2*5?
9.
Задача 4Сколько можно получить различных четырёхзначных чисел, вставляя
пропущенные цифры в число *2*5?
Ответ
На первом месте может стоять любая цифра кроме 0, то есть всего 9
различных цифр. На месте второй звездочки можно поставить 10
различных цифр, то есть всего 10 различных вариантов. Получаем всего
9*10=90 вариантов.
10.
Задача 5Пятиклассник Петя заметил, что если записать дату его рождения
восемью цифрами: сначала двумя цифрами число, двумя числами месяц и
потом четырьмя цифрами год, то это число будет читаться одинаково и
слева-направо, и справа-налево. А в записи будут использованы всего
различные 2 цифры. Запишите полную дату рождения Пети.
11.
Задача 5Петя заметил, что если записать дату его рождения восемью цифрами:
сначала двумя цифрами число, двумя числами месяц и потом четырьмя
цифрами год, то это число будет читаться одинаково и слева-направо, и
справа-налево. А в записи будут использованы всего различные 2 цифры.
Запишите полную дату рождения Пети.
Ответ
20.02.2002 (20 февраля 2002 г.)
12.
Задача 6В викторине по математике было всего 26 вопросов. За каждый
правильный ответ начисляется 8 очков, а за каждый неправильный ответ
снимается 5 очков. Аня решила проверить свои знания. После всех
ответов она подсчитала свои очки, и оказалось, что сумма равна нулю.
Сколько правильных и сколько неправильных ответов дала Аня?
13.
Задача 6В викторине по математике было всего 26 вопросов. За каждый
правильный ответ начисляется 8 очков, а за каждый неправильный ответ
снимается 5 очков. Аня решила проверить свои знания. После всех
ответов она подсчитала свои очки, и оказалось, что сумма равна нулю.
Сколько правильных и сколько неправильных ответов дала Аня?
Ответ
1) 26*8=208(оч.) – можно было заработать всего;
2) 8+5=13(оч.) – теряла Аня за 1 неправильный ответ, так как не только
теряла 5 очков, но и не получала за правильное решение 8 очков;
3) 208:13=16(в.) – не решила Аня
4) 26-16=10(в.) – решила Аня.
14.
Задача 7Электронные часы показывают время; часы двумя цифрами, минуты двумя цифрами, секунды – двумя цифрами. Укажите наибольшую
возможную сумму цифр, одновременно показываемых часами. Ответ
объясните.
15.
Задача 7Электронные часы показывают время; часы двумя цифрами, минуты двумя цифрами, секунды – двумя цифрами. Укажите наибольшую
возможную сумму цифр, одновременно показываемых часами. Ответ
объясните.
Ответ
Часы могут быть записаны от 00 до 24. Самая большая сумма цифр у числа
19. Минуты и секунды – от 00 до 60. Самая большая сумма цифр у числа
59. Получаем 19:59:59. Сумма цифр равна 38.
16.
Задача 8В классе 15 человек. Известно:
1) Каждый, кто принёс циркуль, принёс и линейку;
2) Забыли циркуль 9 человек, забыли линейку 4 человека.
Каких учеников больше: тех, кто принёс линейку или тех, кто принес
линейку, но забыл циркуль?
17.
Задача 8В классе 15 человек. Известно:
1) Каждый, кто принёс циркуль, принёс и линейку;
2) Забыли циркуль 9 человек, забыли линейку 4 человека.
Каких учеников больше: тех, кто принёс линейку или тех, кто принес
линейку, но забыл циркуль?
Ответ
15-9=6 человек принесли циркуль. Те, кто забыл линейку, забыли и
циркуль, - таких 4. Тех, кто принесли линейку, но забыли циркуль 9-4=5
(от забывших циркуль «отнимаем» забывших и циркуль, и линейку). Таким
образом, больше тех, кто принес циркуль (6>5).
18.
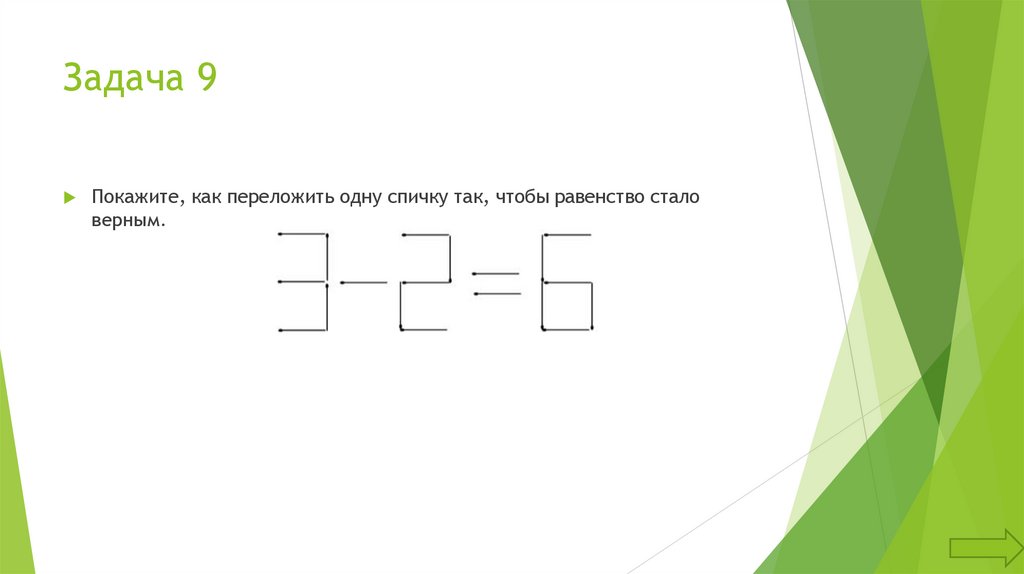
Задача 9Покажите, как переложить одну спичку так, чтобы равенство стало
верным.
19.
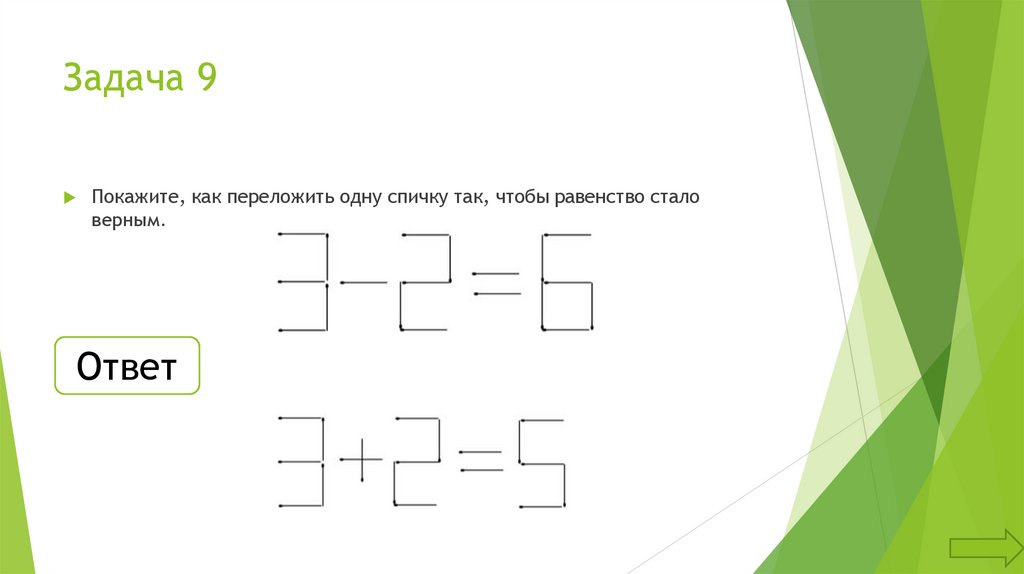
Задача 9Покажите, как переложить одну спичку так, чтобы равенство стало
верным.
Ответ
20.
Задача 10Задумано трехзначное число, у которого с любым из числе 543, 142 и 562
совпадает один из разрядов, а другие два не совпадают. Какое число
задумано?
21.
Задача 10Задумано трехзначное число, у которого с любым из числе 543, 142 и 562
совпадает один из разрядов, а другие два не совпадают. Какое число
задумано?
Ответ
Так как у числа совпадает одна цифра из разрядов чисел 543, 142 и 562, а
две другие не совпадают, то цифры 5, 4 и 2 не подходят. Остаются цифры
1, 6, 3. Получаем число 163.
22.
Задача 11Роскошно липа расцвела.
Под ней червяк завелся малый,
Да вверх пополз во всю он мочь –
Четыре локтя делал в ночь,
Но днем сослепу полз обратно
Он на два локтя аккуратно.
Трудился наш червяк отважный,
И вот итог работы важной,
Награда девяти ночей:
Он на верхушке липы сей.
Теперь, мой друг, поведай ты,
Какой та липа высоты.
23.
Задача 11Ответ
Роскошно липа расцвела.
Под ней червяк завелся малый,
Да вверх пополз во всю он мочь –
Четыре локтя делал в ночь,
Но днем сослепу полз обратно
Он на два локтя аккуратно.
Трудился наш червяк отважный,
И вот итог работы важной,
Награда девяти ночей:
Он на верхушке липы сей.
Теперь, мой друг, поведай ты,
Какой та липа высоты.
В первую ночь червяк поднялся на
высоту в 4 локтя, во вторую достиг
отметки в 6 локтей (на 2 локтя днём
сполз, и на 4 поднялся ночью), т.е. со
второй ночи он поднимался всякий раз
на 2 локтя и, таким образом за 9 ночей
оказался на высоте
4+2*8=20 локтей. Высота липы – 20
локтей.
24.
Задача 12Саша купил в универмаге товаров на 127 рублей. Хотя у Саши были только
пятирублевые монеты, а у кассира только двухрублевые, Саша сумел
расплатиться с кассиром. Каково наименьшее количество монет, которое
могло быть у Саши?
25.
Задача 12Саша купил в универмаге товаров на 127 рублей. Хотя у Саши были только
пятирублевые монеты, а у кассира только двухрублевые, Саша сумел
расплатиться с кассиром. Каково наименьшее количество монет, которое
могло быть у Саши?
Ответ
Заметим, что у Саши было больше 127 рублей. Пусть у него было х руб.,
тогда х-127 руб. ему дали сдачу. Так как сдачу ему дали только
двухрублёвыми монетами, то эта разность чётна, а значит, х наименьшее
нечетное число кратное 5. Этому условию удовлетворяет число 135.
Значит у Саши было 27 пятирублевых монет.
26.
Задача 13Как 9 деревьев посадить в 8 рядов, чтобы в каждом ряду было по 3
дерева?
27.
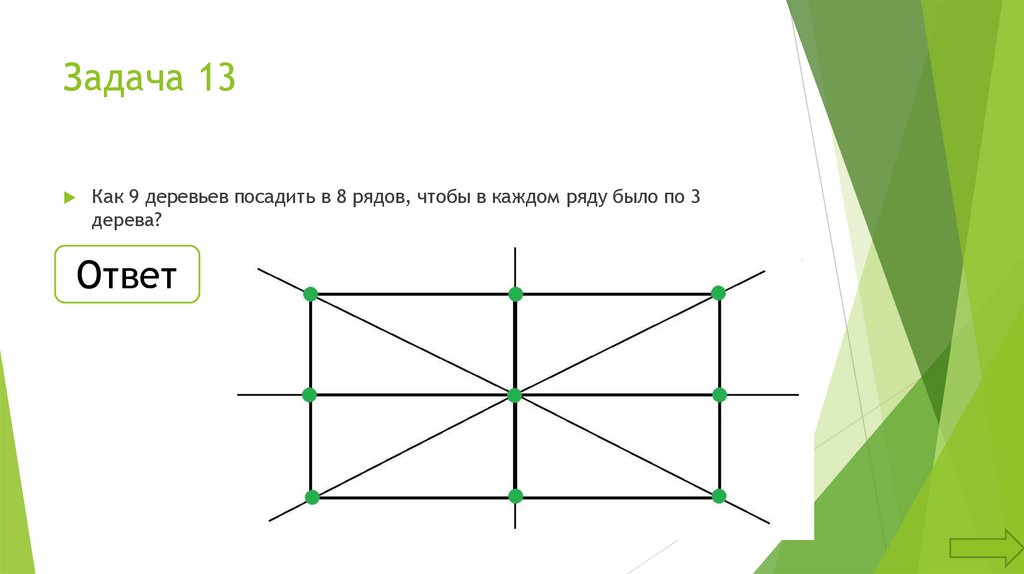
Задача 13Как 9 деревьев посадить в 8 рядов, чтобы в каждом ряду было по 3
дерева?
Ответ
28.
Задача 14Девять осликов за 3 дня съедают 27 мешков корма. Сколько корма надо 5
осликам на 5 дней?
29.
Задача 14Девять осликов за 3 дня съедают 27 мешков корма. Сколько корма надо 5
осликам на 5 дней?
Ответ
1) 27:3=9 мешков съедают 9 осликов за день;
2) 9:9=1 мешок съедает один ослик за один день;
3) 5*1=5 мешков съедает 5 осликов за один день;
4) 5*5=25 мешков съедают 5 осликов за 5 дней.
Итого 25 мешков.
Завершить


























 mathematics
mathematics








