Similar presentations:
Математическая викторина для обучающихся 5-6 классов
1. «Математическая викторина для обучающихся 5-6 классов» Автор: Табачкова В.Е. учитель математики МБОУ «Зубово-Полянская ООШ»
2. Угадайте закономерность и заполните пропуски
VIIIVII
XII
XIV
XI
XIII
XXV
XV
XXIV
XXX
XCVI
3.
Составь выражение и найди его значениеКод
А
Б
В
Г
Д
Е
Ж
З
И
К
Математическая модель
Л
7 кл.
М
7 кл.
Н
7 кл.
5 кл. Сумма произведения 13 и 4 и частного 100 и 25
5 кл. Частное суммы чисел 49 и 98 и произведения 3 и 7
5 кл. Разность произведения 7 на 15 и произведения 17 на 3
5 кл. Произведение частного 36 и 3 и разности 100 и 92
5 кл. Произведение числа 100 и суммы чисел 8 и 7
5 кл. Произведение разности чисел 57 и 42 и числа 1000
6 кл. Сумма произведения чисел 15 и 2 и частного чисел 42 и 6
6 кл. Разность частного чисел 270 и 3 и произведения чисел 25 и 3
6 кл. Частное суммы чисел 32 и 24 и числа 7
7 кл
4.
Составь выражение и найди его значениеКод
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
Выражение
13х4 + 100:25 = 52+4=56
(49+98) : (3х7) = 147 :21 = 7
7х15 - 17х3 = 105 – 51 = 54
36:3 х (100-92) = 12 х 8 = 96
100 х (8+7)= 1500
(57-42) х 1000 = 15000
15х2 + 42:6 = 37
270:3 - 25х3 = 90 – 75 = 15
(32+24): 7 = 56:7 = 8
3⅓ +2,5 х 16 = 3⅓ + 40 = 43⅓
2⅟7 х 24/5 - 2,4 = 6 - 2,4 = 3,6
(2,4+5,6)х (2,4-5,6) = 8 х (-3,2) = -25,6
2⅓+ 2,4 х 15 = 38⅓
5. Решите задачи:
В вольере сидят фазаны и кролики.Всего у них 12 голов и 34 ноги. Сколько
фазанов и сколько кроликов в
вольере?
6. Решение задач.
В вольере сидят фазаны и кролики. Всего у них 12 голов и 34 ноги. Сколькофазанов и сколько кроликов в вольере?
Фазаны – х шт. ; кролики – у шт.
Всего фазанов и кроликов х+у =12 (по количеству голов)
У фазанов 2х ног, а у кроликов - 4у ног, у всех вместе - 2х + 4у = 34 (н.)
х+у =12
2х + 4у = 34
х = 12 –у
2(12-у) +4у = 34
24 – 2у + 4у = 34
24 + 2у = 34
2у = 34 – 24
2у = 10
у=5
Ответ: 7 фазанов, 5 кроликов.
х = 12 – у = 12 – 5 = 7
7. Решение задач.
Петухи – х шт, поросята – у шт. Всего х + у = 11 (по кол-ву хвостов)У петухов – 2х ног, а у поросят – 4у ног, всего 2х + 4у = 30.
х+у =11
х = 11 – у
х = 11 –у = 11 – 4 = 7
2х+4у = 30
2(11-у) + 4у = 30
22-2у +4у = 30
22+2у = 30
2у = 30-22
2у = 8
у=4
Ответ: 7 петухов, 4 поросенка.
8. Шифровка
• Алена составила слово из 8 кубиков. На однойстороне каждого кубика – буква, а на другой –
порядковый номер этой буквы в алфавите. Ее брат
Ваня перевернул кубики числами вверх,
перемешал их и предложил младшей сестренке
Кате разгадать слово. Помогите Кате восстановить
слово: 10 24 14 6 20 18 6 5
• Карлсон составил слово из 8 кубиков. На одной
стороне каждого кубика – буква, а на другой –
порядковый номер этой буквы в алфавите. Малыш
перевернул кубики числами вверх, перемешал их и
предложил домоуправительнице разгадать слово.
Помогите домоуправительнице восстановить
слово: 10 12 14 6 20 18 16 13
9.
Отгадка:10 24 14 6 20 18 6 5
И Ц М Е Т И Е Д
А1
Б2 В3
Г4
Д5
Е6
Ж8
З9
Н 15
О 16 П 17 Р 18 С 19 Т 20
И 10 Й 11 К 12 Л 13
Ф 22 Х 23 Ц 24 Ч 25 Ш 26 Щ 27
Ы 29 Ь 30 Э 31 Ю 32 Я 33
Ё7
М 14
У 21
Ъ 28
10.
Отгадка:10 12 14 6 20 18 16 13
и к ме т р о л
А1
Б2 В3
Г4
Д5
Е6
Ж8
З9
Н 15
О 16 П 17 Р 18 С 19 Т 20
И 10 Й 11 К 12 Л 13
Ф 22 Х 23 Ц 24 Ч 25 Ш 26 Щ 27
Ы 29 Ь 30 Э 31 Ю 32 Я 33
Ё7
М 14
У 21
Ъ 28
11.
45
1
2
3
5
6
1
Кроссворды
«Определени
я»
2
3
4
12.
45
Кроссворд
«Определения»
6
1
2
3
1. Раздел математики,
посвященный изучению свойств
фигур.
13.
45
Кроссворд
«Определения»
6
1 г е ометр и я
2
3
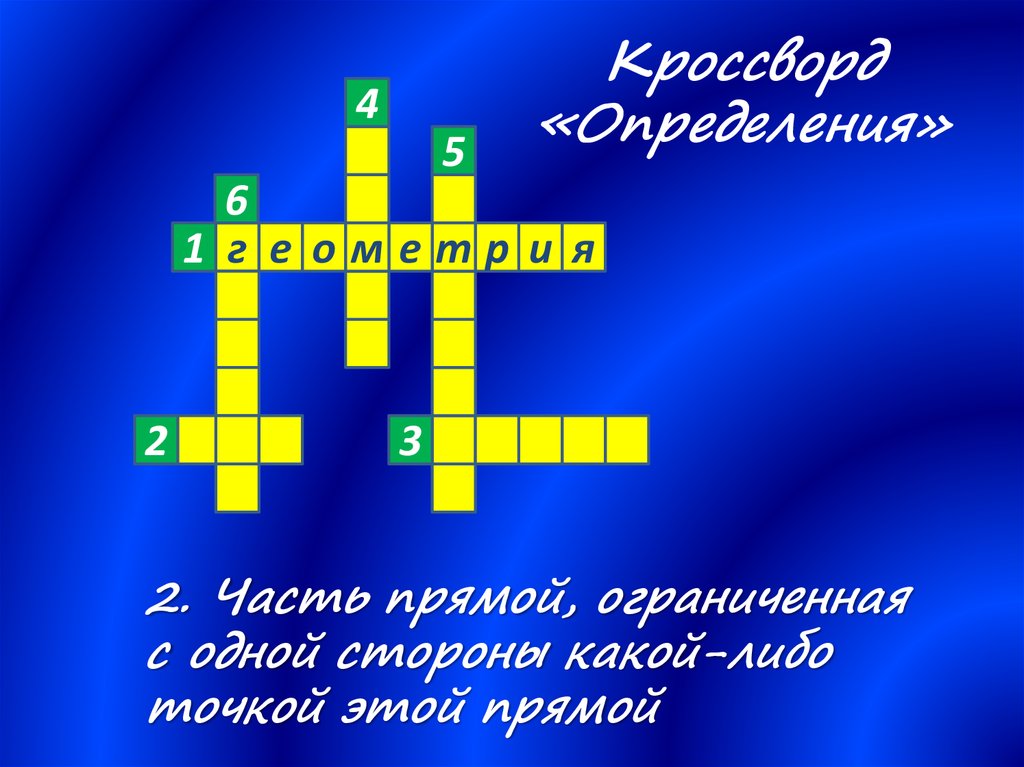
2. Часть прямой, ограниченная
с одной стороны какой-либо
точкой этой прямой
14.
45
Кроссворд
«Определения»
6
1 г е ометр и я
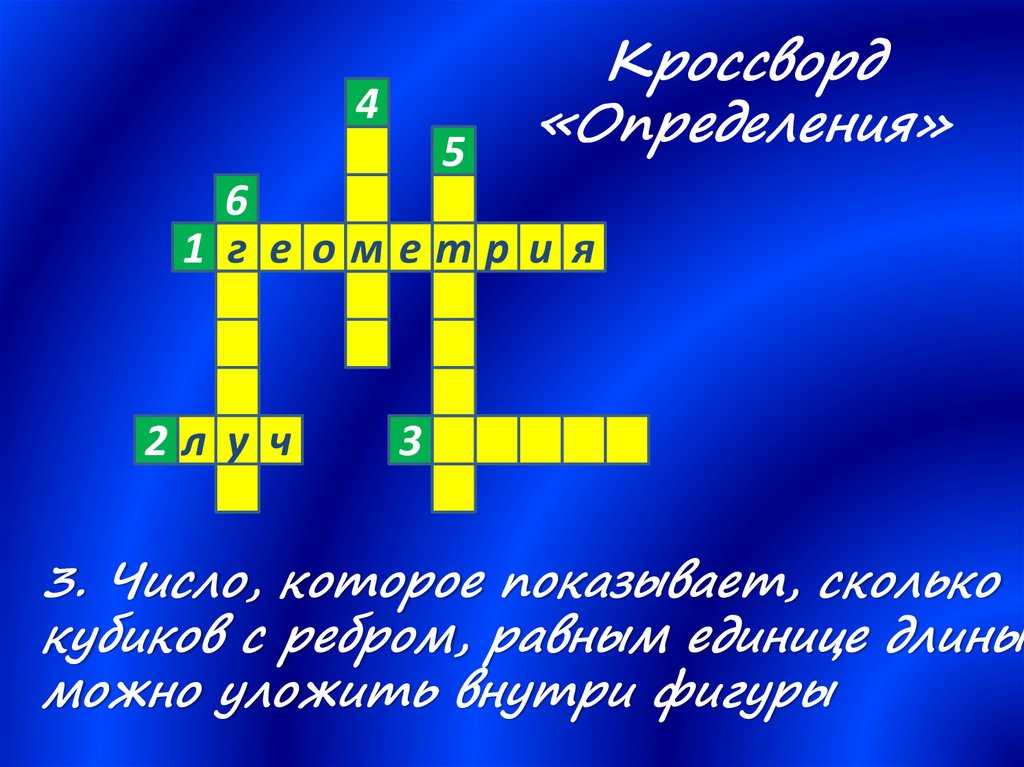
2л у ч
3
3. Число, которое показывает, сколько
кубиков с ребром, равным единице длины,
можно уложить внутри фигуры
15.
45
Кроссворд
«Определения»
6
1 г е ометр и я
2л у ч
3 о б ъ ем
4. Результат сложения двух чисел
16.
Кроссворд«Определения»
4
с 5
6
у
1 г е ометр и я
м
а
2л у ч
3 о б ъ ем
5. Все точки прямой, расположенные
между какими-либо двумя точками
этой прямой, и сами эти две точки
17.
Кроссворд«Определения»
4
с 5
6
у о
1 г е ометр и я
м р
а е
з
2л у ч
3 о б ъ ем
к
6. Величина, равная 1/180
развернутого угла
18.
Кроссворд«Определения»
4
с 5
6
у о
1 г е ометр и я
р
м р
а
а е
д
з
2л у ч
3 о б ъ ем
с
к
Молодцы!
19.
56
Кроссворд
«Определения»
1
2
3
4
1. Фигура, образованная двумя лучами,
имеющими общее начало.
20.
51
у
г
о
6
Кроссворд
«Определения»
л
2
3
4
2. Число, которое показывает, сколько
квадратов со стороной, равной единице
длины можно уложить внутри фигуры.
21.
51
у
г
о
6
Кроссворд
«Определения»
о
щ
л
2
п
л
а
д
ь
3
4
3. Равенство, из которого находят
неизвестную величину.
22.
51
у
г
3
о
у
6
Кроссворд
«Определения»
щ
л
р
2
п
л
о
а
в
н
е н
а
д
и
е
ь
4
4. Результат действия вычитания.
23.
51
у
4
г
о
6
Кроссворд
«Определения»
щ
л
2
п
л
о
3
у
р
а
в
н
е н
р
а
з
н
о
с
т
а
д
и
е
ь
ь
5. Правило вычисления значения какой –
либо величины.
24.
1у
г
3
4
р
5
ф
о
р
м
у
л
а
6
Кроссворд
«Определения»
щ
л
2
п
л
о
р
а
в
н
е н
з
н
о
с
т
а
д
и
е
ь
6. Одна сотая часть числа.
ь
25.
1у
г
3
4
р
5
ф
о
р
м
у
л
а
л
2
п
л
р
а
в
н
з
н
о
с
Кроссворд
6
п «Определения»
р
о щ а д ь
ц
е н и е
н
т ь
Молодцы!
























 mathematics
mathematics








