Основные сведения теории погрешностей геодезических измерений

1. Лекция Основные сведения теории погрешностей геодезических измерений

2. Теория погрешностей

1.Введение.
2.Виды геодезических измерений.
3.Классификация ошибок измерений.
4.Случайные погрешности.
5. Арифметическая средина.
6. Средняя квадратическая погрешность
функций измеренных величин.

3. Теория погрешностей

Теория погрешностей измерений
базируется на теории вероятностей и
математической статистике.
В теории погрешностей измерений решают
следующие задачи:
1.Изучение причин возникновения ощибок
измерений; изучение свойств ошибок
измерений и исследование законов
распределения их вероятностей

4. Теория погрешностей

2.Опредение наиболее надежных значений
искомых величин из результатов их
многократных, независимых равноточных и
неравноточных измерений.
3. Оценка точности непосредственно
выполненных результатов измерений и
предвычисление ожидаемой точности функций
измеренных величин.
4. Установление допусков, ограничивающих
использование результатов измерений в
заданных пределах точности.

5. Виды геодезических измерений

Измерить величину - значит сравнить
ее с другой, одноименной величиной,
принятой за единицу меры.
Измерения, в результате которых
определяется взаимное положение
точек местности, называют
геодезическими измерениями.
Геодезические измерения делятся на
необходимые и добавочные.

6. Все три вида геодезических измерений по точности делятся на высокоточные, средней точности и технической точности.

Все геодезические измерения можно разделить на 3 вида:
угловые, линейные и высотные.
Виды
геодезических
измерений
Высокоточные
Средней точности
Технической
точности
Угловые
измерения, ср. кв.
погрешность
0,5 3,0
3,0 10,0
10,0 30,0
1
1
1000000 100000
1 1
100000 5000
1 1
5000 200
0,5мм 5,0 мм 5мм 25,0 мм
25 мм и более
Линейные
измерения,
относительная
погрешность
Высотные
измерения, ср. кв.
погрешность на 1
км хода

7. Классификация погрешностей геодезических измерений, свойства случайных погрешностей

Погрешность измерения определяется:
l Х
l - измеренное значение величины
X - истинное значение
Δ - абсолютная истинная погрешность
Погрешности делятся на:
грубые
систематические
случайные

8. Классификация погрешностей геодезических измерений, свойства случайных погрешностей

Грубые погрешности – промахи, просчеты при измерениях.
Выявляются и устраняются повторными измерениями, в геодезии
измерения выполняются не менее двух раз.
Систематические погрешности- погрешности знаком и величиной
однообразно повторяющиеся при многократных измерениях.
Появляются
вследствие
неточной
установки
инструмента,
неисправности измерительных приборов, влияния внешней среды.
Их влияние можно частично исключить введением поправок.
Случайные погрешности возникают под влиянием многих
переменных факторов. Их величина и знак не остаются постоянными
и заранее не могут быть определены, исключить их из результатов
измерения невозможно. Выявляются они лишь при многократных
измерениях одной и той же величины и подчиняются определенным
закономерностям. Изучая эти закономерности, можно ослабить или
уменьшить их влияние, получить более надежный результат и
произвести оценку точности измерения.

9. Случайные погрешности. Их свойства

Случайные погрешности обладают следующими свойствами:
1.При определенных условиях измерений по своей
абсолютной величине не превышают определенного
предела:
пред
2. Малые по абсолютной величине погрешности встречаются
чаще, чем большие.
3. При неограниченном увеличении числа измерений
количество погрешностей со знаком "+" приближается к
количеству погрешностей со знаком "-".

10.

4. Среднее арифметическое из числа случайных погрешностей
при неограниченном возрастании количества измерений
стремится к нулю.
1 2 3 ... n
lim
0
lim
n
n
n
n
Эта формула выражает свойство компенсации случайных
ошибок.
Это свойство относится и к сумме попарных произведений
случайных погрешностей.
lim
n
. 0
i
j
n
где Δi и Δj - любые две погрешности из ряда измерений одной и
той же величины.
Отклонение среднего арифметического от нуля
свидетельствует о наличии в результах измерений
систематических погрешностей.

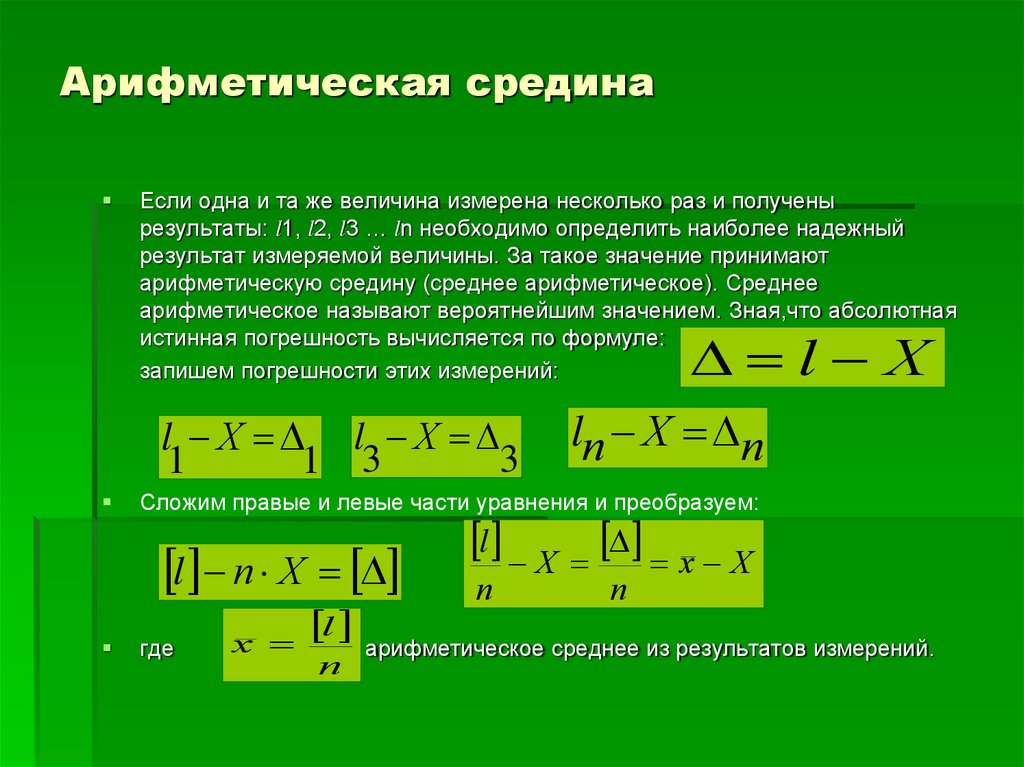
11. Арифметическая средина

Если одна и та же величина измерена несколько раз и получены
результаты: l1, l2, l3 … ln необходимо определить наиболее надежный
результат измеряемой величины. За такое значение принимают
арифметическую средину (среднее арифметическое). Среднее
арифметическое называют вероятнейшим значением. Зная,что абсолютная
истинная погрешность вычисляется по формуле:
запишем погрешности этих измерений:
l Х
l Х l Х
3
1
1 3
Сложим правые и левые части уравнения и преобразуем:
l п Х
lп Х п
где
х
l
п
l Х х Х
п
п
- арифметическое среднее из результатов измерений.

12. При неограниченном возрастании числа измерений n:

п
п
Следовательно, с увеличением числа
измерений арифметическое среднее
стремится к истинному значению х X
Поэтому принято считать, что
арифметическое среднее является наиболее
надежным значением измеренной величины
при всяком количестве измерений.

13. Средняя квадратическая погрешность одного измерения

Имея ряд геодезических измерений одной и той же
величины, мы должны уметь оценивать точность
как одного измерения, так и арифметической
средины.
...
l1 Х 1 , l2 Х 2 ,l3 Х 3 …lп Х п
В этом ряде:
l - измеренные значения;
X - истинное значение;
Δ - абсолютная истинная погрешность каждого измерения;
n - число измерений.

14. С какой средней погрешностью выполнено одно измерение, любое из этого ряда. Например, ряд такой: 5; 6; 8; 9; 10; +12; +13.

... n
2
3
1
n
n
Т.е. в данном ряде средняя ошибка измерения:
θ 9
Можно все погрешности записать в ряд в порядке
возрастания их величин и определить среднюю
цифру ряда и принять ее за вероятную погрешность
любого одного измерения этого ряда, таким образом
находится вероятная погрешность: “r”.
5;6;8;9;10; 12;13.

15.

Карл Фридрих Гаусс (1777-1855 гг.) - немецкий
математик и астроном предложил погрешность
одного измерения определять по средней
квадратичной погрешности. Суть его предложения
состоит в том, что каждая погрешность ряда
возводится в квадрат, затем складываются все
погрешности, полученная сумма делится на число
измерений и извлекается квадратный корень.
Полученную погрешность одного измерения Гаусс
назвал средней квадратической погрешностью (СКП).
Она обозначается т:
21 22 23 ... 2п
m
п
В примере:
m
2
п
24
1,5
10
СКП строже оценивает результат измерения и в этом
ее преимущество над Θ и r.

16. Относительные и предельные погрешности

Из исследований установлено, что при
достаточно большом числе измерений,
случайные погрешности:
в 30-32 случаях из 100 превосходят т;
в 5 случаях из 100 превосходят 2 т;
в 3 случаях из 1000 превосходят 3 т.

17. В качестве предельной погрешности (предельно-допустимой невязки, предельного допуска) принимают утроенную среднюю

квадратическую
ошибку:
пред f доп 3m
Для повышения требований к точности
измерений при определенных условиях
измерений часто предельную погрешность
принимают:
пред 2m

18. Относительные погрешности

Оценку точности линейных измерений производят
по относительной погрешности: отношение
абсолютной погрешности к измеряемой величине.
Относительная погрешность выражается
обыкновенной дробью, в числителе которой I, а в
знаменателе - число, показывающее на какую
величину измерения допускается погрешность в
единицу данной меры.
1 1
l
l
N l

19. Средняя квадратическая погрешность функций измеренных величин

Нередко
определяемая
величина
является
функцией других непосредственно измеряемых
величин, поэтому возникает вопрос о вычислении
СКО функции измеренных величин.
Рассмотрим функцию вида:
u k x
x - измеренное значение величины с погрешностью ∆x
k - безошибочный постоянный сомножитель;
u - вычисленное значение функции с погрешностью ∆u

20. Если x изменить на ∆x , то u изменится на ∆u. Получаем:

u u k х х
где ∆x и ∆u - случайные погрешности аргумента x
и функции u.
Сопоставляя это уравнение с исходным
выражением, запишем:
u k х

21. Если величина x измерялась “n” раз, то таких уравнений будет:

u1 k х1
u 2 k х2
u3 k х3
…
u п k х п

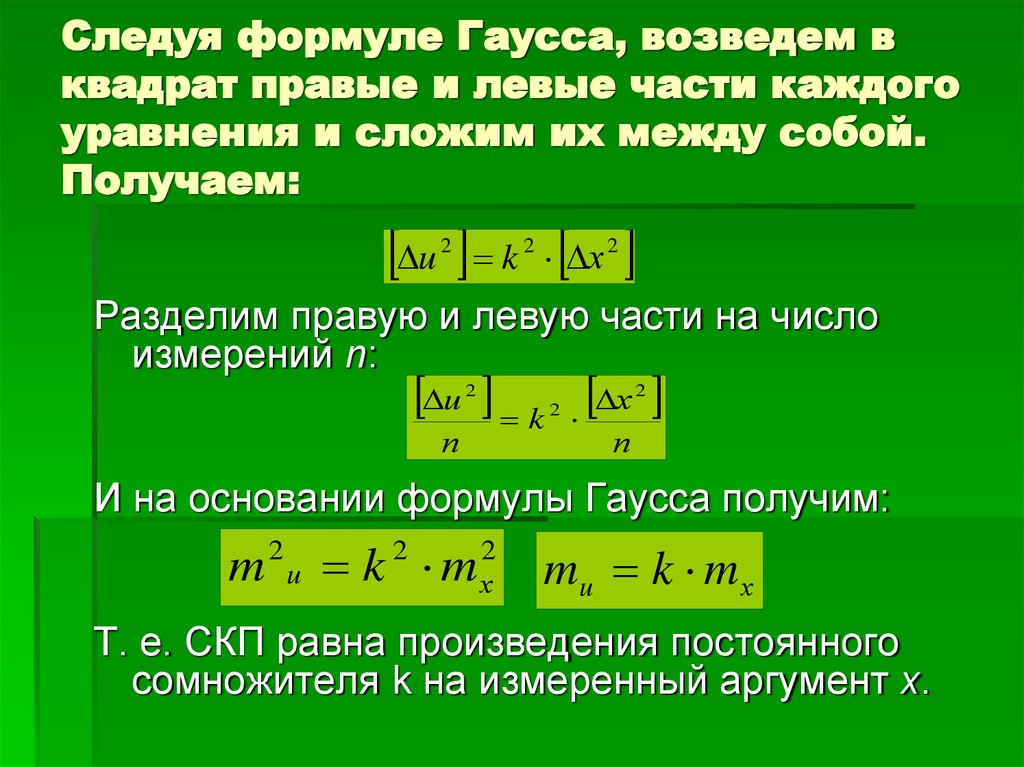
22. Следуя формуле Гаусса, возведем в квадрат правые и левые части каждого уравнения и сложим их между собой. Получаем:

u k х
2
2
2
Разделим правую и левую части на число
измерений n:
u k х
2
2
2
п
п
И на основании формулы Гаусса получим:
m u k m
2
2
2
х
mu k m х
Т. е. СКП равна произведения постоянного
сомножителя k на измеренный аргумент x.

23. Средняя квадратическая погрешность функции

Линейная функция алгебраической суммы:
u x у
где x и y - независимые, непосредственно
измеренные величины;
u - функционально зависимая от x и y
вычисляемая величина (косвенное измерение).
С учетом погрешностей:
u и x х у у
где Δu - погрешность алгебраической суммы.

24.

Сопоставляя с исходным, получаем:
при многократном измерении величин Х и У:
u1 x1 у1
u2 x2 у2
u3 x3…
у3
u п xп уп

25. Возведем левые и правые части в квадрат, сложим все уравнения и разделим на число, получим:

u х у 2 х у
2
п
2
п
2
п
п
На основании четвертого свойства случайных
погрешностей:
i . j
lim
n
n
0
На основании формулы Гаусса: m 2 u тх2 т у2
Рассуждая аналогично, можно доказать, что
погрешность алгебраической разности выразится
точно так же: u x у
m2u т2 т2
х
у