Similar presentations:
Исследование корней квадратного трехчлена
1.
10 классИсследование
корней
квадратного
трехчлена
2.
Ряд задач, предлагаемых выпускникам11класса на итоговой аттестации в форме
ЕГЭ, требуют знаний, умений, навыков в
исследовании расположения корней
квадратного трёхчлена a x² + b x + c
относительно других чисел числовой
прямой.
ДЕМО 2008. Найти все значения a, для
которых при каждом х из промежутка (-3; -1]
значение выражения х4 − 8х2 − 2 ≠ а х2
3.
Примеры задач решаемые с опорой натеоремы о корнях квадратного трёхчлена
№1. При каких значениях параметра а корни
уравнения ax ² − 2(a + 4)x −1=0 имеют
одинаковые знаки.
№ 2. При каких значениях параметра а
уравнение x² −2ax + a² −a−6=0 имеет два
разных отрицательных корня?
№3. При каких значениях параметра k
оба корня уравнения x² +4kx+ (1 − 2k + 4k²)=0
действительны и меньше, чем − 1.
4.
Т.1. Для того, чтобы корни квадратноготрехчлена a x² + b x + c были действительны
и имели одинаковые знаки, необходимо и
достаточно, чтобы:
D ≥ 0,
при этом:
если
если
5.
Т.2. Для того, чтобы корни трехчленаa x² + b x + c были действительны и имели
разные знаки, необходимо и достаточно,
чтобы:
D ≥ 0,
6.
Т.3. Если оба корня больше некоторогозаданного числа А ,
х
то
(Здесь и далее
)
7.
Т.4. Если оба корня меньше некоторогозаданного числа В,
х
то
8.
Т.5. Если оба корня принадлежат заданномупромежутку (A; B),
х
то
9.
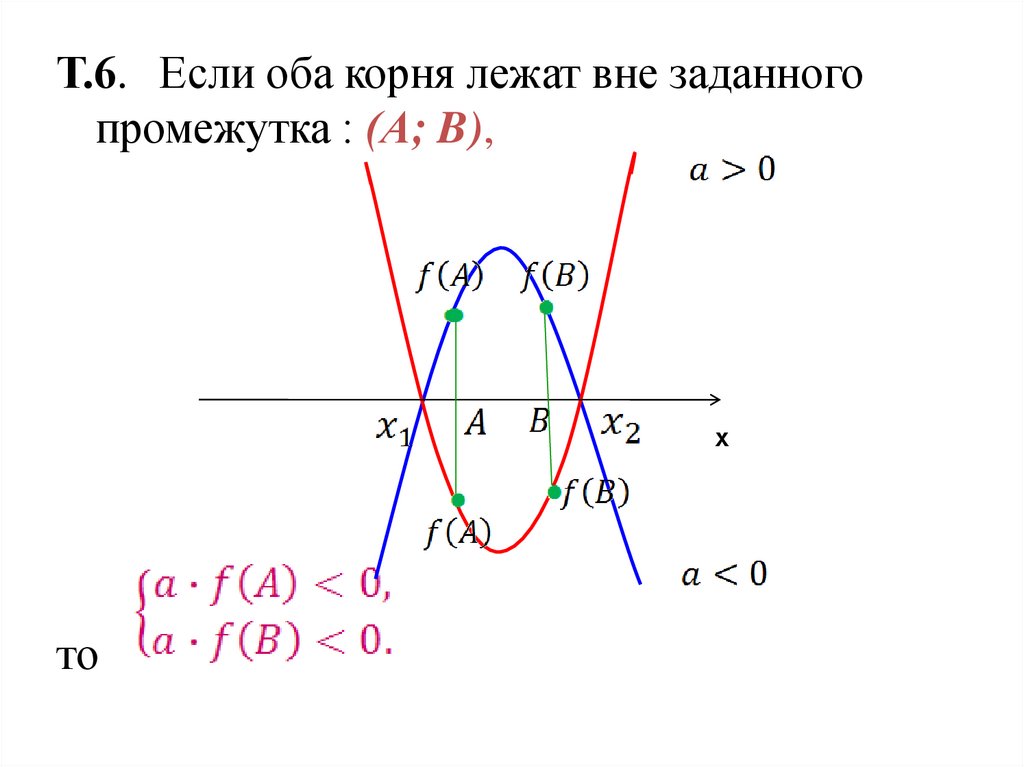
Т.6. Если оба корня лежат вне заданногопромежутка : (А; B),
х
то
10.
Т.7. Если заданное число А лежит междукорнями,
х
то
11.
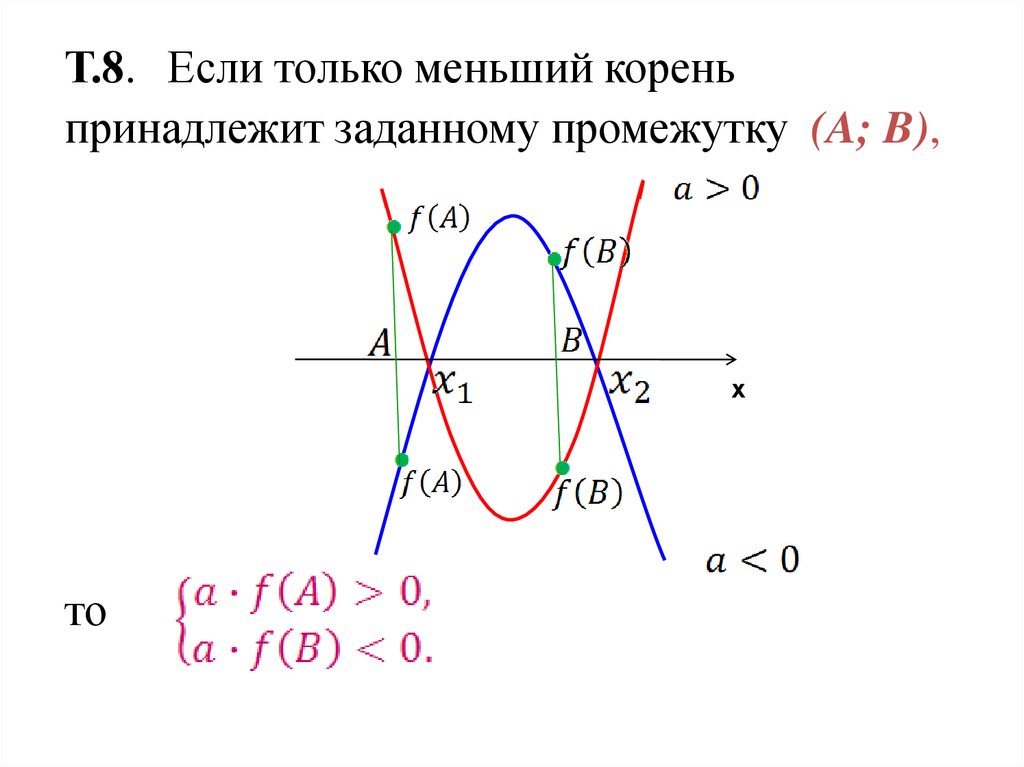
Т.8. Если только меньший кореньпринадлежит заданному промежутку (A; B),
х
то
12.
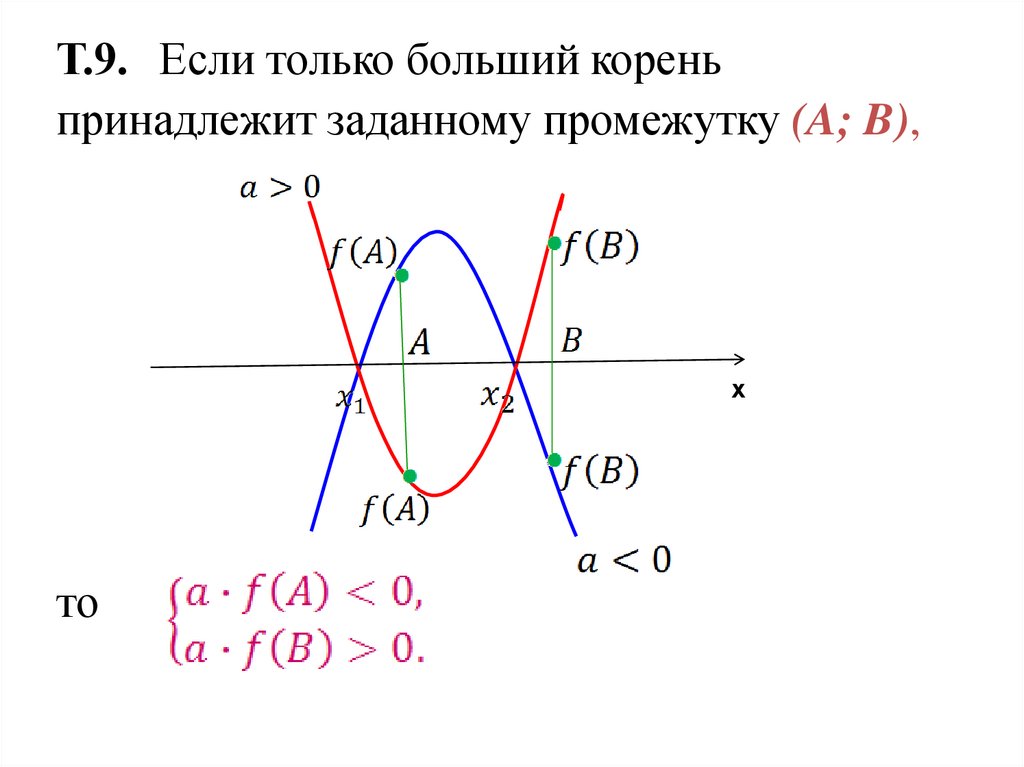
Т.9. Если только больший кореньпринадлежит заданному промежутку (A; B),
х
то









 mathematics
mathematics








