Описанный многоугольник

1. 19 апреля Классная работа

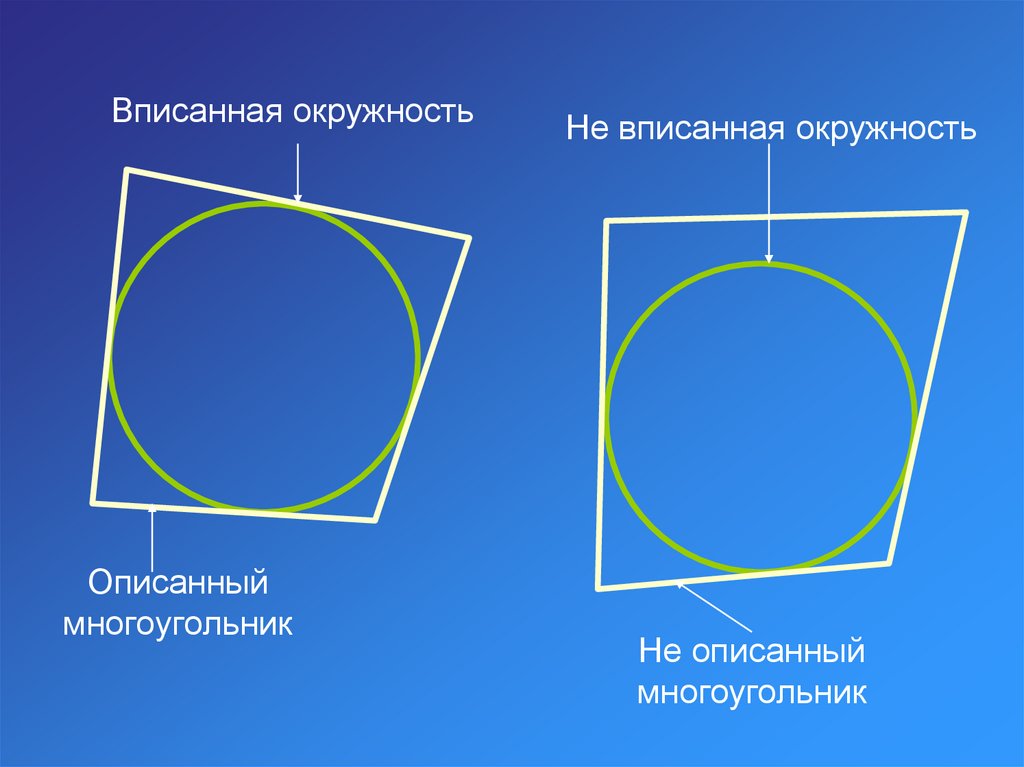
Вписанная
окружность

2.

Вписанная окружность
Описанный
многоугольник
Не вписанная окружность
Не описанный
многоугольник

3.

Опр.: Окружность называется вписанной
в многоугольник, если все стороны
многоугольника касаются окружности,
а многоугольник называется
описанным около этой окружности.

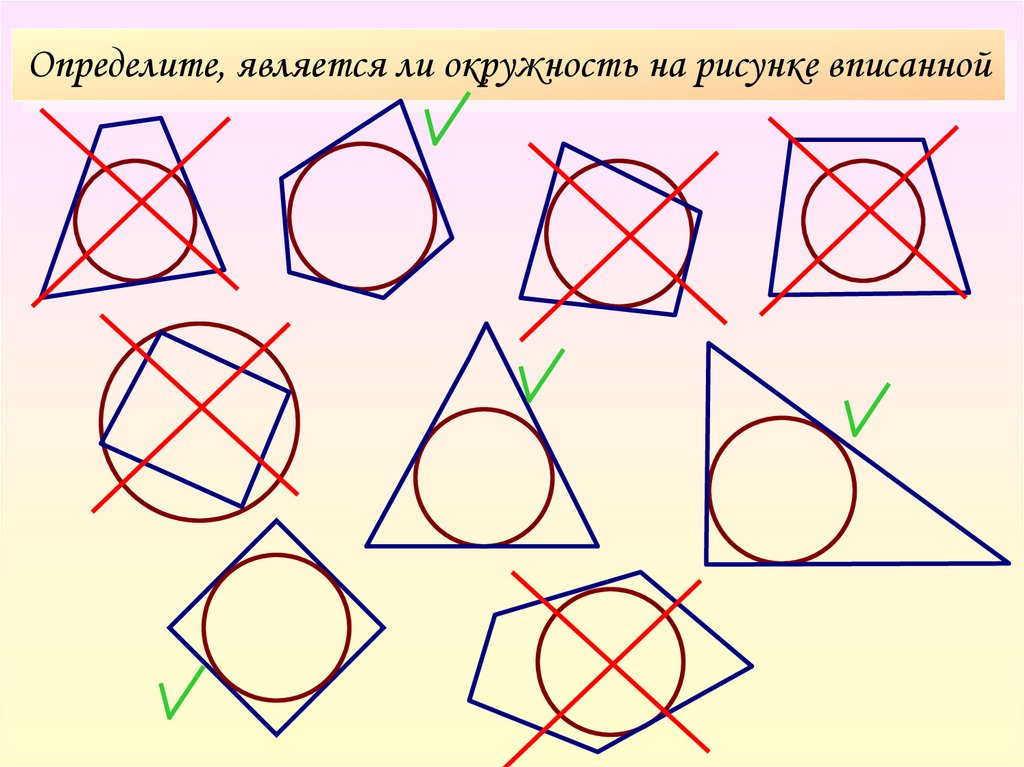
4. Определите, является ли окружность на рисунке вписанной

5. Задание: Постройте в тетради описанные около окружностей треугольник и четырёхугольник.

6. Теорема: В любой треугольник можно вписать окружность.

Вопрос: в любой ли треугольник можно
вписать окружность?
Задание: 3 человека у доски строят
треугольники разных видов и
пытаются вписать окружность.
Теорема: В
любой
треугольник можно
вписать окружность.

7. Вопрос 1: Сколько окружностей можно вписать в треугольник?

Ответ: В треугольник можно вписать
только одну окружность?
Вопрос 2: Во всякий ли
четырёхугольник можно вписать
окружность?
Ответ: Не во всякий четырёхугольник
можно вписать окружность.

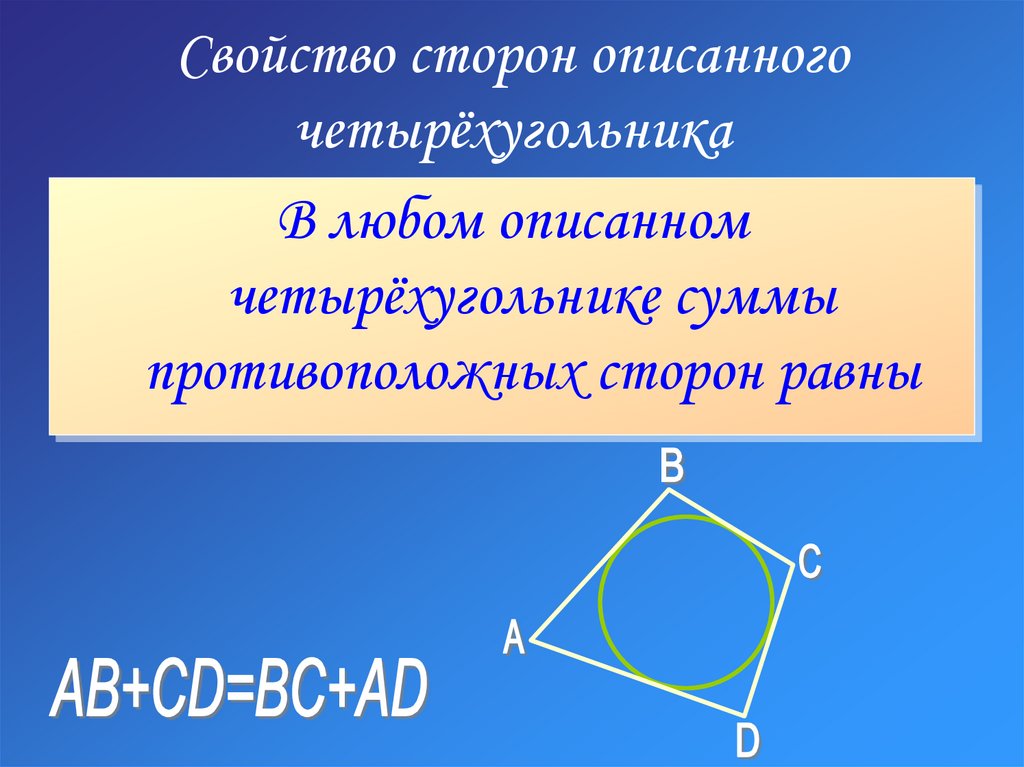
8. Свойство сторон описанного четырёхугольника

В любом описанном
четырёхугольнике суммы
противоположных сторон равны

9. Сформулируйте обратное свойство:

Если суммы противоположных
сторон выпуклого
четырёхугольника равны, то в
него можно вписать окружность.

10. Выполните упражнения:

691
692
Домашнее задание:
693 + учить
теорию