Вписанные и описанные четырехугольники

1. Вписанные и описанные четырехугольники

2.

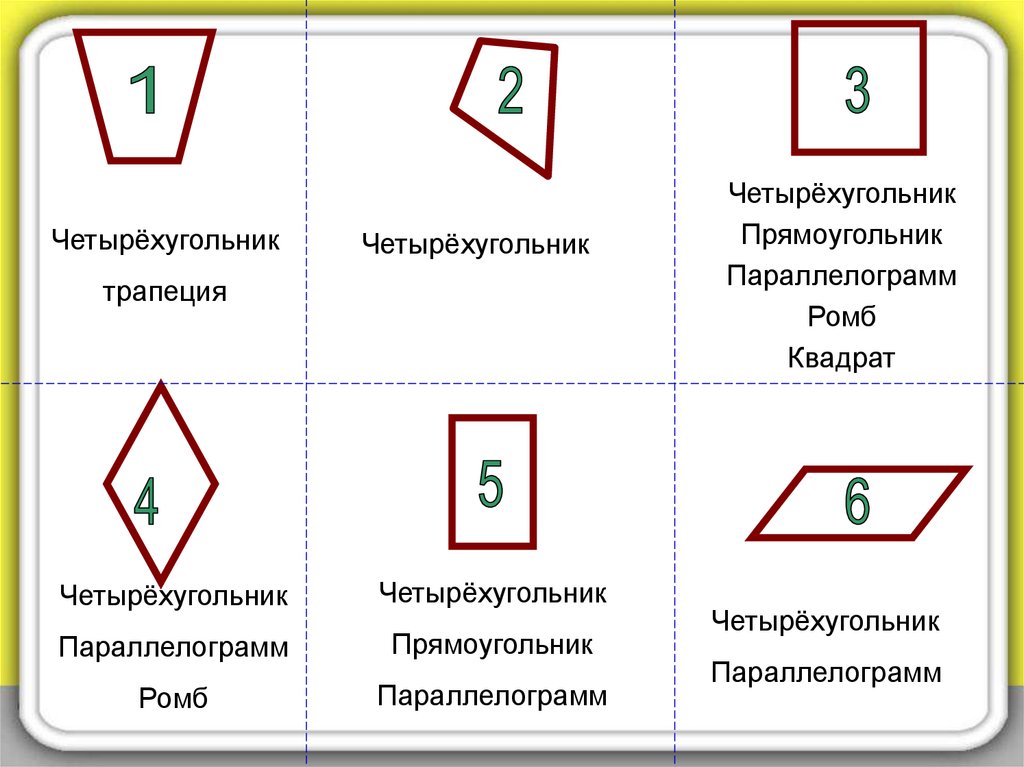
Четырёхугольник
Четырёхугольник
трапеция
Четырёхугольник
Четырёхугольник
Параллелограмм
Прямоугольник
Ромб
Параллелограмм
Четырёхугольник
Прямоугольник
Параллелограмм
Ромб
Квадрат
Четырёхугольник
Параллелограмм

3.

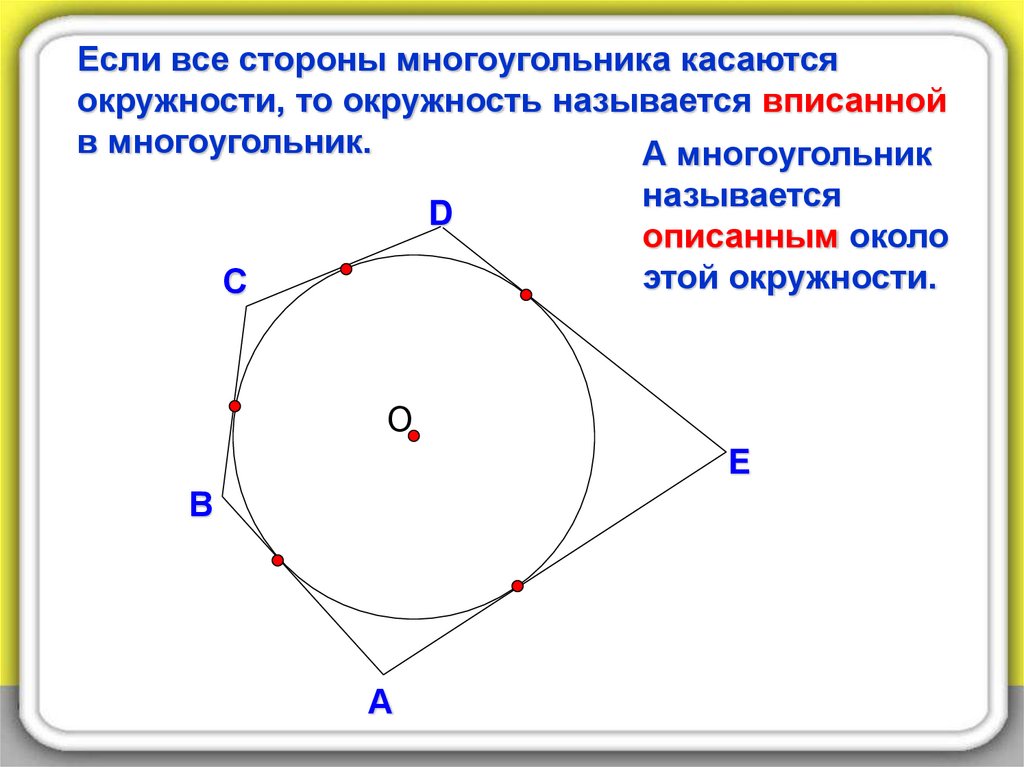
Если все стороны многоугольника касаются
окружности, то окружность называется вписанной
в многоугольник.
А многоугольник
D
С
называется
описанным около
этой окружности.
О
E
В
А

4.

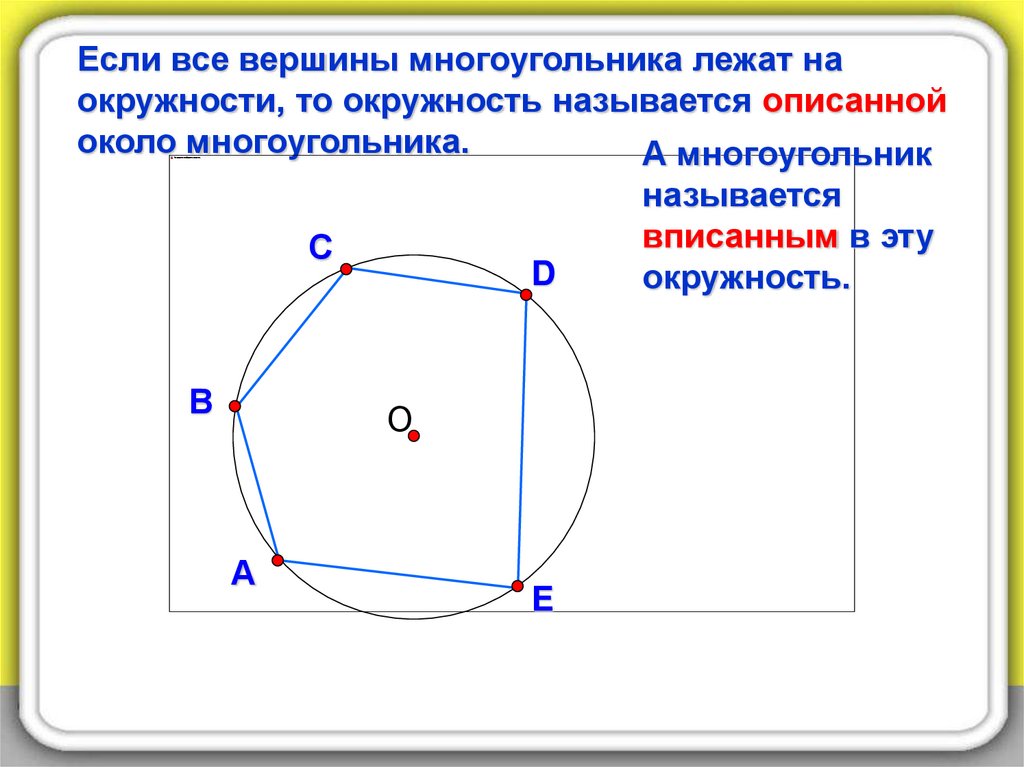
Если все вершины многоугольника лежат на
окружности, то окружность называется описанной
около многоугольника.
А многоугольник
С
В
D
О
А
E
называется
вписанным в эту
окружность.

5.

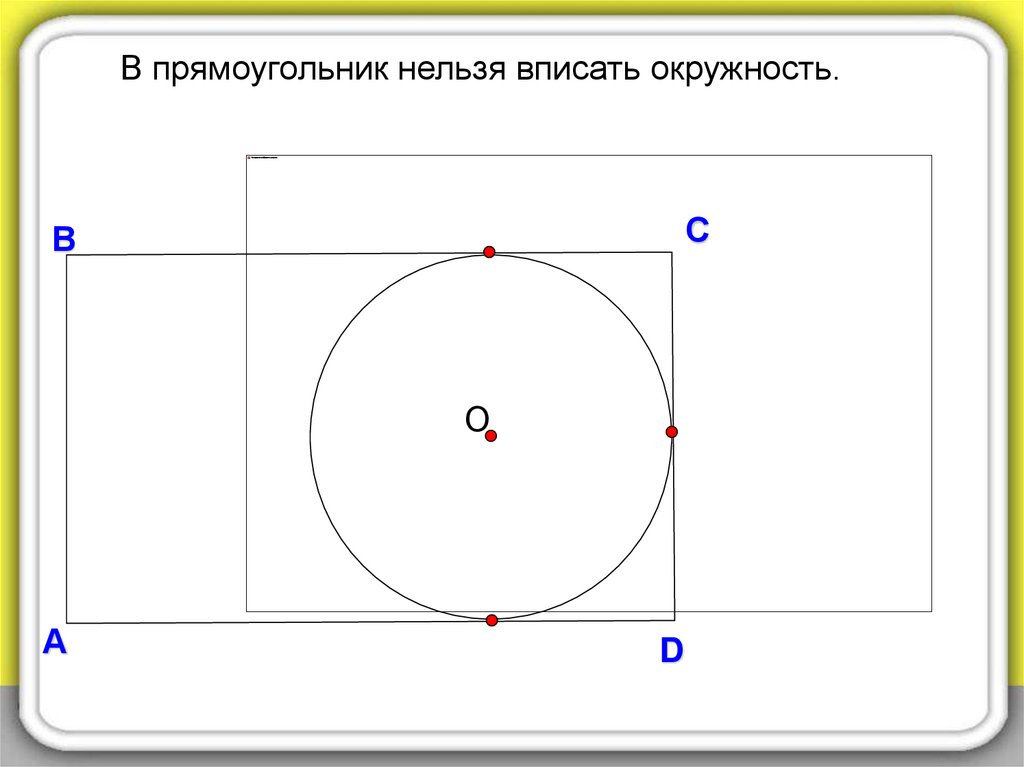
В прямоугольник нельзя вписать окружность.
С
В
О
А
D

6.

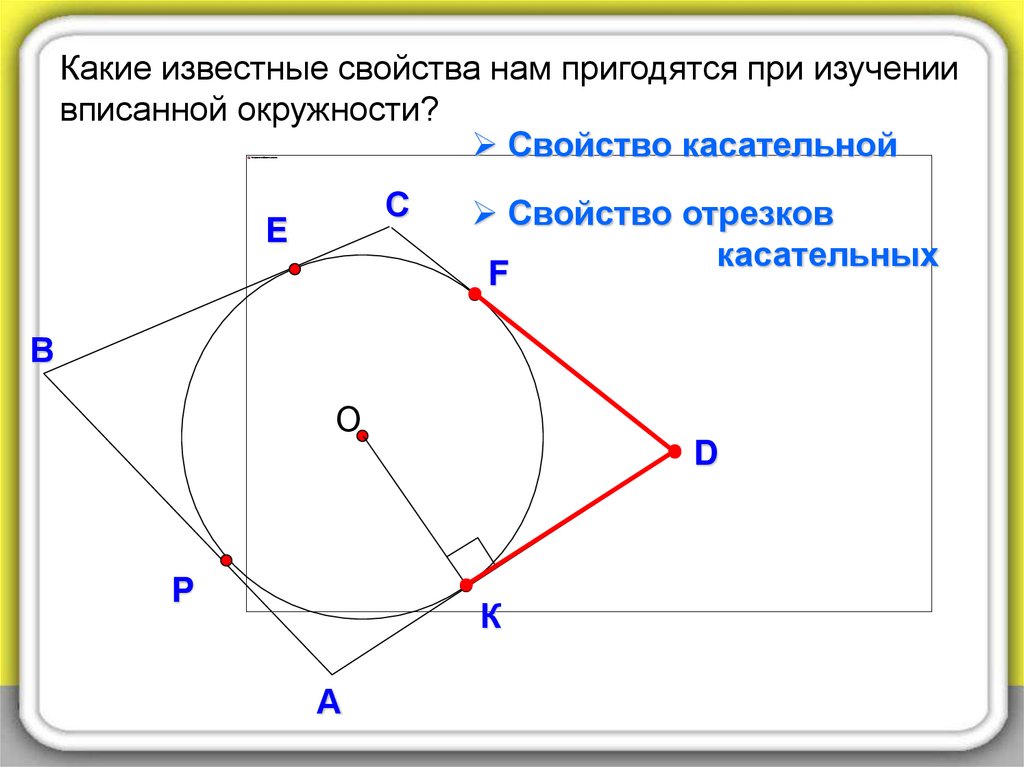
Какие известные свойства нам пригодятся при изучении
вписанной окружности?
Свойство касательной
С
E
Свойство отрезков
касательных
F
В
О
D
P
К
А

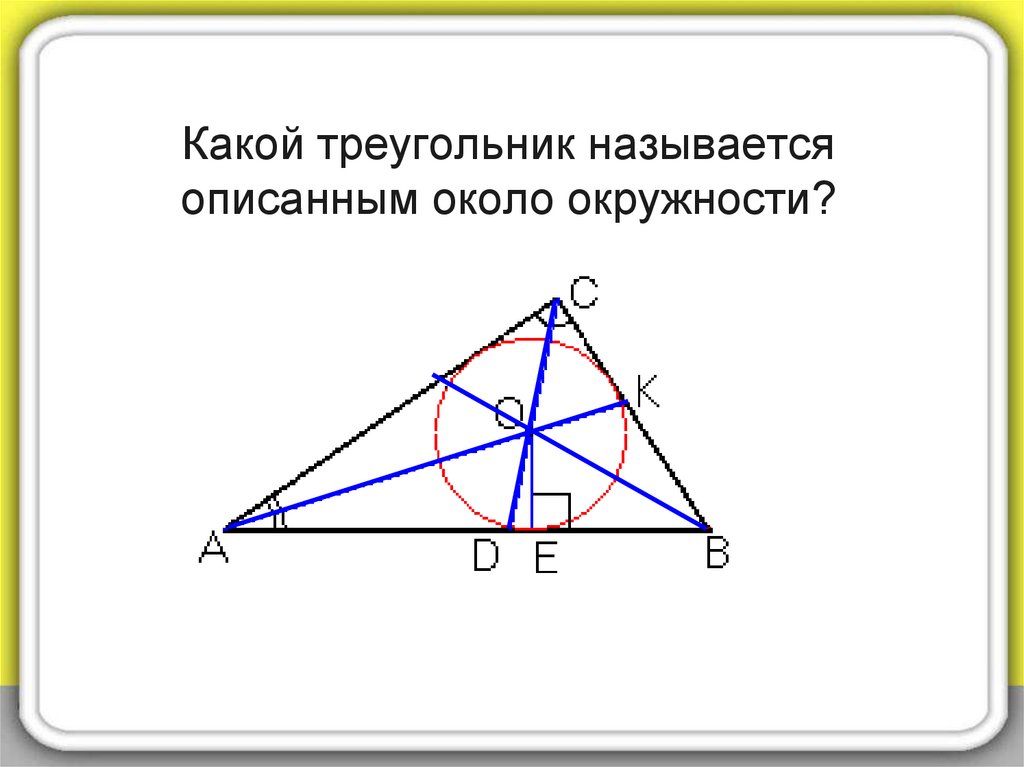
7. Какой треугольник называется описанным около окружности?

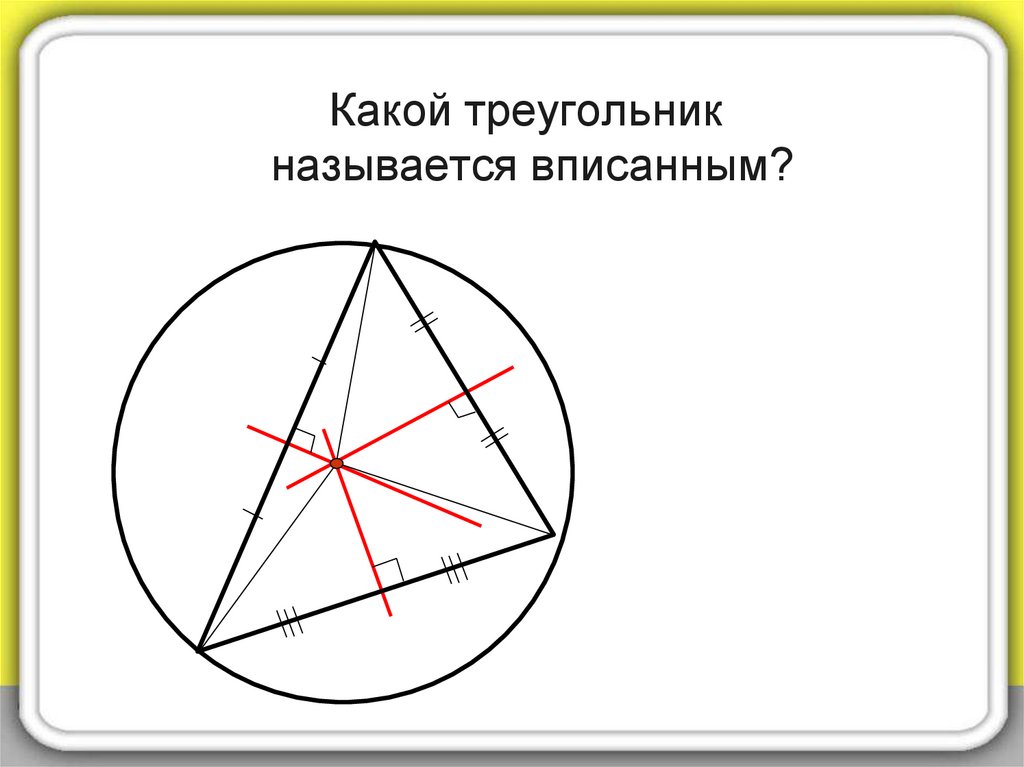
8. Какой треугольник называется вписанным?

9.

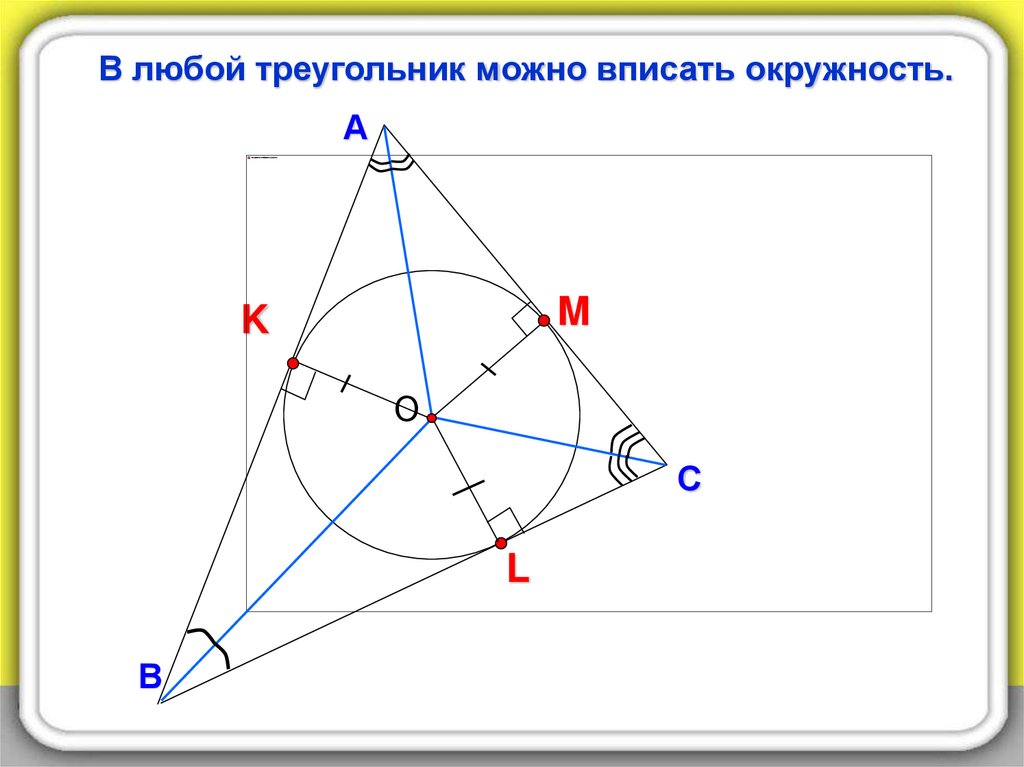
В любой треугольник можно вписать окружность.
А
M
K
О
С
L
В

10.

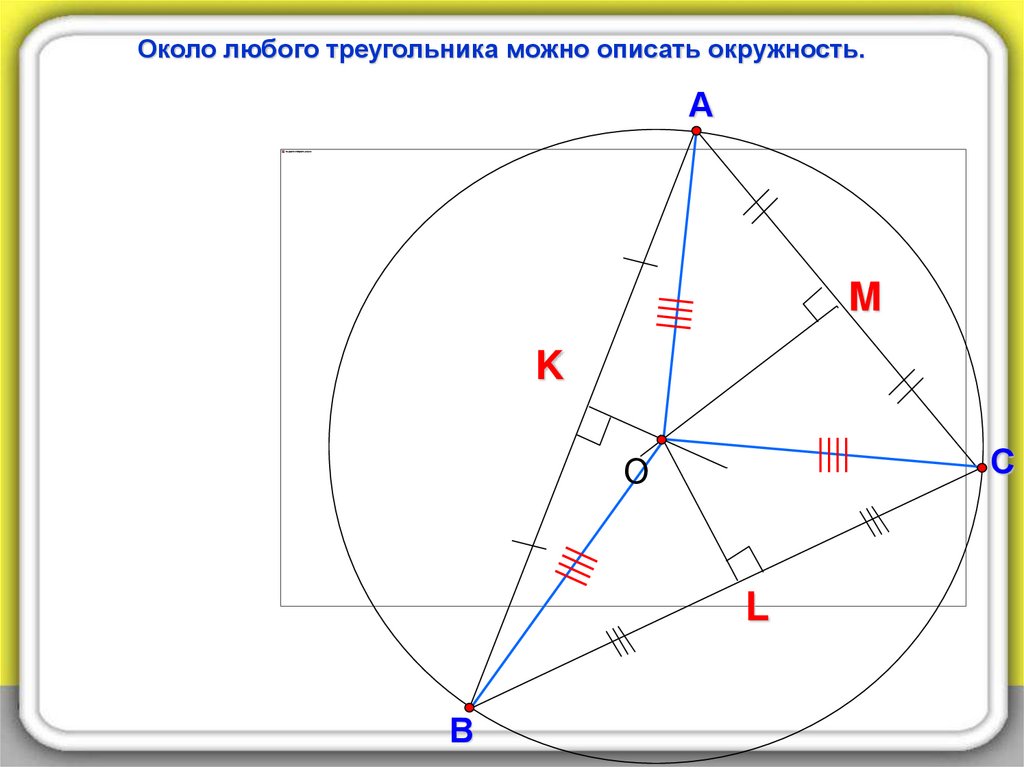
Около любого треугольника можно описать окружность.
А
M
K
С
О
L
В

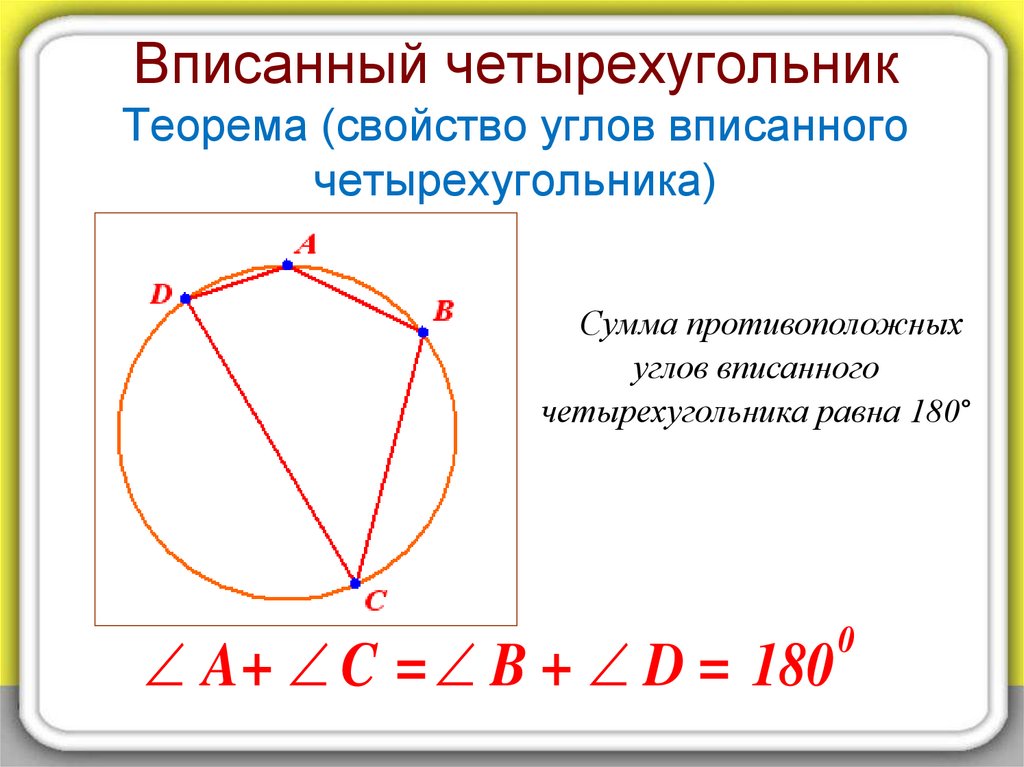
11. Вписанный четырехугольник Теорема (свойство углов вписанного четырехугольника)

Сумма противоположных
углов вписанного
четырехугольника равна 180°
A+ C = B + D = 180
0

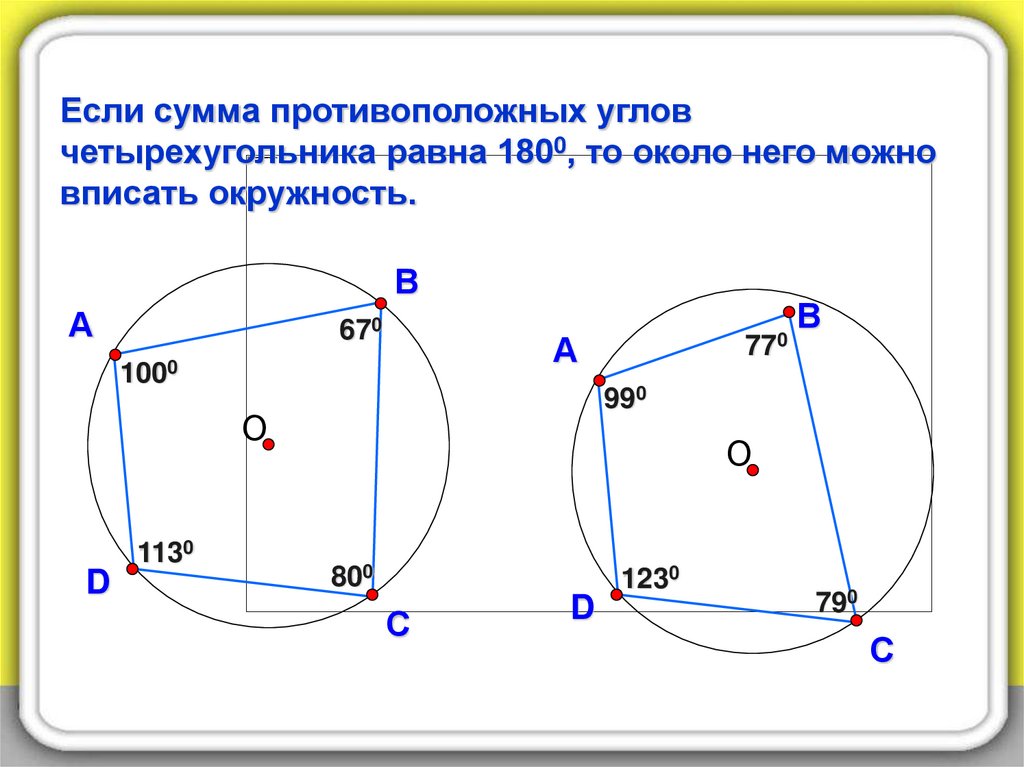
12.

Если сумма противоположных углов
четырехугольника равна 1800, то около него можно
вписать окружность.
В
А
670
А
1000
D
В
990
О
1130
770
О
800
1230
С
D
790
С

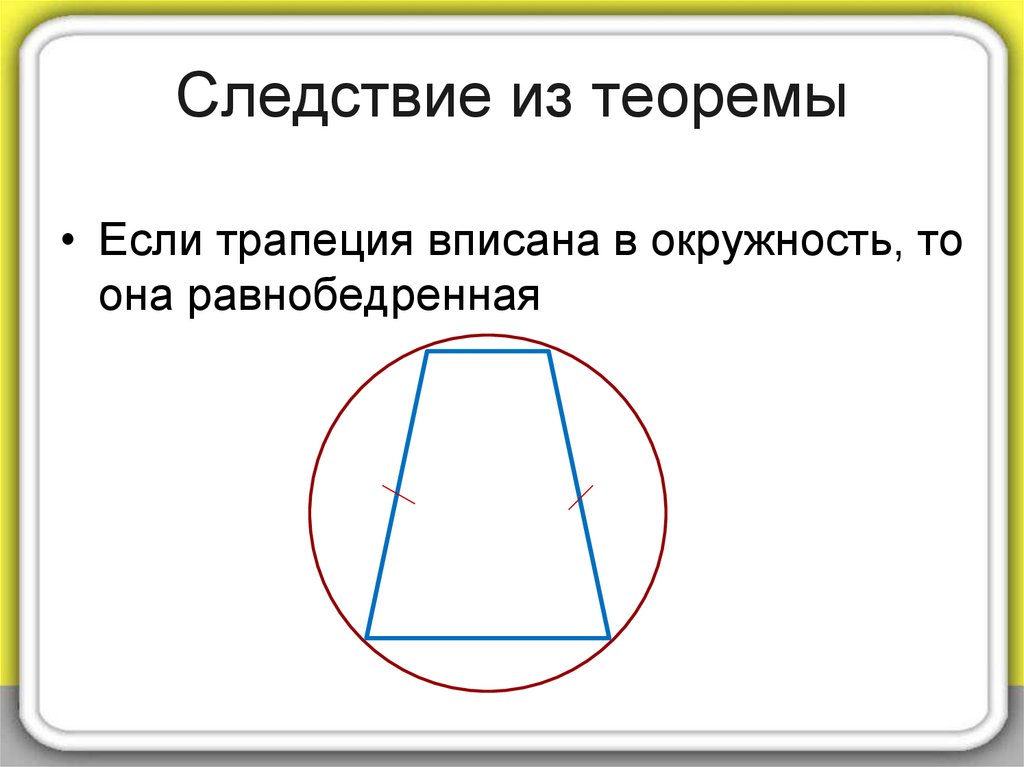
13. Следствие из теоремы

• Если трапеция вписана в окружность, то
она равнобедренная

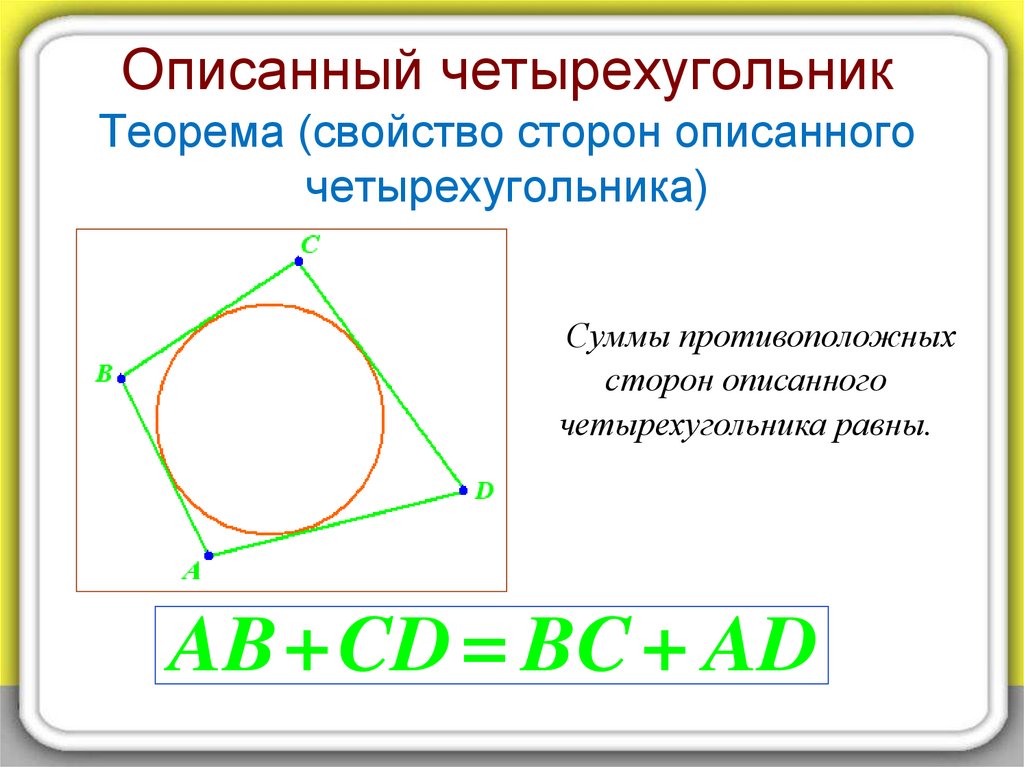
14. Описанный четырехугольник Теорема (свойство сторон описанного четырехугольника)

Суммы противоположных
сторон описанного
четырехугольника равны.
AB+CD = BC + AD

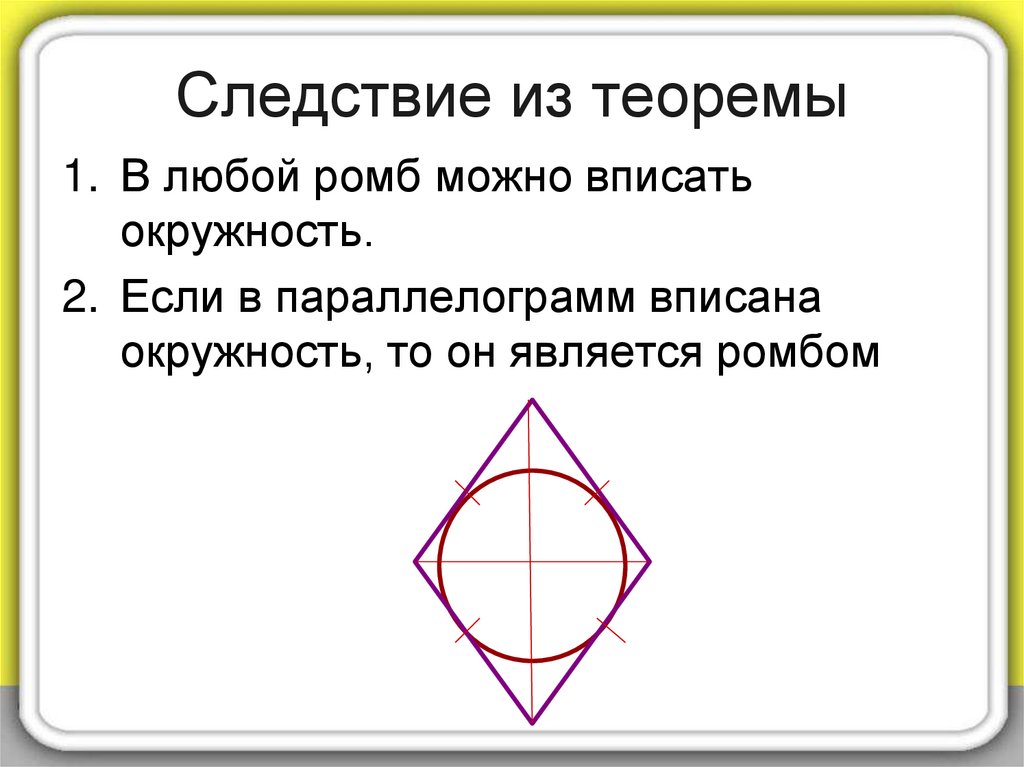
15. Следствие из теоремы

1. В любой ромб можно вписать
окружность.
2. Если в параллелограмм вписана
окружность, то он является ромбом