Similar presentations:
Вписанная и описанная окружности
1.
2.
Вписанная и описанная окружностьОкружность называется вписанной в
многоугольник,
если все стороны многоугольника
касаются этой окружности.
Окружность называется описанной
около многоугольника, если все его
вершины лежат на этой
окружности.
3.
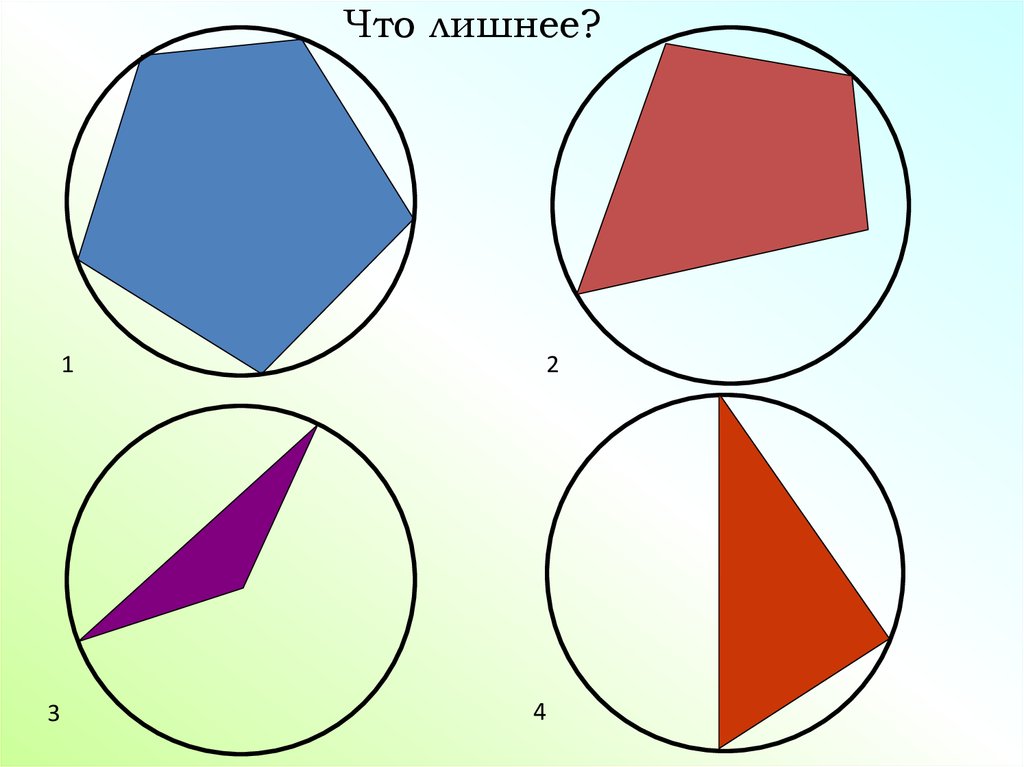
Что лишнее?1
3
2
4
4.
Что лишнее?1
2
3
4
5. Теорема об окружности, вписанной в треугольник.
В любой треугольник можно вписатьокружность и притом только одну.
Центр вписанной
окружности является
точкой пересечения
биссектрис
треугольника.
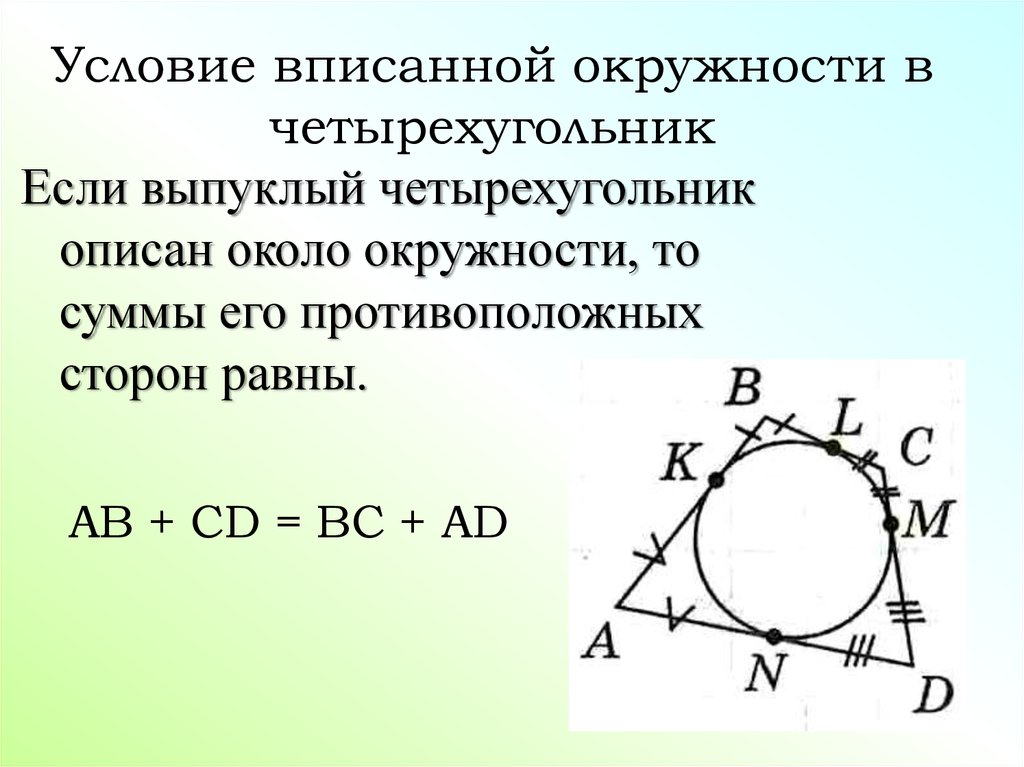
6. Условие вписанной окружности в четырехугольник
Если выпуклый четырехугольникописан около окружности, то
суммы его противоположных
сторон равны.
AB + CD = BC + AD
7. Положение центра окружности, вписанной в четырехугольник
Если существует окружность, вписанная вчетырехугольник, то она единственная, и ее
центр лежит на пересечении биссектрис
углов этого четырехугольника.
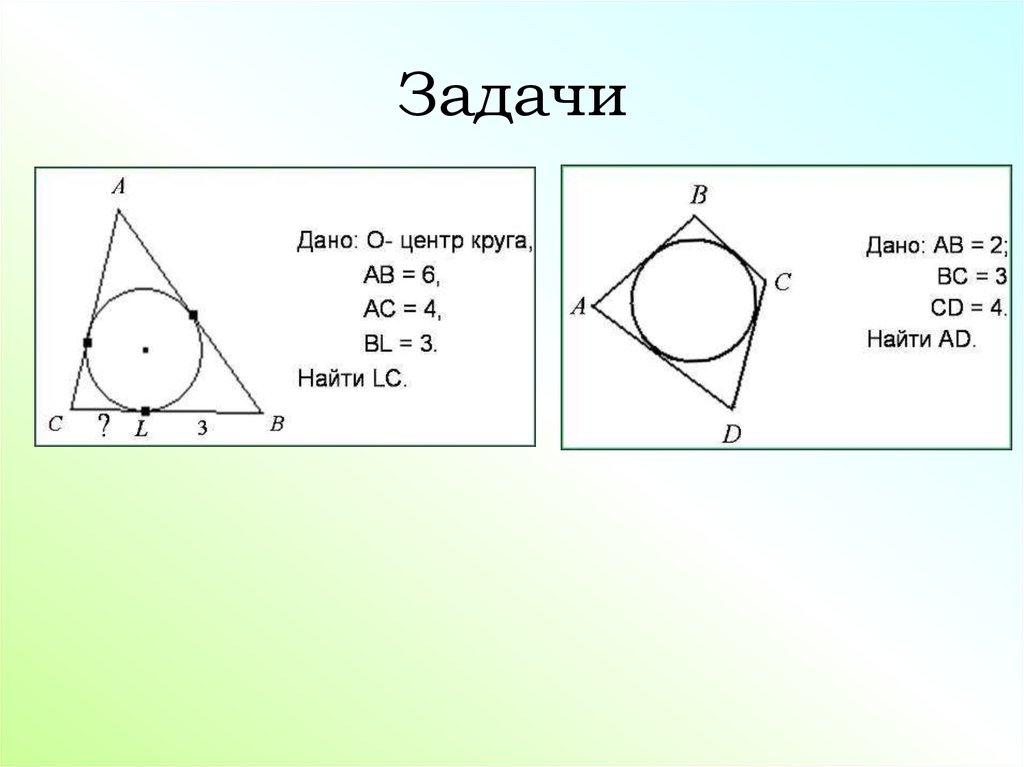
8. Задачи
9.
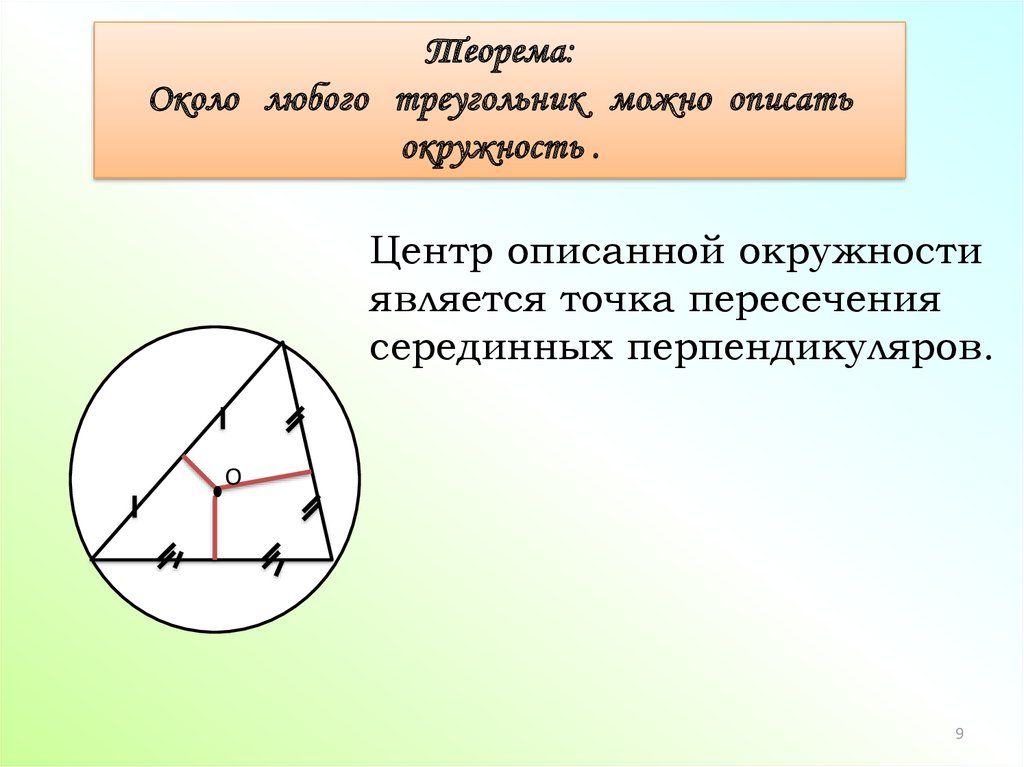
Теорема:Около любого треугольник можно описать
окружность .
Центр описанной окружности
является точка пересечения
серединных перпендикуляров.
О
9
10.
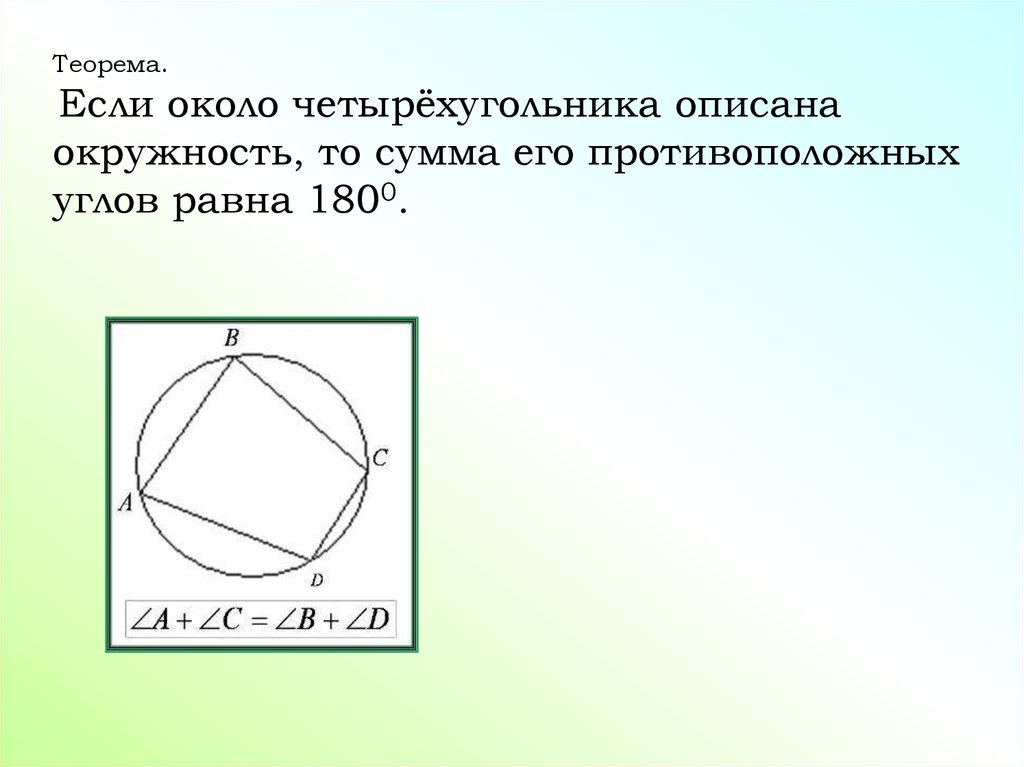
Теорема.Если около четырёхугольника описана
окружность, то сумма его противоположных
углов равна 1800.
11.
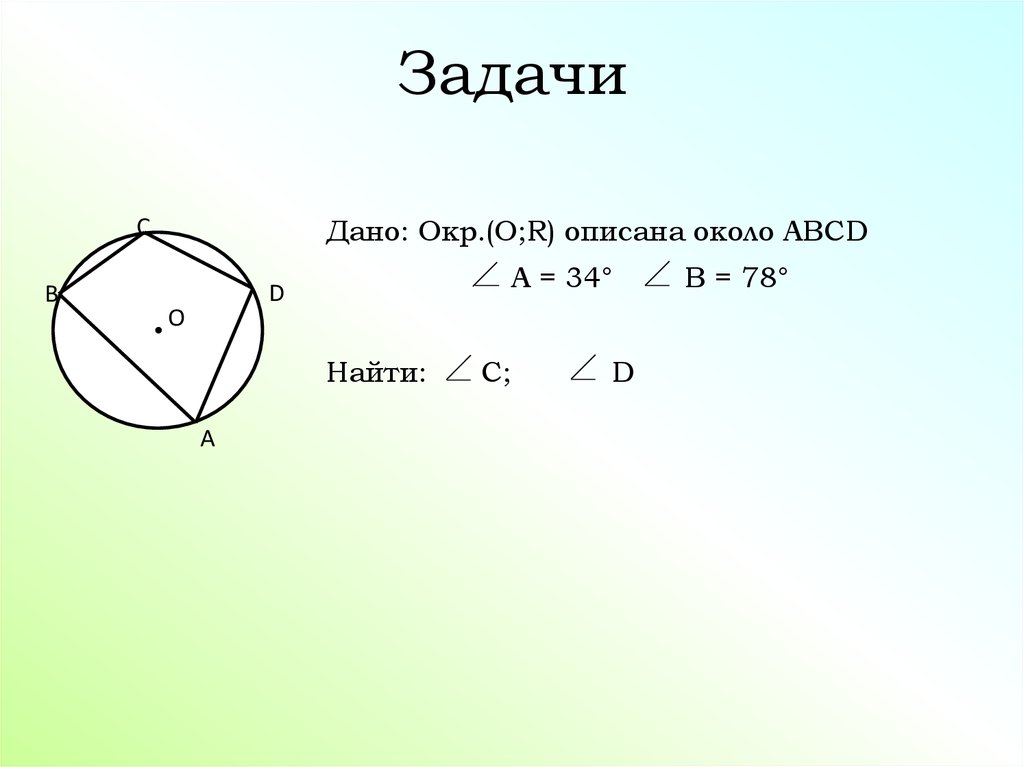
ЗадачиДано: Окр.(О;R) описана около АВСD
C
B
A = 34°
D
О
Найти:
A
С;
D
B = 78°
12.
Найти углы четырёхугольника РКЕН:Е
К
700
О
800
Р
Н
13.
Какой многоугольник называетсяправильным?
Правильным многоугольником называется
выпуклый многоугольник, у которого все
углы равны и все стороны равны.
14.
Вписанная и описанная окружностьОкружность, вписанная в правильный многоугольник,
касается сторон многоугольника в их серединах.








 mathematics
mathematics








