Какая окружность называется вписанной?

1. Повторим

• Какая окружность называется вписанной?
• В любой ли четырёхугольник можно вписать
окружность?
• Всегда ли вокруг окружности можно описать
треугольник?
• Любой ли треугольник может быть
описанным?
• Что является центром вписанной
окружности в треугольник?
• Назовите свойство описанного

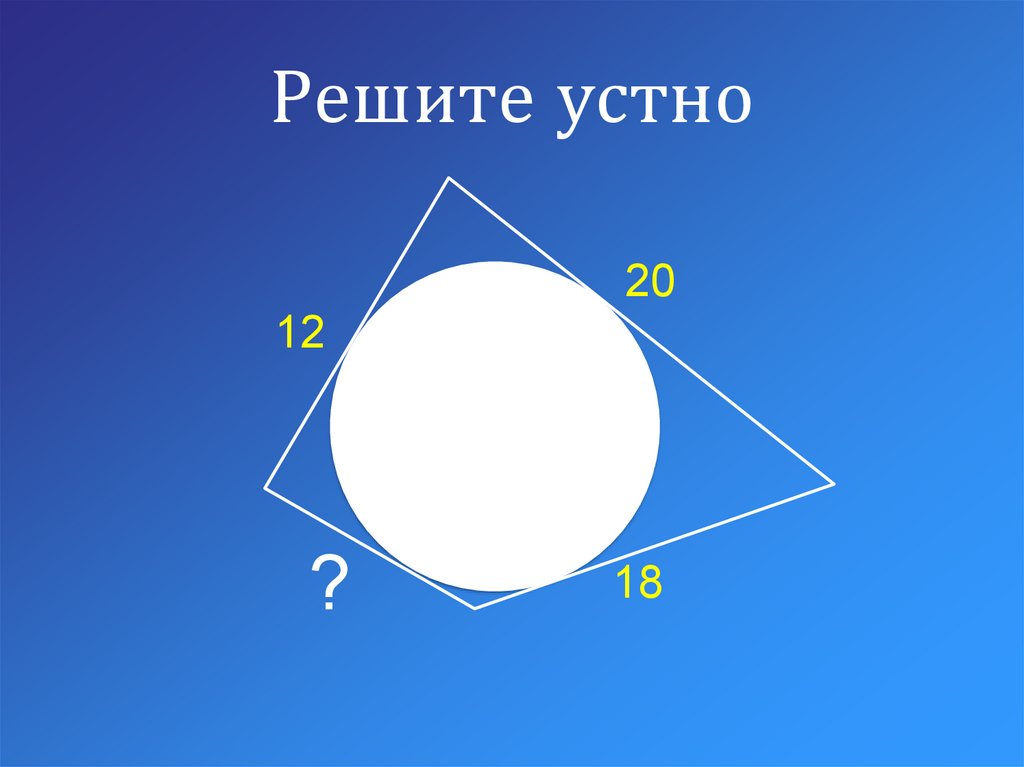
2. Решите устно

20
12
?
18

3. 16 апреля Классная работа

Описанная
окружность

4.

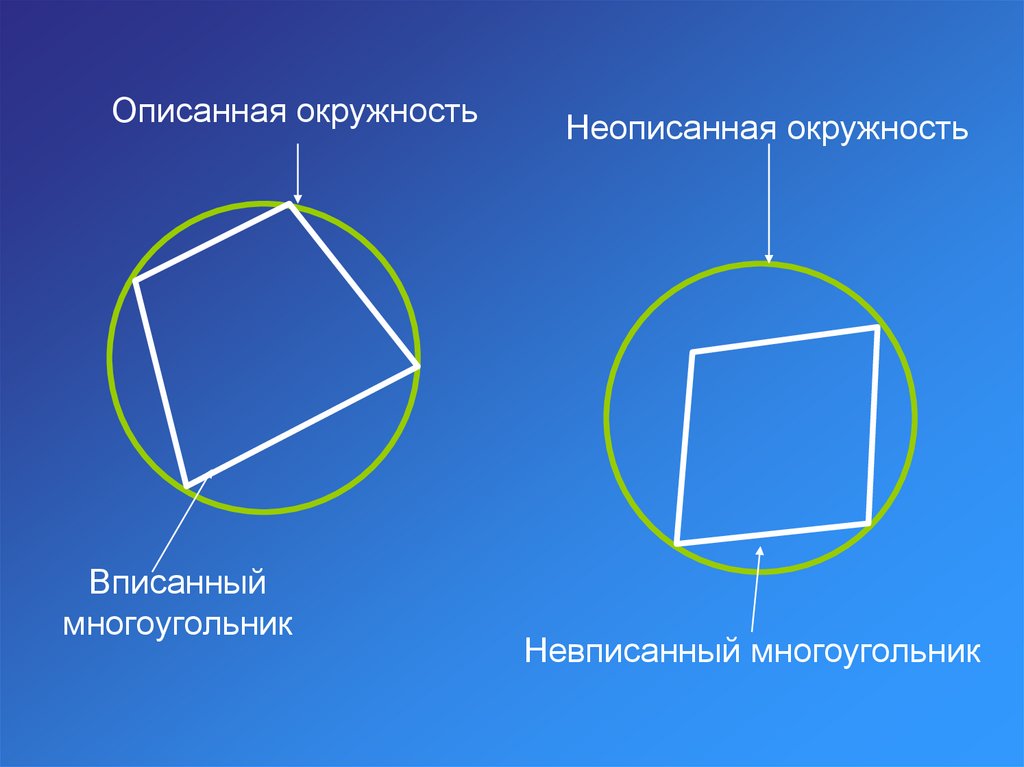
Описанная окружность
Вписанный
многоугольник
Неописанная окружность
Невписанный многоугольник

5.

Опр.: Окружность называется
описанной вокруг многоугольника,
если все вершины мн-ка лежат на
окружности. Мн-ник называется
вписанным в эту окружность.

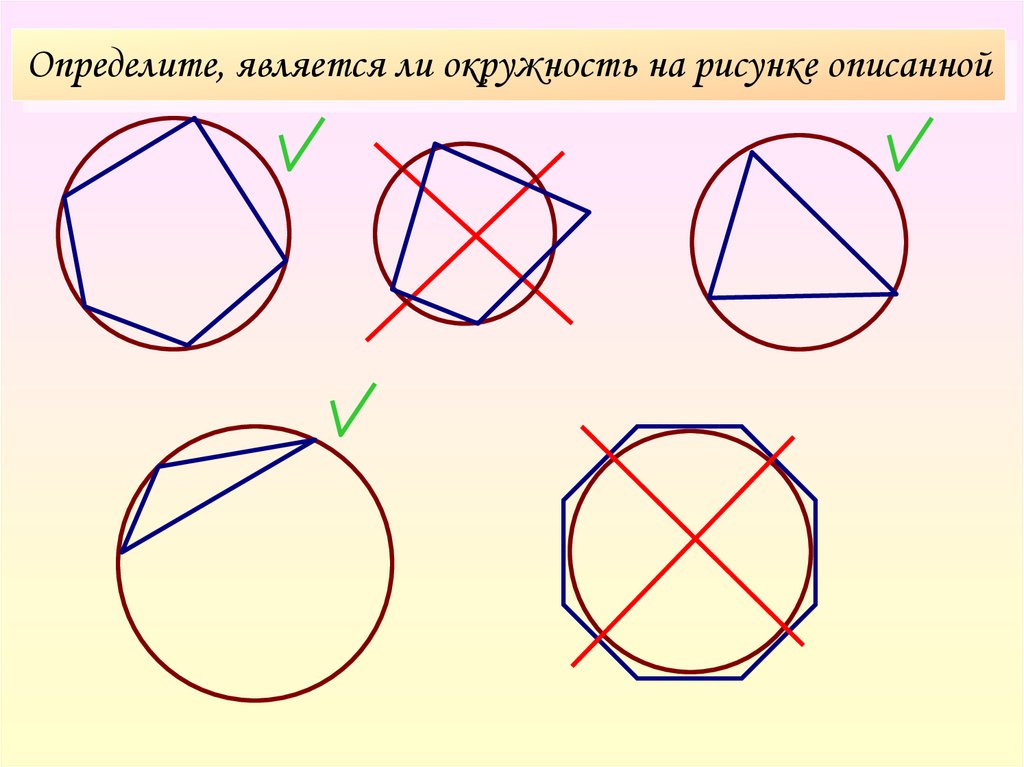
6. Определите, является ли окружность на рисунке описанной

7. Задание: Постройте в тетради вписанные в окружности треугольник и четырёхугольник.

8. Теорема: Около любого треугольника можно описать окружность. (центр описанной окружности – точка пересечения сер-х перп-ов)

Всегда ли около тр-ка можно описать окружность?
Что является центром описанной окружности?
Теорема: Около
любого
треугольника можно описать
окружность.
(центр описанной окружности – точка
пересечения сер-х перп-ов)

9. Вопрос 1: Сколько окружностей можно описать вокруг треугольника?

Ответ: Около треугольника можно
описать только одну окружность.
Вопрос 2: Около всякого ли
четырёхугольник а можно описать
окружность?
Ответ: Около четырёхугольника не
всегда можно описать окружность.

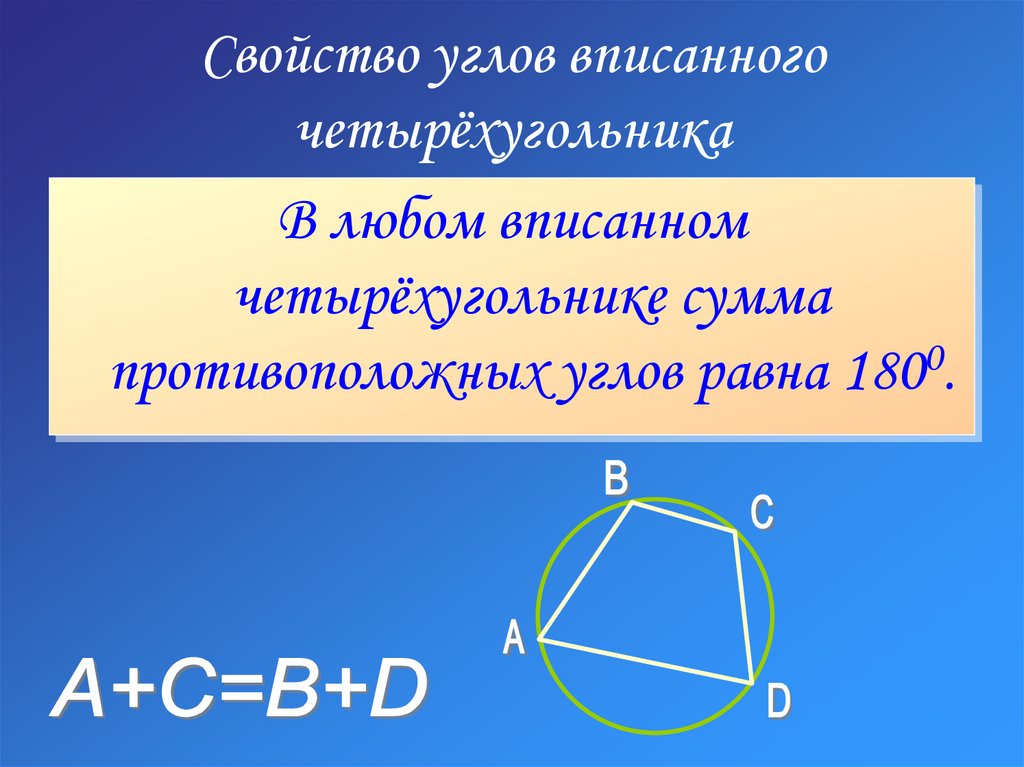
10. Свойство углов вписанного четырёхугольника

В любом вписанном
четырёхугольнике сумма
противоположных углов равна 1800.

11. Сформулируйте обратное свойство:

Если сумма противоположных
углов четырёхугольника равна
0
180 , то вокруг него можно
описать окружность.

12. Выполните упражнения:

703
705 а
Домашнее задание:
702
705 б
*
689