Similar presentations:
Как называются квадратные уравнения, если а=1?
1.
18.03.2020Открытый урок алгебры в 8 а классе
2.
Решите кроссворд!1. Как называются квадратные
уравнения, если а=1.
2. Определитель числа корней
квадратного уравнения.
3. Как называются квадратные
уравнения, если в=0 или с=0.
4. Если в теореме поменять
местами условие и
заключение, то получится
теорема … данной.
3.
Теорема Виета4.
По праву достойна встихах быть воспета
О свойствах корней
теорема Виета.
5.
Выбери приведенныеквадратные уравнения
1.
2.
3.
4.
5.
6.
х2-5х+6=0
2х2+3х+1=0
х2-2х-15=0
3х2-7х+3=0
х2+6х+8=0
х2+3х-10=0
2
x +px+q=0
• 1. x2-5x+6=0
2
• 3. x -2x-15=0
2
• 5. x +6x+8=0
• 6. х2+3x-10=0
6.
Можно ли назвать корни этихуравнений, не вычисляя по формулам ?
2
•х +157х-158=0
2
х -2020х-2021=0
Можно ли определить сумму и
произведение корней уравнения, не зная
сами корни?
7.
Заполните таблицуx2+px+q=0
Уравнение
х2-5х+6=0 х2-2х-15=0 х2+6х+8=0
Корни уравнения
Коэффициент
p
Сумма корней
x1+x2
Коэффициент q
Произведение корней
x1 x2
8.
Проверьте себяx2+px+q=0
Уравнение
Корни
уравнения
Коэффициент p
Сумма корней
х1 + х2
Коэффициент q
Произведение
корней х1 х2
Х2-5х+6=0
Х2-2х-15=0
Х2+6х+8=0
2; 3
-3; 5
-2; -4
-5
5
-2
2
6
-6
6
6
-15
-15
8
8
9.
Заполните пропускиприведенного
Сумма корней
-------------квадратного уравнения равна
второму коэффициенту,
взятому
с
противоположным
знаком
-------------------------------------------------------,
произведение
а –-----------------------корней равно свободному члену.
10.
Заполните пропускиСумма
----------корней приведенного квадратного
уравнения
второму
равна -------------- коэффициенту, взятому
с противоположным знаком,
а произведение корней равно
свободному члену
---------------------------.
11.
Доказательство в общем виде12.
Теорема Виета.Если числа х1 и х2
являются корнями уравнения
х2+рх+q=0
то справедливы формулы
x1 x2 q
x1 x2 p
т.е.сумма корней приведённого квадратного
уравнения равна второму коэффициенту,
взятому с противоположным знаком, а
произведение корней равно свободному члену.
Проверка, правильно ли найдены корни уравнения.
13.
Назовите сумму корней,произведение корней
• -2х-15=0
• х2 +8х+15=0
2
• х -15х-8=0
• х2+2х-15=0
2
• х +2х+15=0
2
х
14.
15.
Зная, что х1 и х2- корни квадратногоуравнения, применяя теорему Виета,
составьте квадратные уравнения:
х1
х2
4
-3
5
2
-3
-6
8
12
х1+х2
х1 х2
уравнение
16.
Теорема, обратная теоремеВиета.
Если числа
таковы, что
p, q, x1 , x2
x1 x2 p, x1 x2 q
то x1 и x2 - корни уравнения
x px q 0
2
Доказательство рассмотреть самостоятельно.
17.
Определение знака корней.x px q 0
2
x1 x2 q
x1,2 < 0
D<0
D>0
q>0
корни одного знака
-p<0
а=1
-p>0
q<0
корни разного знака
x1 x2 p
x1,2 > 0
-p<0
Корней нет
-p>0
«─» у большего «+» у большего
по модулю корня по модулю корня
18.
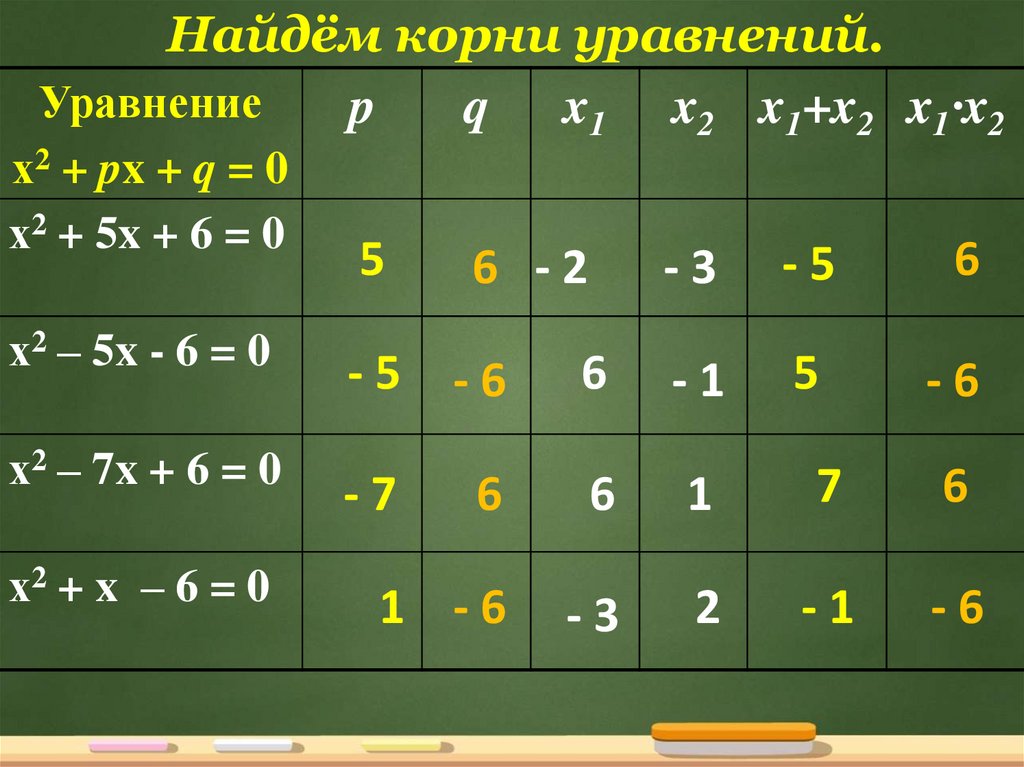
Найдём корни уравнений.Уравнение
p
q x1 x2 x1+x2 x1∙x2
х2 + px + q = 0
х2 + 5x + 6 = 0
х2 – 5x - 6 = 0
х2 – 7x + 6 = 0
х2 + x – 6 = 0
5
6 -2
-3
-5
6
5
-6
-5
-6
6
-1
-7
6
6
1
7
6
1 -6
-3
2
-1
-6
19.
20.
2х +157х-158=0
2
х -2020х-2021=0
21.
С какой проблемой вы столкнулись вначале урока?
С помощью чего удалось решить
проблему?
Можно ли все приведенные уравнения
решать по тереме обратной теореме
Виета?
Можно ли неприведенное квадратное
уравнение решить по теореме
обратной теореме Виета?
22.
День счастья –20.03.20
Флешмоб Российского
движения
школьников.


















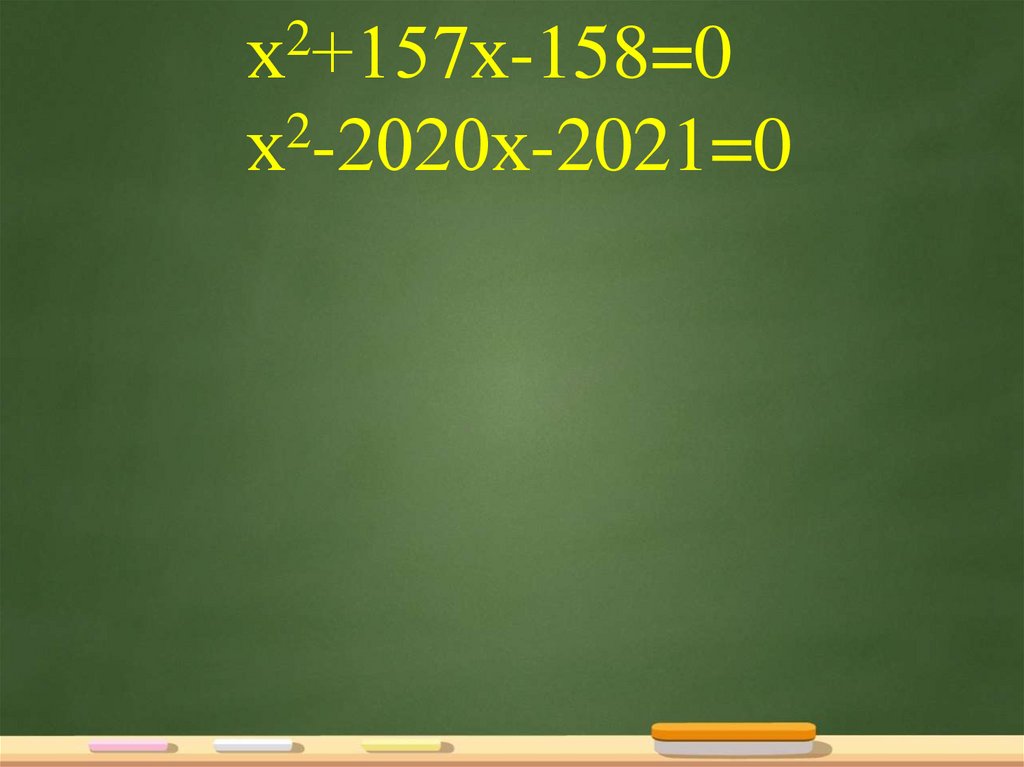


 mathematics
mathematics








