Similar presentations:
Деление рациональных чисел
1. Деление рациональных чисел
Баранова Татьяна Александровна,учитель математики
МБОУ «Средняя школа №1»
города Велижа
2. Девиз: «Просто знать – мало, знания нужно уметь использовать».
ДЕВИЗ: «ПРОСТО ЗНАТЬ – МАЛО, ЗНАНИЯНУЖНО УМЕТЬ ИСПОЛЬЗОВАТЬ».
Сегодня на уроке.
Учебные
Анализировать….
Вычислять…
Объяснять…
Обобщать…
Описывать…
Осуществлять
Повторять…
Отработать…
Познавательные
Опознавать…
Характеризовать…
Выяснять…
Использовать…
Владеть…
3.
Вопросы для повторения• Как сравнить рациональные числа?
• Чему равен модуль положительного
числа?
• Чему равен модуль
отрицательного числа?
• Как умножить рациональные
числа?
• Как сложить два отрицательных
числа?
• Как сложить два числа с разными
знаками?
4.
Сравните значениявыражений
>и
<и
и
<
>и
5.
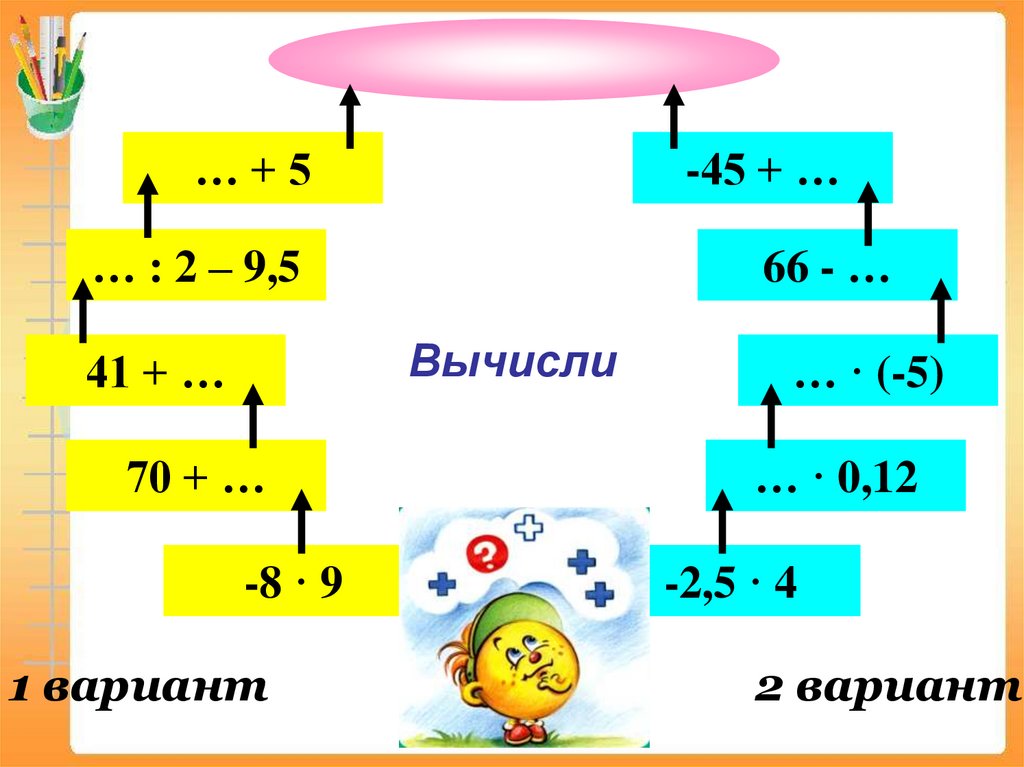
…+5-45 + …
… : 2 – 9,5
66 - …
Вычисли
41 + …
70 + …
-8 · 9
1 вариант
… · (-5)
… · 0,12
-2,5 · 4
2 вариант
6.
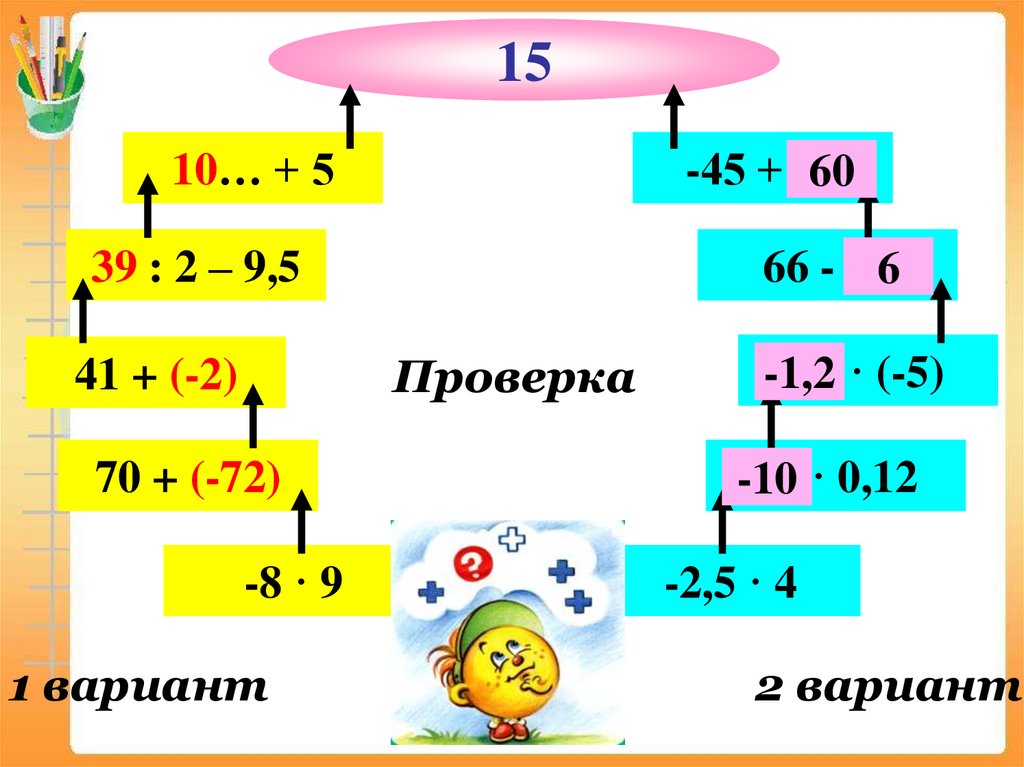
1510… + 5
-45 + …
60
39 : 2 – 9,5
66 - …6
Лесенка
Проверка
41 + (-2)
70 + (-72)
-8 · 9
1 вариант
… · (-5)
-1,2
… · 0,12
-10
-2,5 · 4
2 вариант
7.
Сравните числа:8.
Делениерациональных
чисел
9. Определим знак частного
+-
-
+
10. Алгоритм деления рациональных чисел
1)Определить знак частного2)Разделить модуль делимого на
модуль делителя.
11.
Сравните числа:12. Найдите частное
варианты ответов-38:19 = …
45:(-15) = …
-5,1:(-17) = …
-4,4:4 = …
-8,6:(-4,3) = …
48,1:(-48,1) = …
-950:9,5 = …
-5,42:(-27,1) = …
10,01:(-1,3) = …
2; -2; -0,2
-3; 3; -5
0,3; -0,03; -0,3
11; -1,1; 1,1
0,2; -2; 2
-1; 0; 1
-100; 10; -10
-0,2; 0,2; 0,3
-7,7; 12,7; -9,7
13. Верно ли выполнено деление ?
варианты ответов34:(-2) = 17
-60:1,5 = -4
-7,6:(-4) = 1,9
2,7:(-2,7) = 0
-1:(-5) = 0,2
8,5:(-1) = 8,5
да;
да;
да;
да;
да;
да;
нет
нет
нет
нет
нет
нет
14.
Физкультминутка15. Примеры учат не меньше, чем правило
ПРИМЕРЫ УЧАТ НЕ МЕНЬШЕ, ЧЕМПРАВИЛО
Работа с учебником
№1124;№1126
16.
Самостоятельная работа1 вариант.
2 вариант.
4,5 : (–0,5) =
3,5 : (– 0,5) =
(–0,56) : (–1,4) =
(–0,45) : (–0,5) =
–4,8 : 12 =
44
11 :
52
28
: 7
51
–2,6 : 13 =
34
17 :
41
24
: 4
71
17.
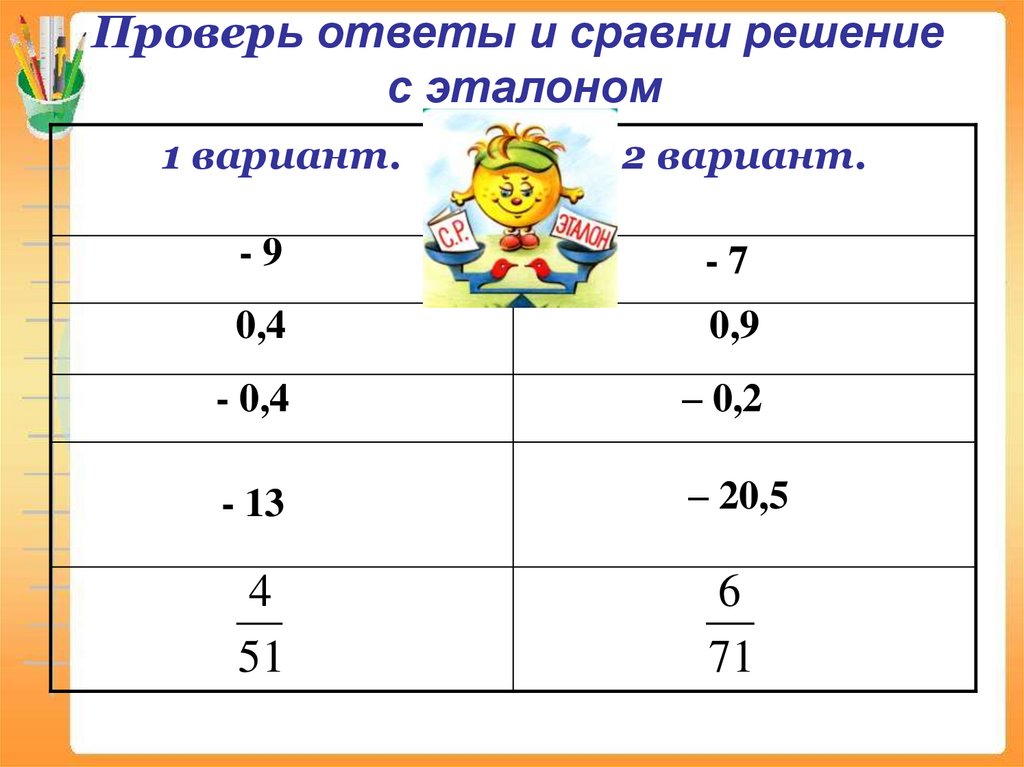
Проверь ответы и сравни решениес эталоном
1 вариант.
2 вариант.
-9
-7
0,4
0,9
- 0,4
– 0,2
- 13
– 20,5
4
51
6
71
18. Итог урока
– Что нового узнали на уроке?
– Какую цель мы ставили в начале урока?
– Проанализируйте свою работу на уроке.
- В чем было затруднение?
- Поблагодарите одноклассников, которые
помогли получить результат урока.
19.
Индийские математики представляли себеположительные числа как «имущества», а
отрицательные числа как «долги».
Вот как индийский математик Брахмагупта (VIIв)
излагал правила сложения и вычитания: «Сумма
двух долгов есть долг», «Сумма двух
имуществ есть имущество», «сумма
имущества и долга равна их разности» и т.д.
Попробуйте и вы на досуге сформулировать
правила деления положительных и
отрицательных чисел на «языке Брахмагупты»
20.
Домашнее задание§ 40, вопросы 1–3,
№ 1125, №1127,
сообщение о Луке Пачоли
21.
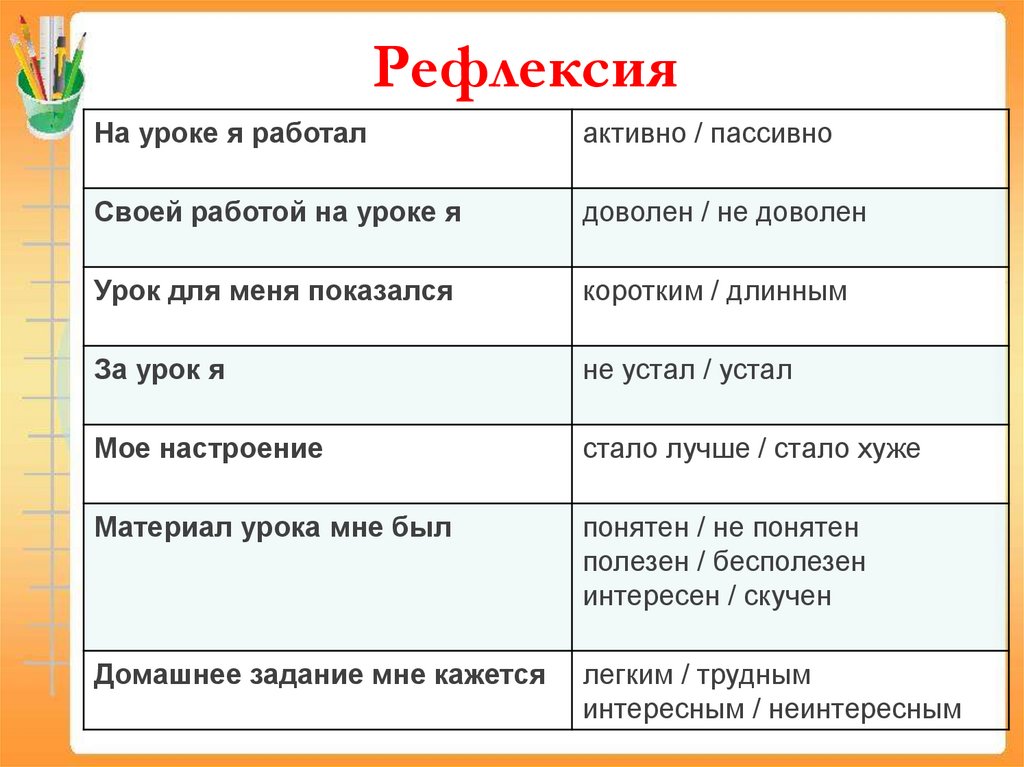
РефлексияНа уроке я работал
активно / пассивно
Своей работой на уроке я
доволен / не доволен
Урок для меня показался
коротким / длинным
За урок я
не устал / устал
Мое настроение
стало лучше / стало хуже
Материал урока мне был
понятен / не понятен
полезен / бесполезен
интересен / скучен
Домашнее задание мне кажется
легким / трудным
интересным / неинтересным


















 mathematics
mathematics








