Similar presentations:
Метод интервалов. Алгоритм решения системы уравнений графическим способом
1. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их
систем2. Метод интервалов.
3. Что такое метод интервалов Метод интервалов — это специальный алгоритм, предназначенный для решения сложных неравенств
Что такое метод интерваловМетод интервалов — это специальный алгоритм,
предназначенный для решения сложных неравенств
вида f (x) > 0 и f (x) < 0. Алгоритм состоит из 4 шагов:
1. Решить уравнение f (x) = 0. Таким образом, вместо
неравенства получаем уравнение, которое решается намного
проще;
2. Отметить все полученные корни на координатной прямой.
Таким образом, прямая разделится на несколько интервалов;
3. Выяснить знак (плюс или минус) функции f (x) на самом
правом интервале. Для этого достаточно подставить в f (x)
любое число, которое будет правее всех отмеченных корней;
4. Отметить знаки на остальных интервалах. Для этого
достаточно запомнить, что при переходе через каждый
корень знак меняется.
4. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем
5.
у = kx+b - прямаяy
0
x
b
6. y = ax2 + bx + c –
y=2
ax +
парабола
а>0
а<0
y
0
bx + c –
y
x
0
x
7.
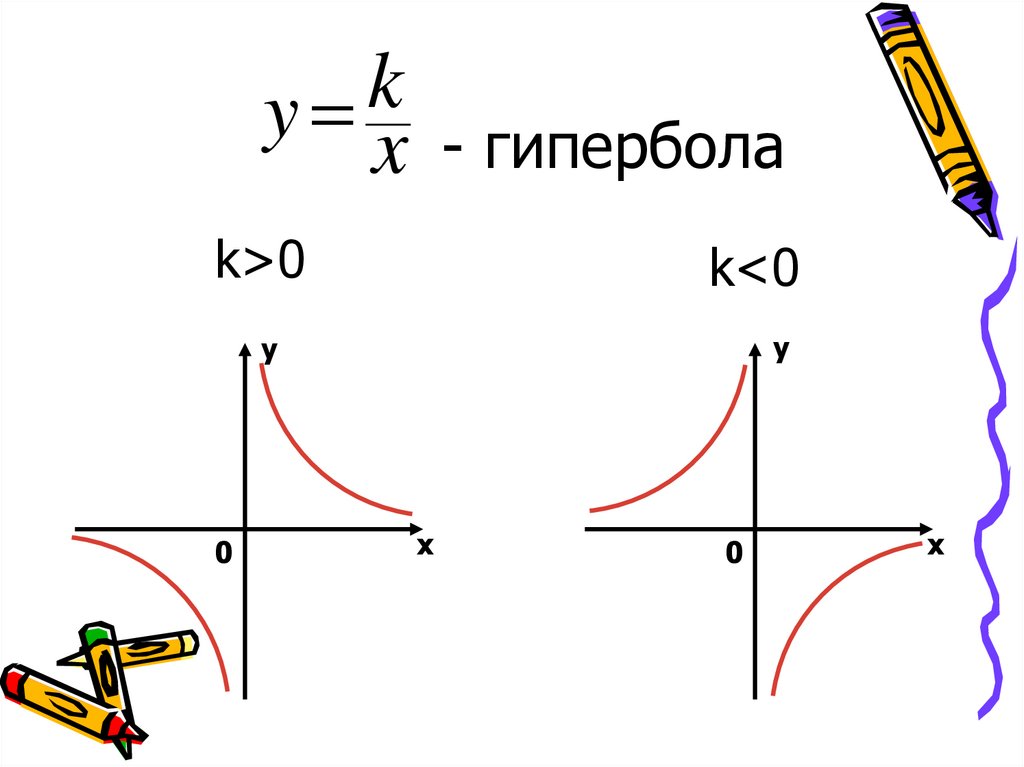
ky x
- гипербола
k>0
k<0
y
y
0
x
0
x
8.
(x a)2 ( y b)2 R2- окружность
R – радиус
(a,b) – координаты центра
y
R
0
x
9.
Графиком уравнения с двумяпеременными
называется множество всех точек
координатной плоскости,
координаты которых служат
решениями данного уравнения.
10.
Решением линейного неравенствас двумя переменными
называется любая упорядоченная
пара (х; у), которая обращает
заданное неравенство с
переменными в верное числовое
неравенство.
11.
y>f(x)y<f(x)
12.
y f (x)y f (x)
13. Алгоритм решения системы уравнений графическим способом:
1). Построить в одной системе координатграфики уравнений системы.
2). Найти приближённые значения
координат точек пересечения
графиков.
3). Если возможно, с помощью проверки
уточнить решения системы.
14.
y f ( x),y g ( x).
15.
2Решите уравнение: y x 4
3
16. Решите уравнение:
4Решите уравнение: y x 2
5
17.
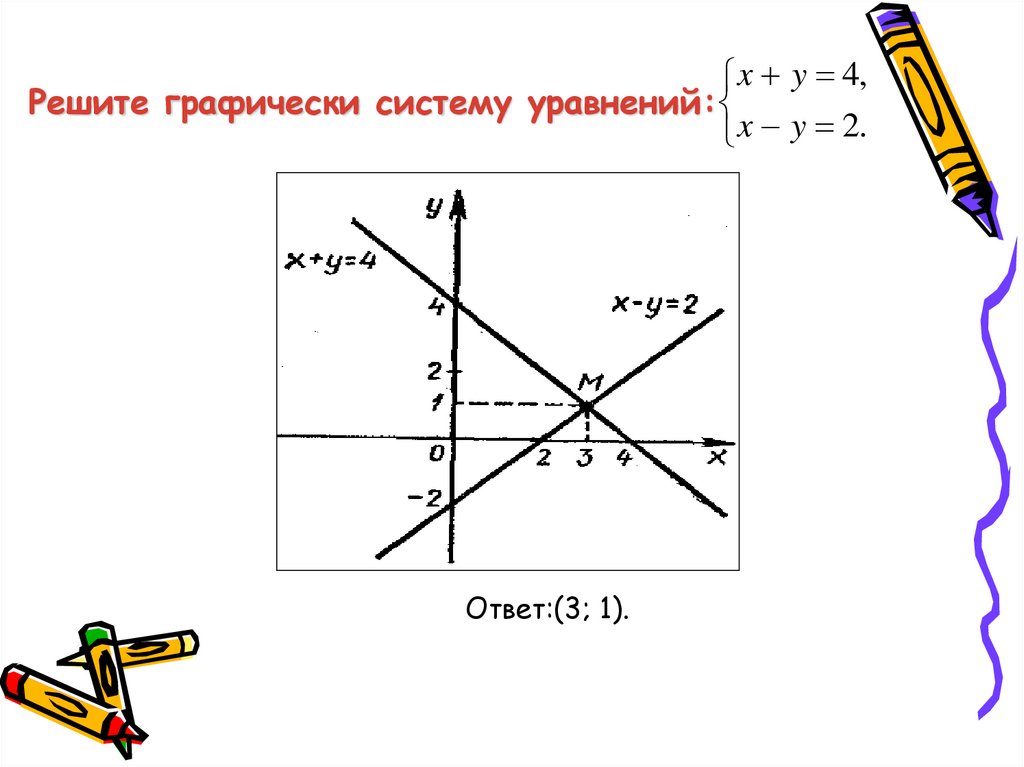
x y 4,Решите графически систему уравнений:
x y 2.
Ответ:(3; 1).
18.
Изобразите на координатной плоскостимножество решений неравенств:
a) y<х2;
б) у<2;
у
в) x -2.
у
у=х2
у
у=2
x=-2
0
х
0
х
0
х
19.
Изобразите на координатной плоскости множестворешений системы неравенства:
x y 9,
2
2
x
y
25.
2
2
у
х2+у2=25
х2+у2=9
0
3
5
х
20. Практическая часть
• Задача 1. Решите неравенство:x(2x + 8)(x − 3) > 0
• Задача 2. Решите неравенство:
(x + 9)(x − 3)(1 − x) < 0
• Задача 3. Решите неравенство:
(x − 2)(x + 7) < 0
21. Практическая часть
y x 2 1,5x 2
y 0
Практическая часть
• Задача 4. Изобразите все точки с
координатами (х;у), для которых
выполняется равенство.
1. (х-1)(2у-3)=0
2. (х-у)(х2-4)=0
• Задача 5. Решить систему графическим
способом:
y x 2 1
,5x 2
y 0





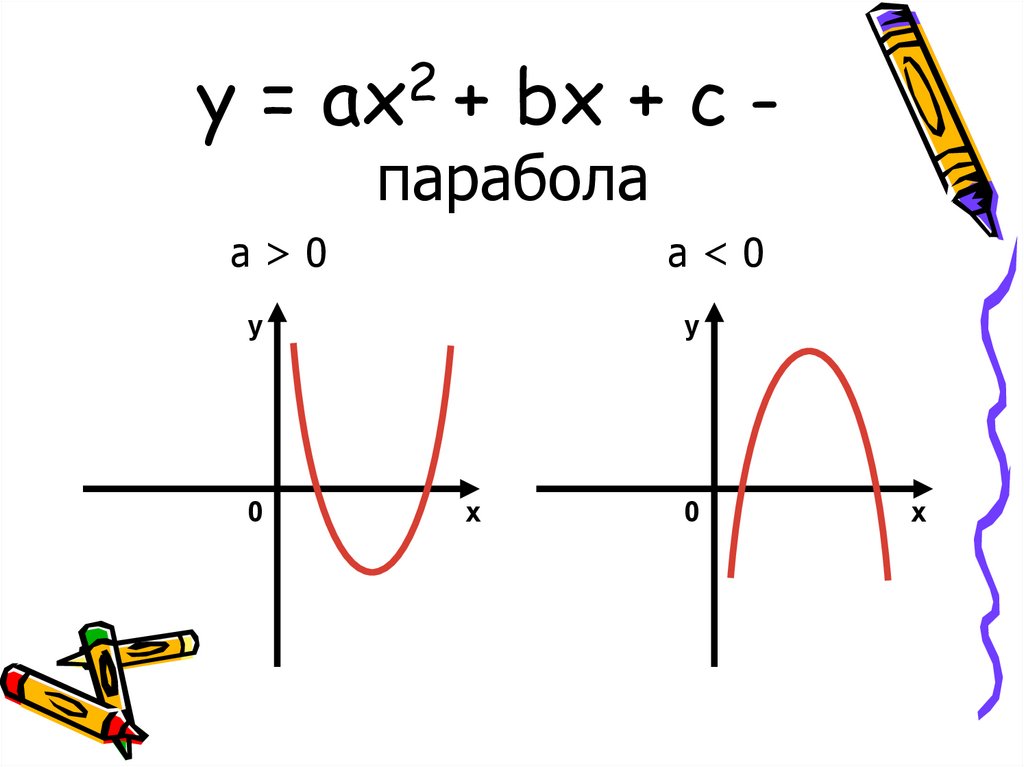













 mathematics
mathematics