Графический метод решения системы уравнений с двумя переменными

1.

Математика уступает
Свои крепости лишь
Сильным и смелым
А.П. Конфорович
‘Графический метод решения
системы уравнений с двумя
переменными’

2. Цель урока: Научить решать систему уравнений с двумя переменными графическим методом. Рассмотреть частные случаи решения

системы линейных уравнений.

3. Что называют системой уравнений? Рассмотрим два линейных уравнения: 1) y – 2x = – 3 2) x + y = 3

Системой уравнений называется некоторое
количество уравнений, объединенных фигурной
скобкой. Фигурная скобка означает, что все
уравнения должны выполняться одновременно.
a1 x b1 y c1 ,
a2 x b2 y c2 .
y – 2x = – 3
x+y=3

4.

Каждая пара значений переменных, которая
одновременно является решением всех
уравнений системы, называется решением
системы.
Решением системы уравнений с двумя
переменными называется пара значений
переменных, обращающая каждое уравнение
системы в верное равенство.
Решить систему уравнений - значит найти все её
решения или установить, что их нет.

5.

Решение системы графическим способом
у – х = 2,
у + х = 10;
Выразим у
через х
y
y=x+2
10
у = х + 2,
у = 10 – х;
Построим график первого уравнения
6
у=х+2
х 0 -2
у 2 0
y=10 - x
2
1
Построим график второго уравнения
у = 10 – х
х 0 10
у 10 0
-2
0
1
Ответ: (4; 6)
4
10
x

6. Алгоритм решения системы уравнений графическим способом

1. Приводим оба уравнения к виду линейной функции
y = k x + m.
2. Составляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной плоскости.
4. Определяем число решений:
Если прямые пересекаются, то одно решение пара чисел (х ; у) –
координаты точки пересечения;
Если прямые параллельны, то нет решений;
Если прямые совпадают, то бесконечно много решений.
5. Записываем ответ.

7. Графический метод решения системы x + y = 3 y – 2x = – 3

Графический метод решения системы
у =3–x
x
y
0
3
3
0
A(0;3)
M(2;1)
у =1
у = 2x – 3
D(3;3)
B(3;0)
X=2
x
y
0
3
–3
3
C(0; – 3)
Ответ: (2; 1)
x+y=3
y – 2x = – 3

8.

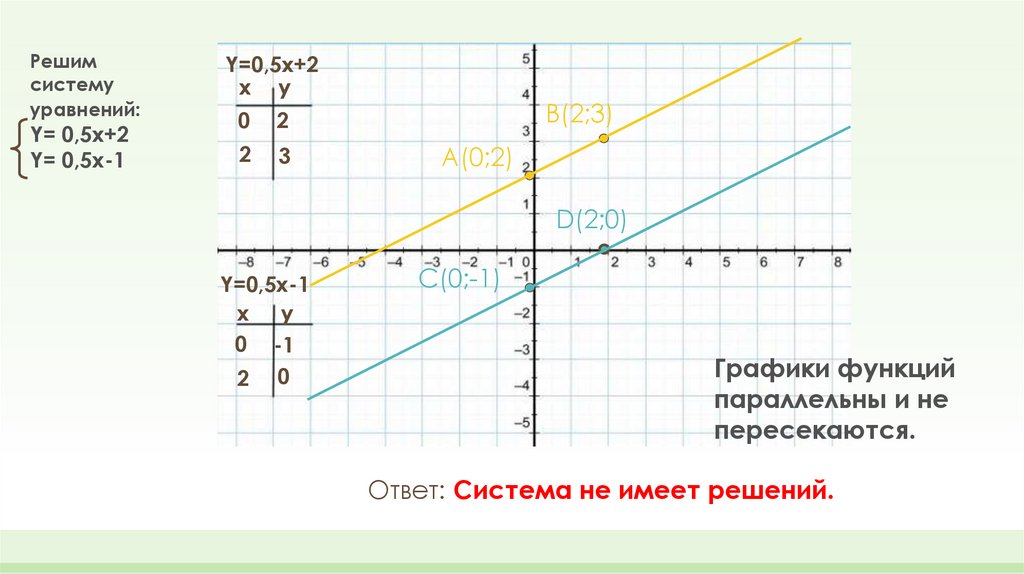
Решим
систему
уравнений:
Y= 0,5x+2
Y= 0,5x-1
Y=0,5x+2
x y
0
2
2
3
B(2;3)
A(0;2)
D(2;0)
Y=0,5x-1
x y
0 -1
2 0
C(0;-1)
Графики функций
параллельны и не
пересекаются.
Ответ: Система не имеет решений.

9.

Y=x+3
x
y
0
3
-3
0
D(1;4)
Система
Y=x+3
A(0;3)
Y=x+3
C(-1;2)
B(-3;0)
Y=x+3
x y
1
4
-1
2
Графики функций
совпадают.
Ответ: система имеет бесконечное множество решений

10.

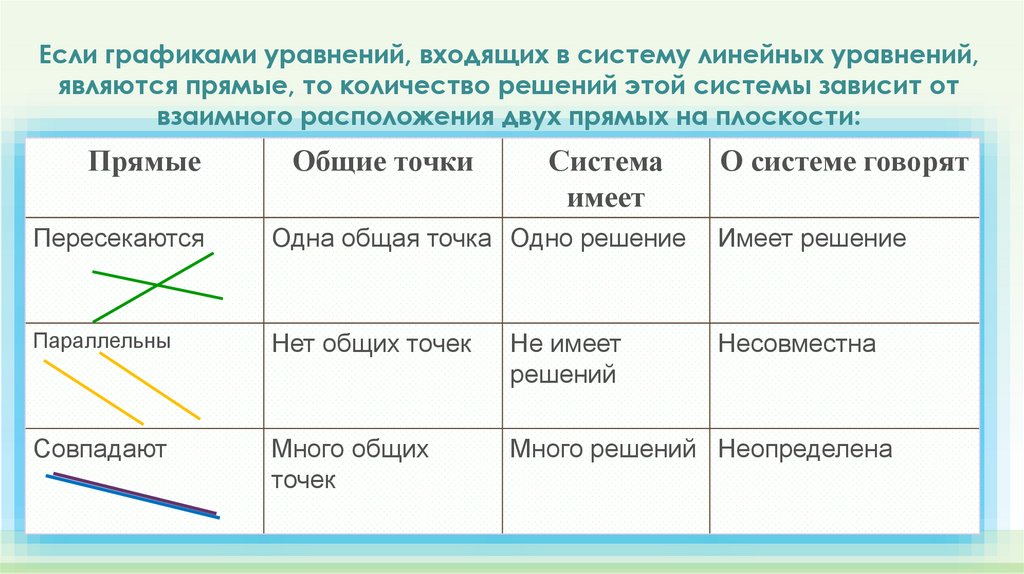
Если графиками уравнений, входящих в систему линейных уравнений,
являются прямые, то количество решений этой системы зависит от
взаимного расположения двух прямых на плоскости:
Прямые
Общие точки
Система
имеет
О системе говорят
Пересекаются
Одна общая точка Одно решение
Имеет решение
Параллельны
Нет общих точек
Не имеет
решений
Несовместна
Совпадают
Много общих
точек
Много решений Неопределена

11.

Частные случаи пересечения графиков линейных
функций (памятка)

12.

2) Решите систему уравнений:
х у 1,
2 х у 4.
у
1) х – у = -1,
у=х+1
х у
0 1
2 3
2) 2х + у = 4,
у = 4 - 2х
х у
0 4
2 0
Ответ: х = 1, у = 2.
4
3
2
1
1
1
2
3
х

13.

1) Решите систему уравнений:
1) 3х +2у = 7,
2у = 7 - 3х,
у = (7 - 3х):2,
у = 3,5 -1,5х,
у = -1,5х + 3,5.
у х
1 2
3 -1
Ответ: х = 3, у = -1.
3х 2 у 7,
2 х 4 у 2.
2) 2х + 4у = 2,
4у = 2 - 2х,
у = (2 - 2х):4,
у = 0,5 – 0,5х.
х
1
3
у
0
-1
у
4
3
2
1
1
1
2
3
х

14. Решите систему уравнений графическим способом

1 вариант
у = 2х - 3
у=-х+3
2 вариант
у = 3х - 4
у = 0,5х + 1

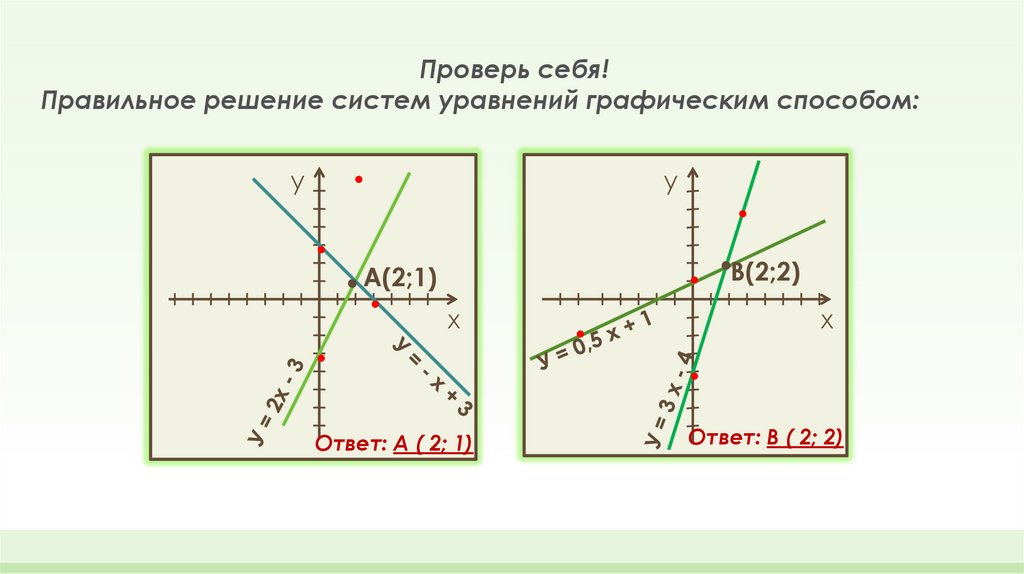
15.

Проверь себя!
Правильное решение систем уравнений графическим способом:
.
у
.
.
. А(2;1)
.
у
х
Ответ: А ( 2; 1)
.
.
.
.
.В(2;2)
х
Ответ: В ( 2; 2)

16. Домашнее задание:

§ 26, выучить материал со слайдов
3, 4, 6,10 (переписать в рабочую
тетрадь)
№ 1008, 1010(1)