Применение информационных технологий при решении задач с помощью определенного интеграла

1.

ТЕМА ЗАНЯТИЯ:

2.

ЦЕЛИ ЗАНЯТИЯ:
Составить формулу для нахождения площади криволинейной
трапеции в зависимости от ее вида.
Вычислить определенный интеграл.
Построить графики нескольких функций в одной системе
координат с помощью MS Excel.
Используя возможности MS Paint и MS Word, оформить отчет к
практической работе.
Вывести отчет на печать через сетевое окружение.

3.

«Сближение теории с практикой даёт
самые благотворные результаты, и
не одна только практика от этого
выигрывает, сами науки развиваются
под её влиянием, она открывает им
новые предметы для исследования или
новые стороны в предметах давно
известных».
Чебышев П.Ф.

4.

ПОНЯТИЕ ПЕРВООБРАЗНОЙ И
НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Функция y = F(x) называется первообразной для функции y = f(x) на
заданном числовом промежутке I, если для всех значений аргумента,
принадлежащих этому промежутку, выполняется равенство: F’(x) = f(x).
Любая первообразная на заданном промежутке имеет вид: F(x)+ C, где
F(x) – некоторая первообразная, а C- произвольная постоянная).
Множество всех первообразных функции y = f(x) на заданном числовом
промежутке I называется неопределенным интегралом функции f(x) и
обозначается
Процесс
f ( x)dx F ( x) C
нахождения
всех
…………………………. функции f(x).
первообразных
функции
f(x)
называется

5.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Понятие определенного интеграла выводится через криволинейную
трапецию.
Криволинейной трапецией называется фигура, ограниченная линиями
y = f(x), y = 0, x=a, x=b. Площадь криволинейной трапеции выражается
интегральной суммой или числом, которое называется определенным
интегралом.
Определенный интеграл вычисляется по формуле Н………….…– Л……………..
b
f ( x)dx F ( x)
a
b
a
F (b) F (a)

6.

НАЙДИ И ИСПРАВЬ ОШИБКУ!
x
5
dx 5 x C
4
6
x
x dx 6 C
7
7 1
1
x
1 x dx 7
6
1
1 1
7 7

7.

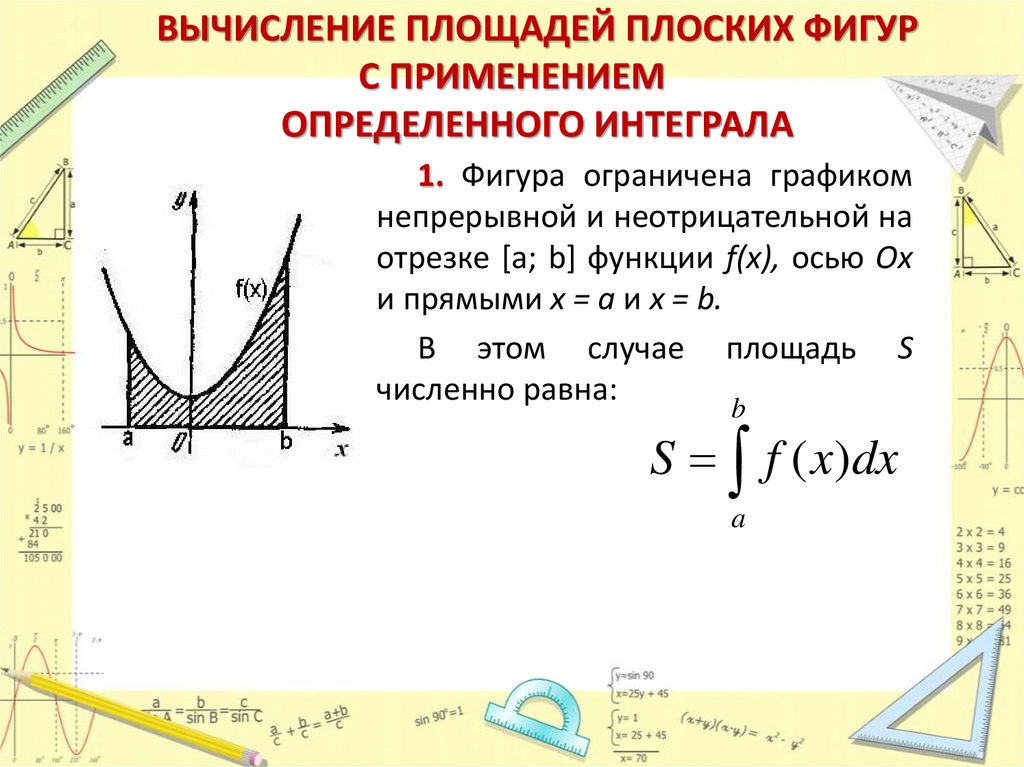
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
С ПРИМЕНЕНИЕМ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. Фигура ограничена графиком
непрерывной и неотрицательной на
отрезке [а; b] функции f(х), осью Ох
и прямыми х = а и х = b.
В этом случае площадь S
численно равна:
b
S f ( x)dx
a

8.

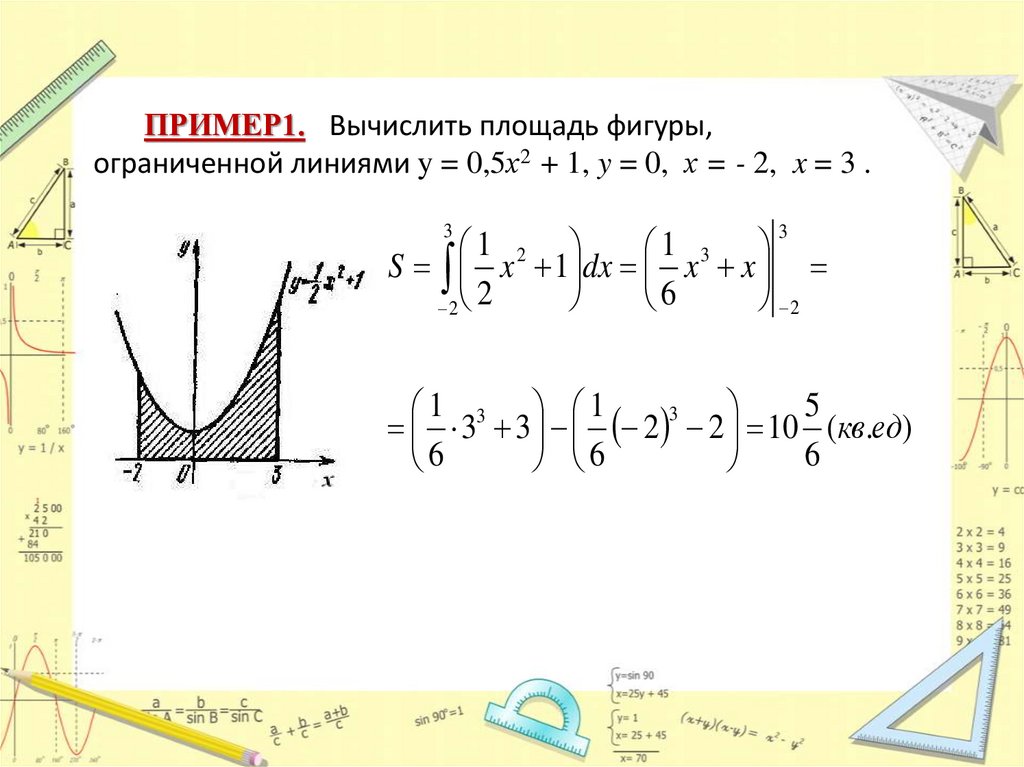
ПРИМЕР1. Вычислить площадь фигуры,
ограниченной линиями y = 0,5х2 + 1, y = 0, х = - 2, x = 3 .
3
1 2
1 3
S x 1 dx x x
2
6
2
2
3
5
1 3 1
3
3 3 2 2 10 (кв.ед)
6
6
6

9.

2. Фигура ограничена
графиками
двух
непрерывных на отрезке [а; b] функций f(х) и g(х) и
прямыми х= а, x=b, где f (х) ≥ g (х) и а ≤ x ≤ b .
В этом случае искомая
площадь S вычисляется по
формуле:
b
S f x g x dx
a

10.

Пример 2. Вычислить площадь фигуры, ограниченной
линиямиy 1 x 2 и y 1 x 2 .
3
9
Пределы интегрирования а и b находим из графика
функций:
1
1 3 6
1 2
1 2
S x 2 x dx x 2 x
x
3
27 3
9
6
3
6
1
1
1
1
2
3
62 2 6
63 3 2 3
3 13,5( кв.ед)
27
27
6
6

11.

ПРИМЕНЕНИЕ ИНТЕГРАЛА
РАБОТА ПЕРЕМЕННОЙ СИЛЫ
l2
A f (l )dl
где А - работа, F – сила.
l1
ПЕРЕМЕЩЕНИЕ ПРИ ПЕРЕМЕННОЙ СКОРОСТИ
b
S V (t )dt
где S - перемещение, V – скорость.
a
ОПРЕДЕЛЕНИЕ ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ
b
V S ( x)dx
a
где S - площадь сечения фигуры, V – объем.

12.

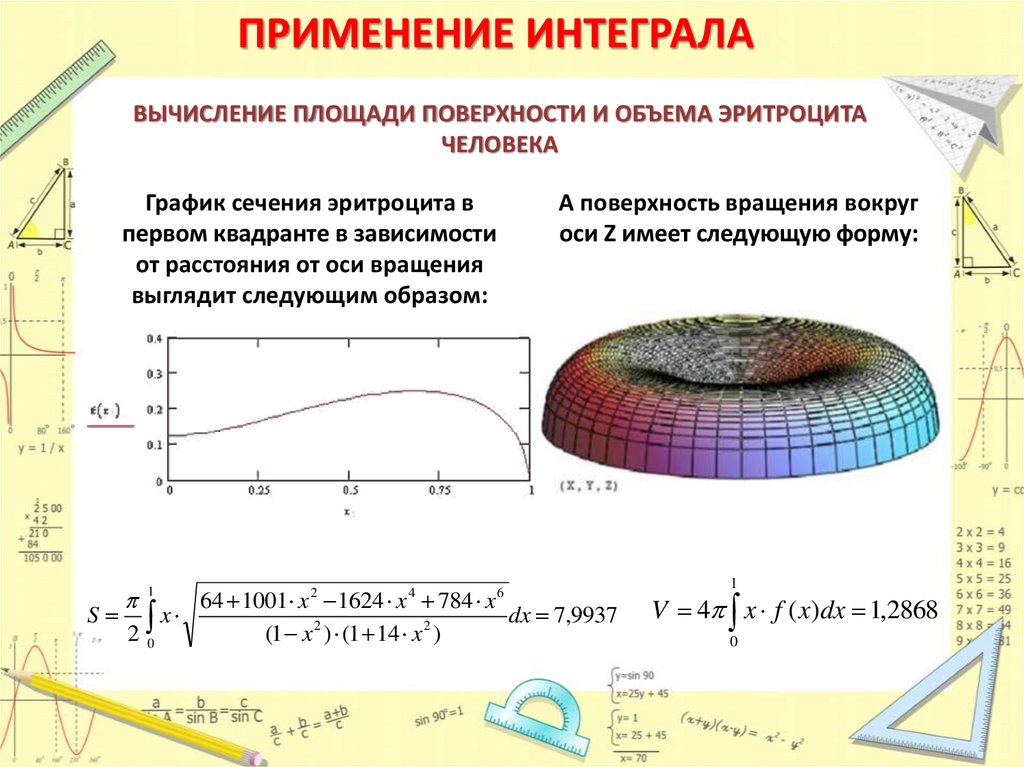
ПРИМЕНЕНИЕ ИНТЕГРАЛА
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ И ОБЪЕМА ЭРИТРОЦИТА
ЧЕЛОВЕКА
График сечения эритроцита в
первом квадранте в зависимости
от расстояния от оси вращения
выглядит следующим образом:
А поверхность вращения вокруг
оси Z имеет следующую форму:
64 1001 x 2 1624 x 4 784 x 6
S x
dx 7,9937
20
(1 x 2 ) (1 14 x 2 )
1
1
V 4 x f ( x)dx 1,2868
0

13.

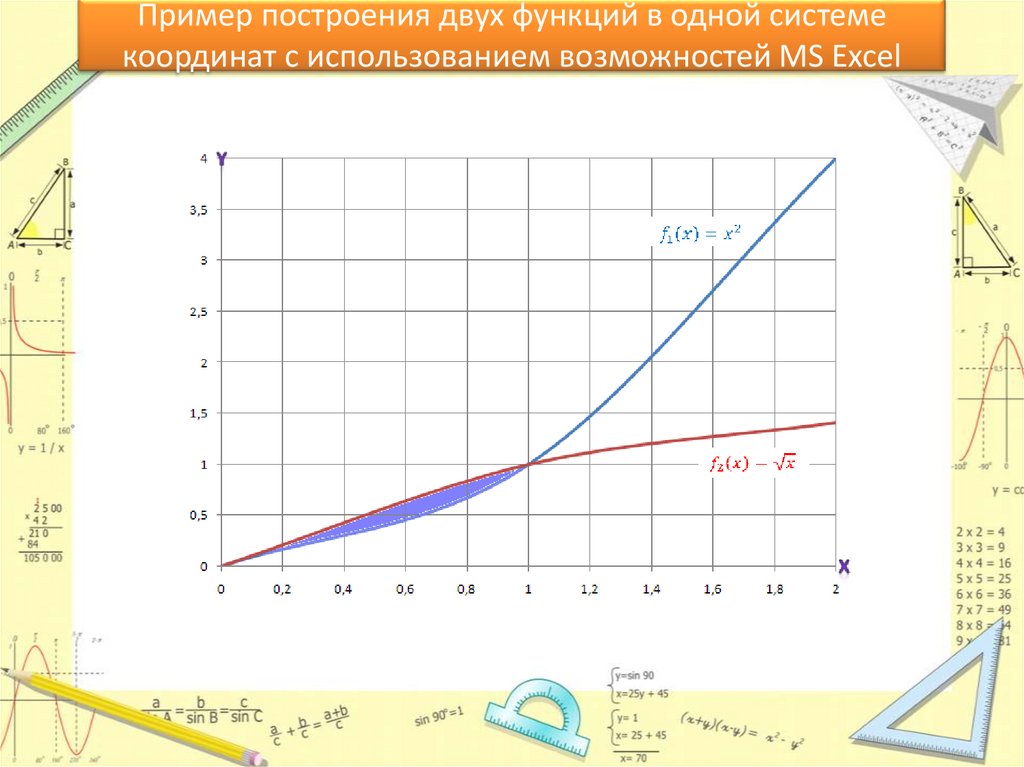
Пример построения двух функций в одной системе
координат с использованием возможностей MS Excel

14.

15.

Задание 1
Информатика
Построить график двух функций в одной системе координат с использованием
возможностей MS Excel.
Шаг на отрезке определить самостоятельно.
• Отформатировать график (смотреть образец отчета в папке «Отчет» на рабочем
столе).
• Сделать скриншот графика функций.
• В MS Paint залить область криволинейной трапеции, площадь которой необходимо
найти (смотреть образец отчета).
• Составить ОТЧЕТ к практической работе, используя возможности MS Word (смотреть
образец отчета).
• Вставить в ОТЧЕТ к практической работе полученное изображение криволинейной
трапеции в MS Paint (смотреть образец отчета).
Задание 2
Повторить шаги с 1 по 6.
Готовый ОТЧЕТ к практической работе распечатать самостоятельно.
Математика
Написать в ОТЧЕТЕ к практической работе вычисление площади построенной
криволинейной трапеции для двух заданий.

16.

Результаты практической работы
Компьютер
Компьютер 1:
Компьютер 2:
Компьютер 3:
Компьютер 4:
Компьютер 5:
Компьютер 6:
Студенты
Студент 1
Студент 2
Студент 1
Студент 2
Студент 1
Студент 2
Студент 1
Студент 2
Студент 1
Студент 2
Студент 1
Студент 2
Оценка по
математике
Оценка по
информатике