Similar presentations:
Определение производной (10 класс)
1.
Муниципальное бюджетное общеобразовательное учреждениесредняя общеобразовательная школа №1г. Гагарина Смоленской области
Определение производной
Автор Виноградова Галина
Владимировна
Гагарин 2017 г.
2.
§27.Определение производной.
3.
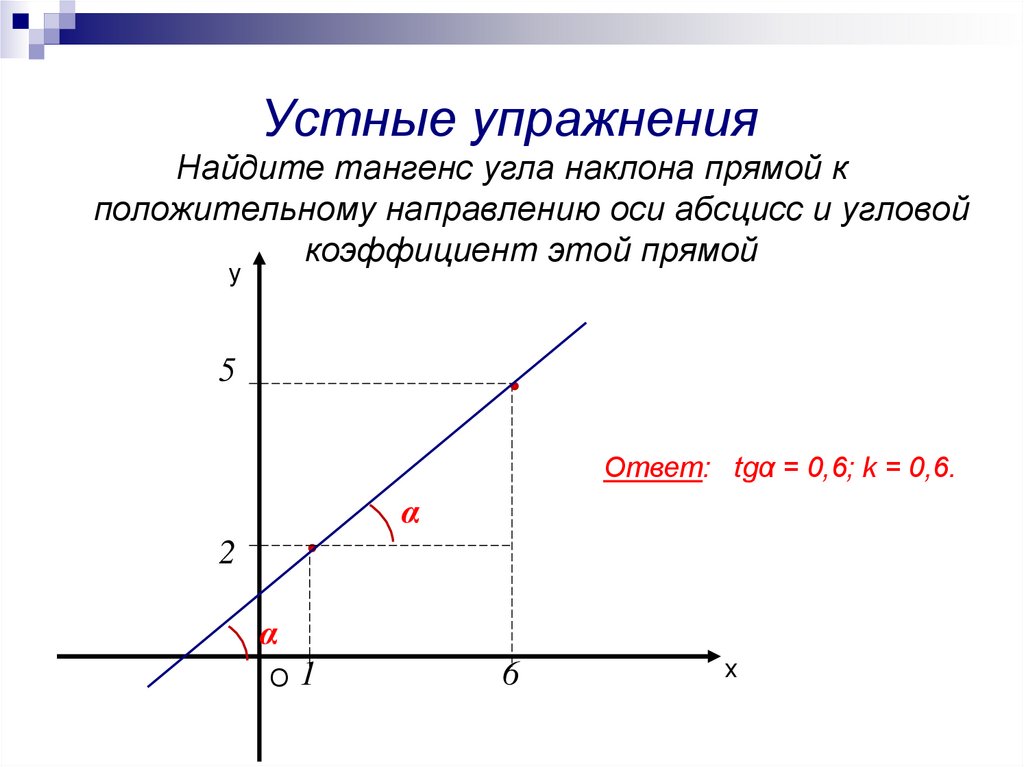
Устные упражненияНайдите тангенс угла наклона прямой к
положительному направлению оси абсцисс и угловой
коэффициент этой прямой
у
5
Ответ: tgα = 0,6; k = 0,6.
α
2
α
О
1
6
х
4.
Устные упражненияНайдите тангенс угла наклона прямой к
положительному направлению оси абсцисс и угловой
коэффициент этой прямой
у
5
Ответ: tgα = -0,6; k = -0,6.
2
α
О
1
6
х
5.
Определение 2 (§26)∆х = х1 – х0 – приращение аргумента
∆y = f(x0 + ∆х) - приращение функции
у
у = f(x)
f(х0 + ∆x)
∆y
f(х0)
О
P
M
х0
∆x
х1
х
6.
1. Задачи, приводящие кпонятию производной.
7.
Задача 1 ( о скорости движения)∆s
s = s(t)
х
М
P
О OM = s(t)
OP = s(t + ∆t)
MP = OP – OM = s(t + ∆t) – s(t) = ∆s
vср.
s
м / с
t
s
v Lim
м / с
t 0 t
8.
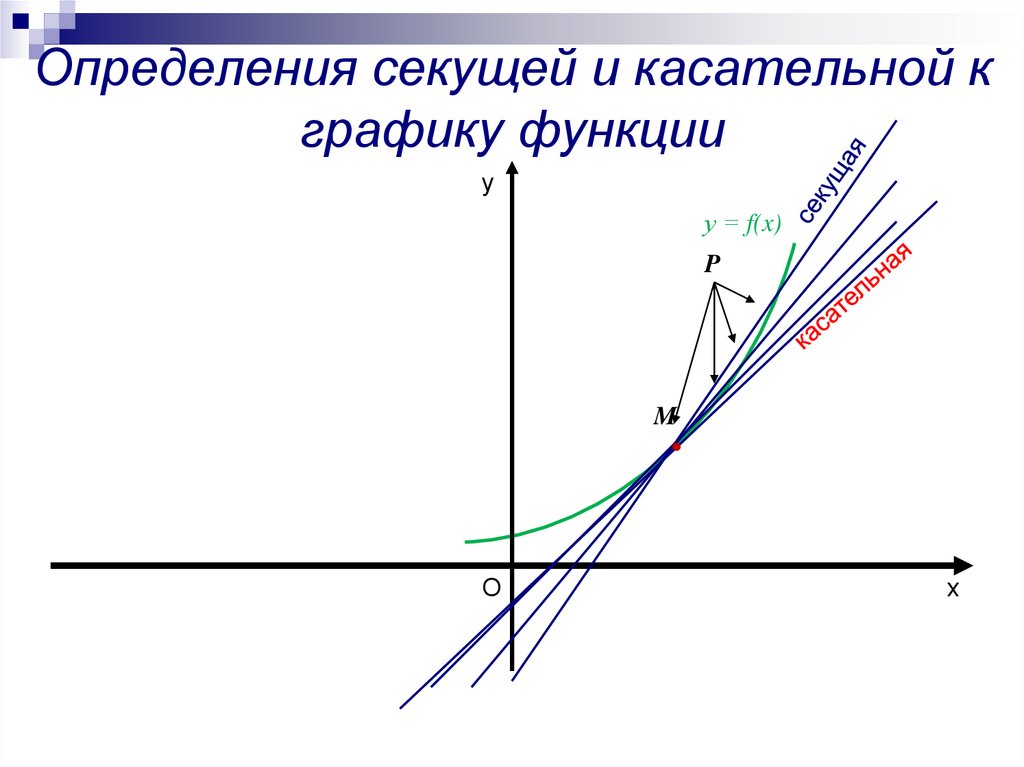
Определения секущей и касательной кграфику функции
у
у = f(x)
P
M
О
х
9.
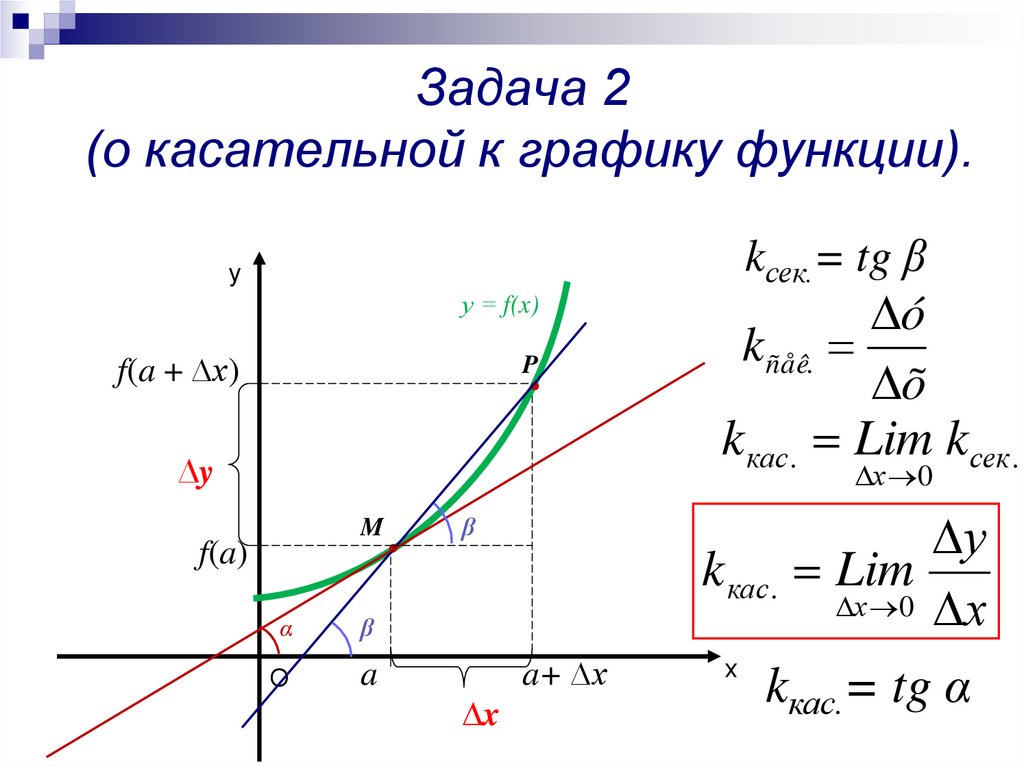
Задача 2(о касательной к графику функции).
kсек.= tg β
у
у = f(x)
f(a + ∆x)
P
∆y
ó
kñåê.
õ
k кас. Lim kсек .
х 0
M
f(a)
α
β
О
a
β
a+ ∆x
∆x
у
k кас. Lim
х 0 х
х
kкас.= tg α
10.
2. Определениепроизводной.
11.
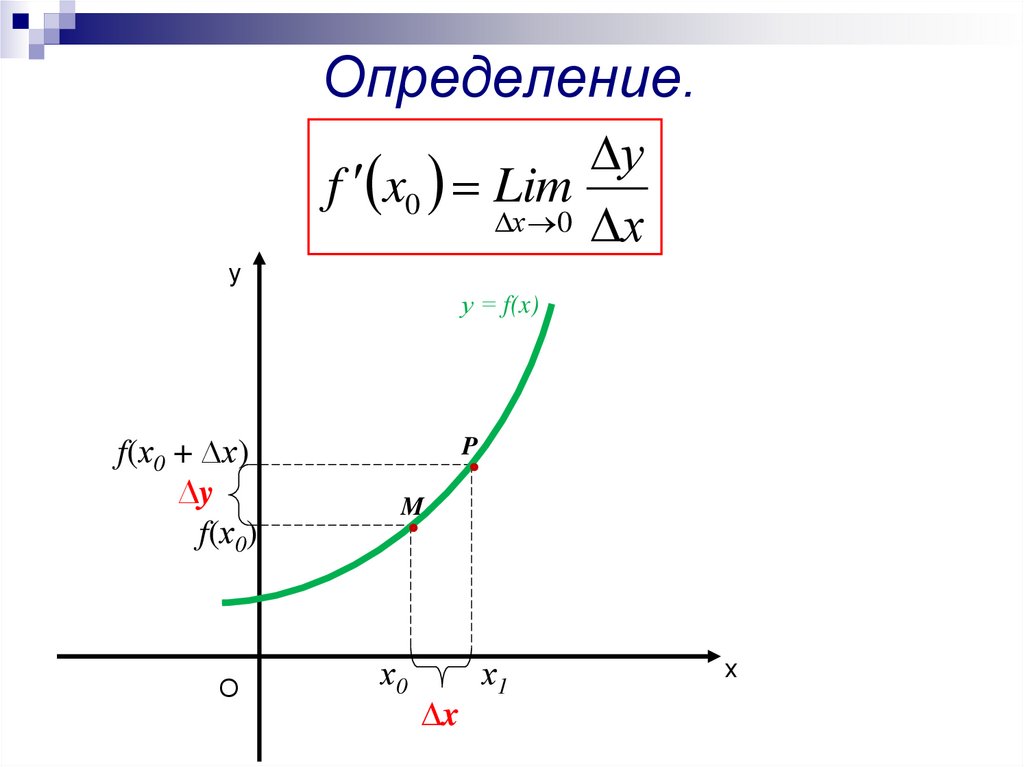
Определение.у
f x0 Lim
х 0 х
у
у = f(x)
f(х0 + ∆x)
∆y
f(х0)
О
P
M
х0
∆x
х1
х
12.
Физический смысл производнойs = s(t)
О
М
v(t ) s (t )
х
13.
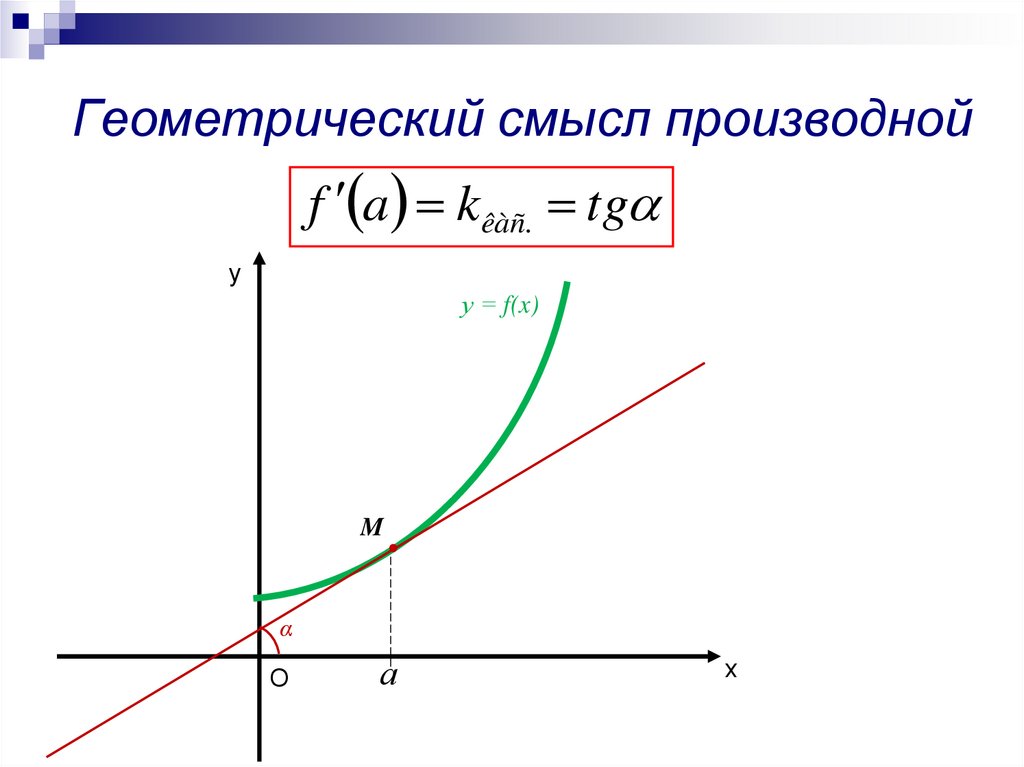
Геометрический смысл производнойf a kêàñ. tg
у
у = f(x)
M
α
О
а
х
14.
Алгоритм нахождения производнойфункции у = f(x)
1.
Зафиксировать значение х, найти f(x).
2.
Дать аргументу приращение Δх, перейти в новую
точку х + Δх, найти f(x + Δх).
3.
4.
5.
Найти приращение функции Δу = f(x + Δх) - f(x).
у
.
Составить отношение
х
у
.
Вычислить Lim
х 0 х
Этот предел и есть f’(x).
15.
3. Примеры применениягеометрического смысла
производной.
16.
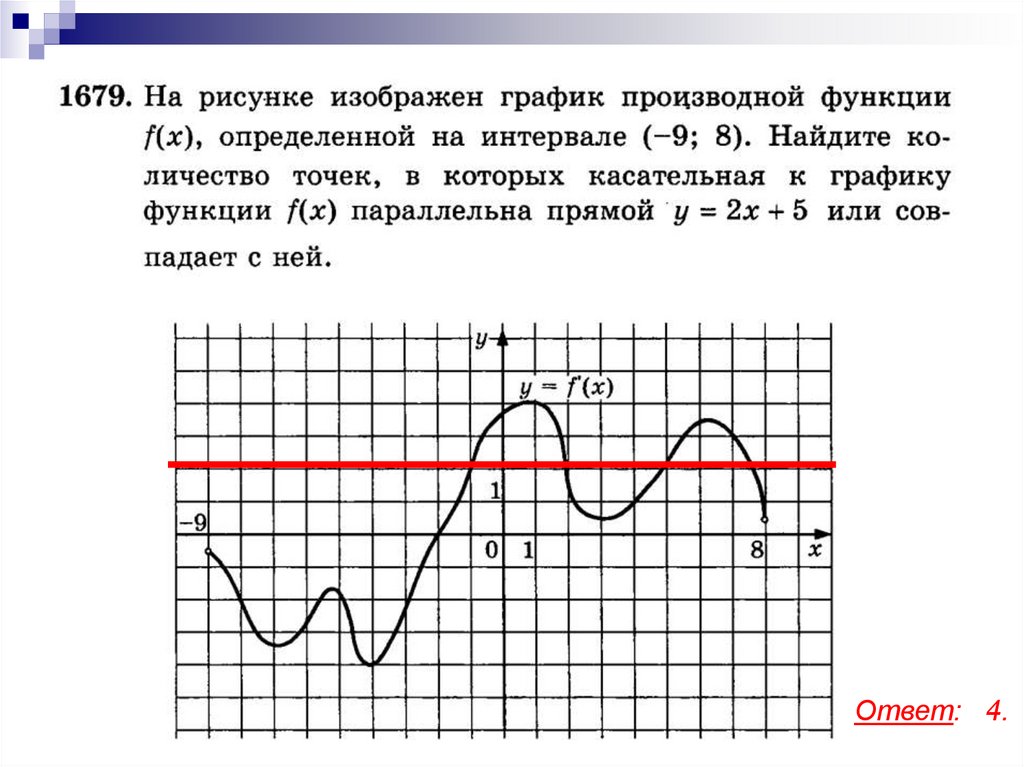
Ответ: 4.17.
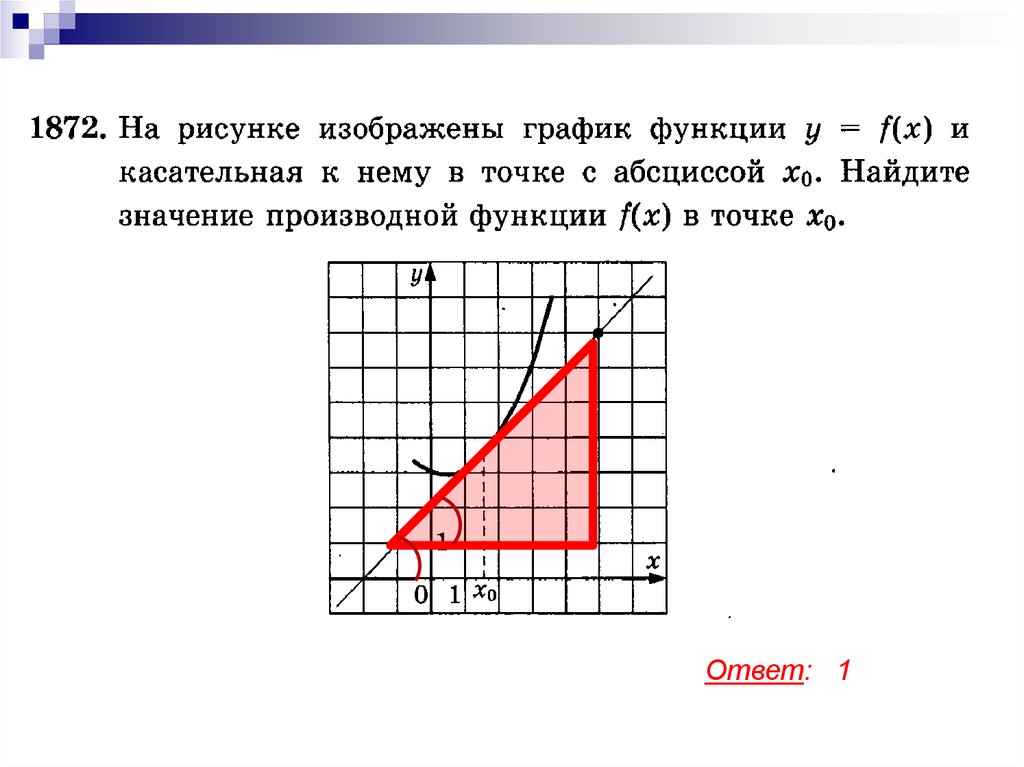
Ответ: 118.
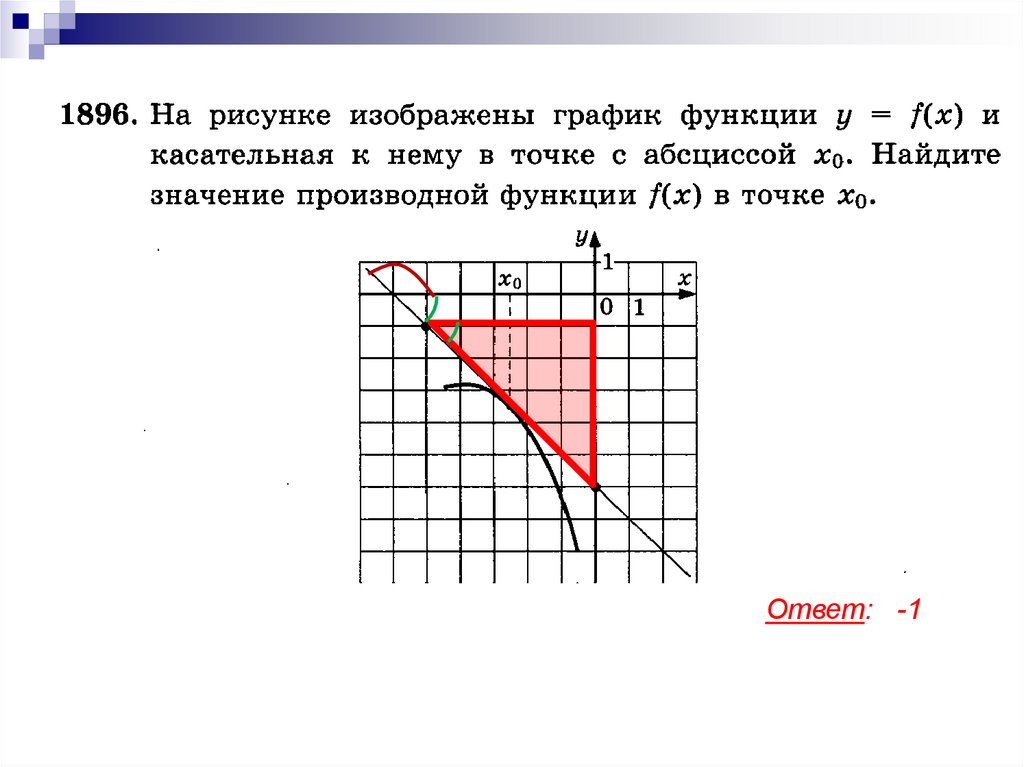
Ответ: -119.
Формулы дифференцированияС 0
х 1
kх m k
2
( х ) 2 х
1
1
2
х
х
1
х
2 х











 mathematics
mathematics








