Свойства равнобедренного треугольника

1.

Свойства равнобедренного
треугольника
Учитель математики ГБОУ лицей № 408
Сидоренкова Н.В.

2.

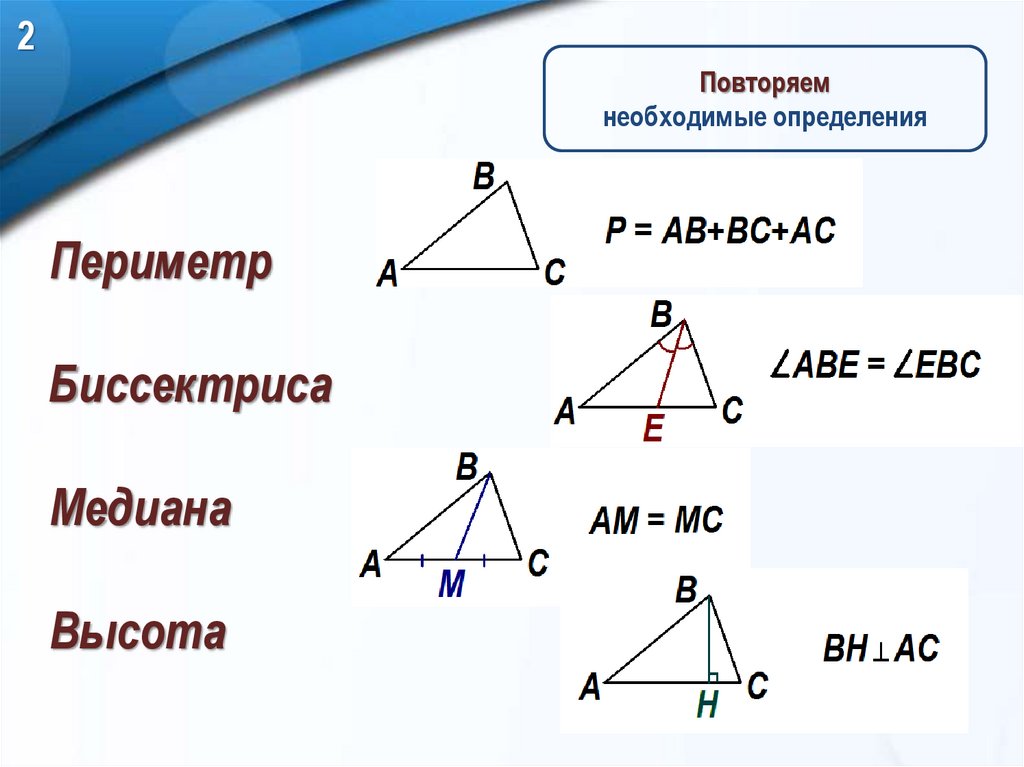
2
Повторяем
необходимые определения
Периметр
Биссектриса
Медиана
Высота

3.

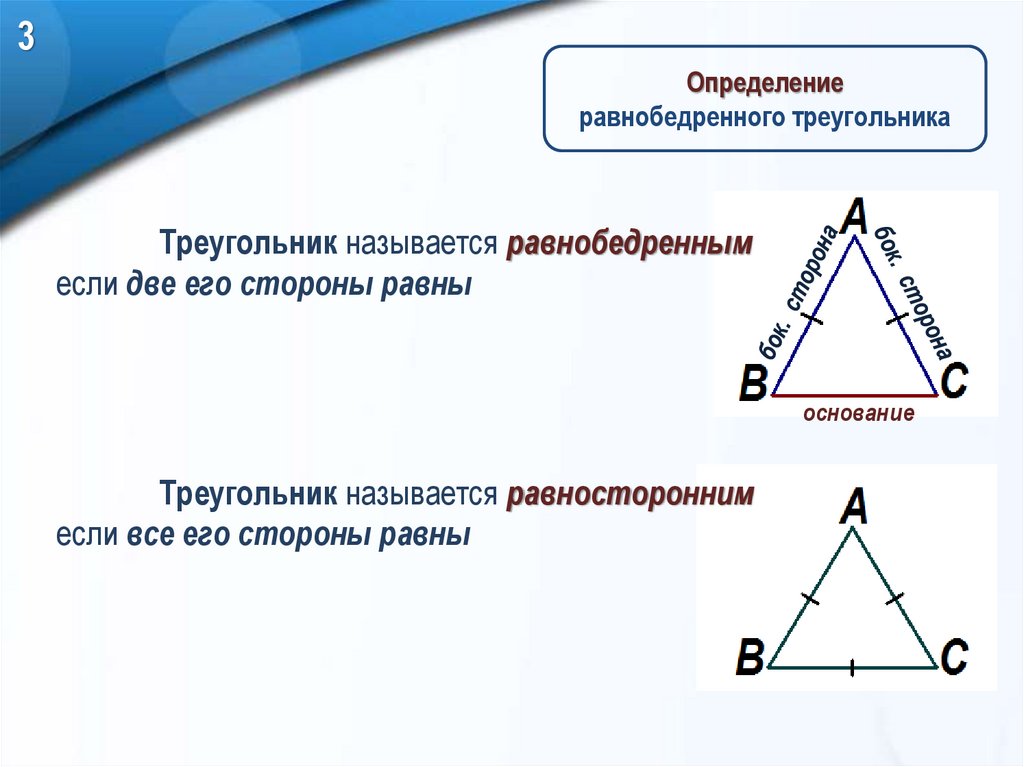
3
Определение
равнобедренного треугольника
Треугольник называется равнобедренным
если две его стороны равны
основание
Треугольник называется равносторонним
если все его стороны равны

4.

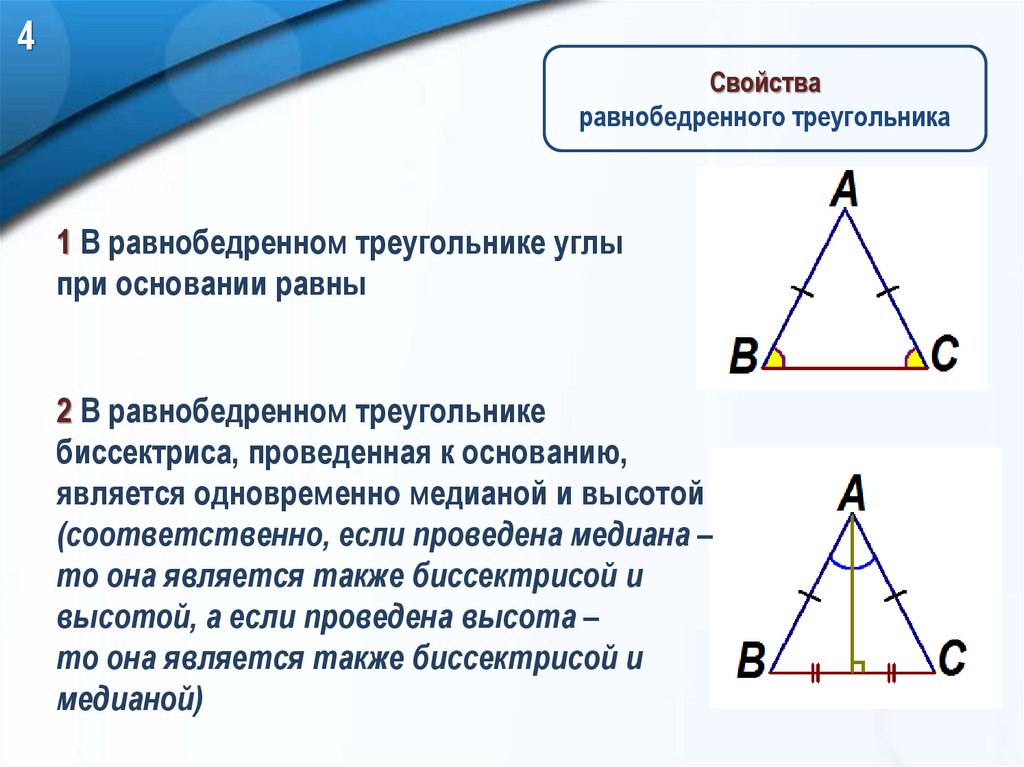
4
Свойства
равнобедренного треугольника
1 В равнобедренном треугольнике углы
при основании равны
2 В равнобедренном треугольнике
биссектриса, проведенная к основанию,
является одновременно медианой и высотой
(соответственно, если проведена медиана –
то она является также биссектрисой и
высотой, а если проведена высота –
то она является также биссектрисой и
медианой)

5.

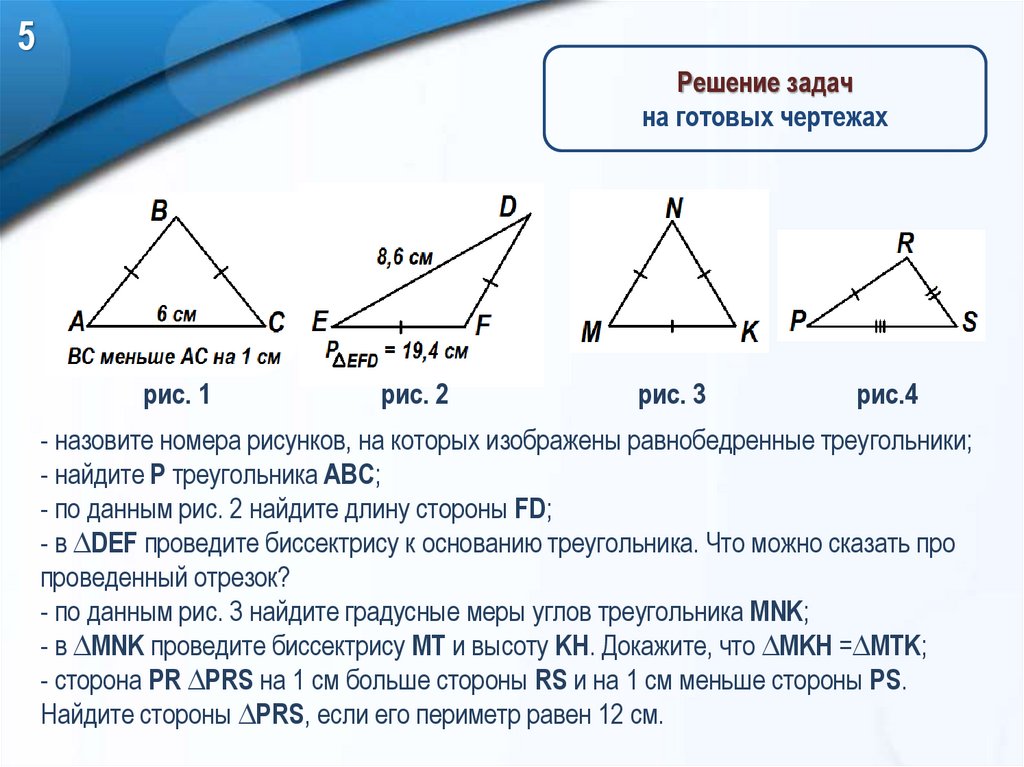
5
Решение задач
на готовых чертежах
рис. 1
рис. 2
рис. 3
рис.4
- назовите номера рисунков, на которых изображены равнобедренные треугольники;
- найдите P треугольника ABC;
- по данным рис. 2 найдите длину стороны FD;
- в ∆DEF проведите биссектрису к основанию треугольника. Что можно сказать про
проведенный отрезок?
- по данным рис. 3 найдите градусные меры углов треугольника MNK;
- в ∆MNK проведите биссектрису MT и высоту KH. Докажите, что ∆MKH =∆MTK;
- сторона PR ∆PRS на 1 см больше стороны RS и на 1 см меньше стороны PS.
Найдите стороны ∆PRS, если его периметр равен 12 см.

6.

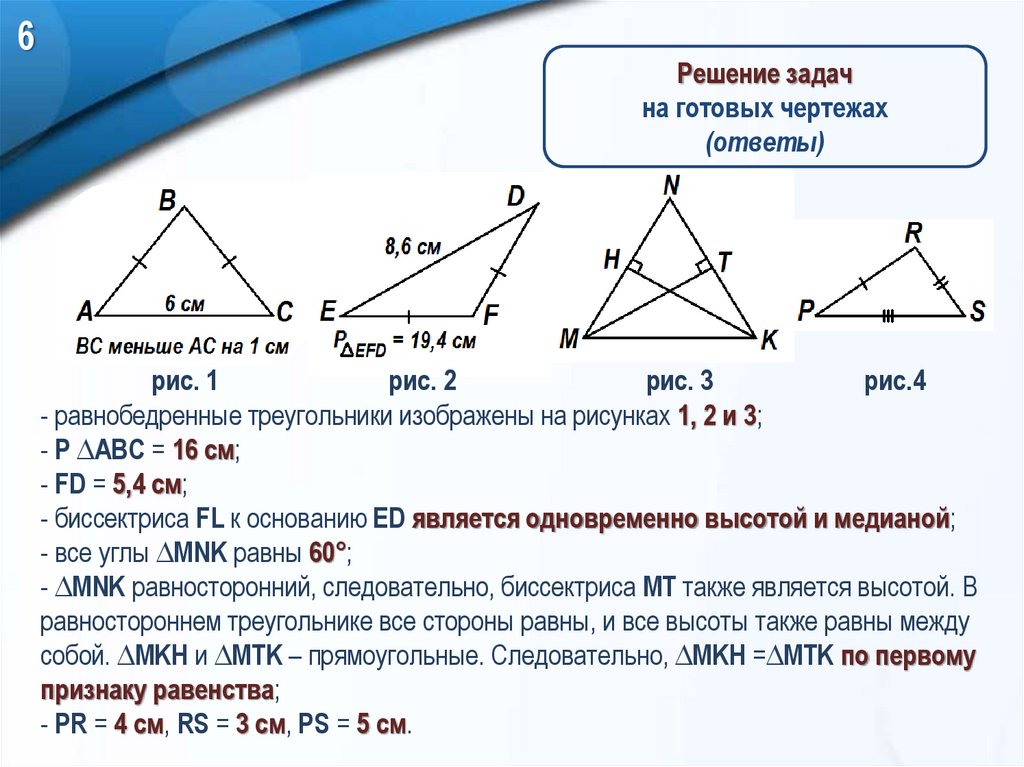
6
Решение задач
на готовых чертежах
(ответы)
рис. 1
рис. 2
рис. 3
рис.4
- равнобедренные треугольники изображены на рисунках 1, 2 и 3;
- P ∆ABC = 16 см;
- FD = 5,4 см;
- биссектриса FL к основанию ED является одновременно высотой и медианой;
- все углы ∆MNK равны 60°;
- ∆MNK равносторонний, следовательно, биссектриса MT также является высотой. В
равностороннем треугольнике все стороны равны, и все высоты также равны между
собой. ∆MKH и ∆MTK – прямоугольные. Следовательно, ∆MKH =∆MTK по первому
признаку равенства;
- PR = 4 см, RS = 3 см, PS = 5 см.

7.

7
Рефлексия
Я все понял и смогу помочь другим
Я понял, но не все. Остались вопросы
Я почти ничего не понял. Было трудно

8.

Спасибо за урок!